Intercept at constant angular speed
Storyboard 
Objects can intersect when they coincide in angle at the same moment. To achieve this, they must move from their respective initial angles with angular velocities that allow them to coincide in angle and time at the end of the journey.
ID:(1450, 0)
Intercept at constant angular speed
Storyboard 
Objects can intersect when they coincide in angle at the same moment. To achieve this, they must move from their respective initial angles with angular velocities that allow them to coincide in angle and time at the end of the journey.
Variables
Calculations
Calculations
Equations
In the case where the initial Angular Speed ($\omega_0$) is equal to the mean angular velocity ($\bar{\omega}$),
Therefore, with the difference of Angles ($\Delta\theta$), which is equal to the angle ($\theta$) divided by the initial Angle ($\theta_0$), we obtain:
And with the time elapsed ($\Delta t$), which is equal to the time ($t$) divided by the start Time ($t_0$), we obtain:
We can rewrite the equation for the mean angular velocity ($\bar{\omega}$) as:
This can be expressed as:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Solving for it, we get:
In the case where the initial Angular Speed ($\omega_0$) is equal to the mean angular velocity ($\bar{\omega}$),
Therefore, with the difference of Angles ($\Delta\theta$), which is equal to the angle ($\theta$) divided by the initial Angle ($\theta_0$), we obtain:
And with the time elapsed ($\Delta t$), which is equal to the time ($t$) divided by the start Time ($t_0$), we obtain:
We can rewrite the equation for the mean angular velocity ($\bar{\omega}$) as:
This can be expressed as:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Solving for it, we get:
As the mean Speed ($\bar{v}$) is with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$), equal to
and with the distance traveled in a time ($\Delta s$) expressed as an arc of a circle, and the radius ($r$) and the angle variation ($\Delta\theta$) are
and the definition of the mean angular velocity ($\bar{\omega}$) is
then,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Since the relationship is general, it can be applied for instantaneous values, resulting in
As the mean Speed ($\bar{v}$) is with the distance traveled in a time ($\Delta s$) and the time elapsed ($\Delta t$), equal to
and with the distance traveled in a time ($\Delta s$) expressed as an arc of a circle, and the radius ($r$) and the angle variation ($\Delta\theta$) are
and the definition of the mean angular velocity ($\bar{\omega}$) is
then,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Since the relationship is general, it can be applied for instantaneous values, resulting in
The definition of the mean angular velocity ($\bar{\omega}$) is considered as the angle variation ($\Delta\theta$),
and the time elapsed ($\Delta t$),
The relationship between both is defined as the mean angular velocity ($\bar{\omega}$):
The definition of the mean angular velocity ($\bar{\omega}$) is considered as the angle variation ($\Delta\theta$),
and the time elapsed ($\Delta t$),
The relationship between both is defined as the mean angular velocity ($\bar{\omega}$):
Examples
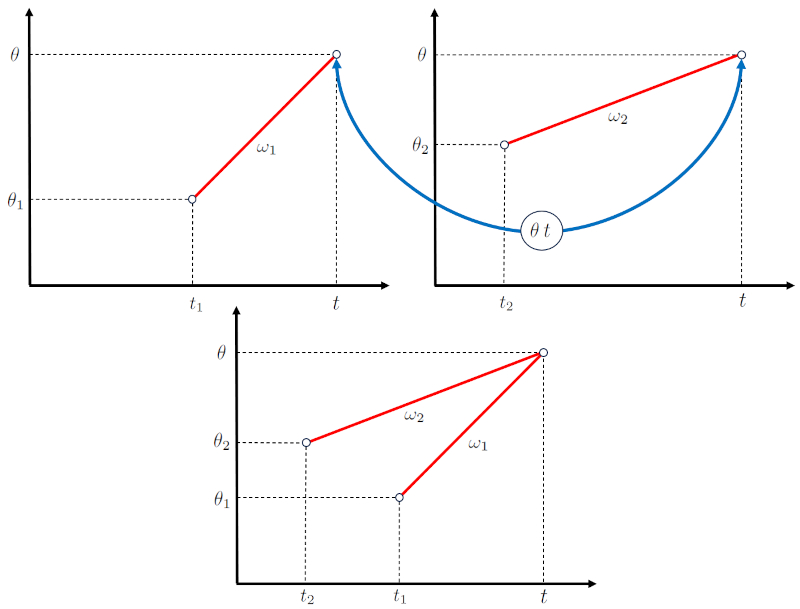
In the case of an intersection, two bodies are moving in such a way that they will meet at ERROR:10307,0 at time a intersection time ($t$).
To achieve this, each body:
• Begins its displacement at the initial time of first object ($t_1$) at the initial angle of the first body ($\theta_1$) with a angular velocity of body 1 ($\omega_1$).
• Begins its displacement at the initial time of second object ($t_2$) at the initial angle of the second body ($\theta_2$) with a angular velocity of body 2 ($\omega_2$).
These conditions must be met to achieve the intersection.
Thus, the angle over time diagrams can be overlaid as shown in the following representation:
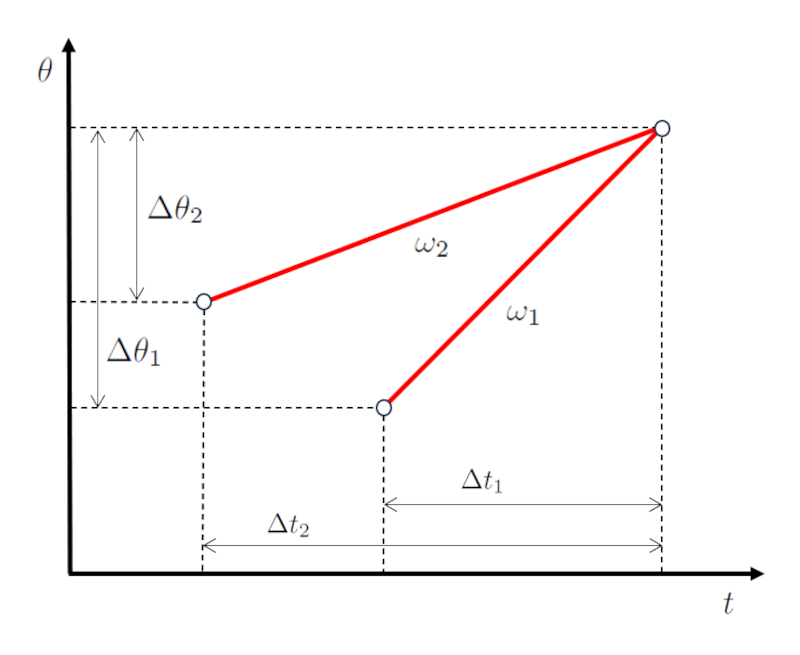
In the case of an intersection or collision between two objects, it's common for the angular velocity of body 1 ($\omega_1$) and the angular velocity of body 2 ($\omega_2$) to be configured such that they coincide.
This means that the angle traveled by the first body ($\Delta\theta_1$) and the travel time of first object ($\Delta t_1$) must result in a angular velocity of body 1 ($\omega_1$),
so that, with the angle traveled by the second body ($\Delta\theta_2$) and the travel time of second object ($\Delta t_2$), we get a angular velocity of body 2 ($\omega_2$),
so that they finally coincide in time and space (position):
In the case of a movement where two objects intersect, such as the angle of intersection ($\theta$) and the intersection time ($t$), it is common for both. Therefore, if for the first object, the initial time of first object ($t_1$) and the initial angle of the first body ($\theta_1$) with the angular velocity of body 1 ($\omega_1$) fulfill:
and for the second object, the initial time of second object ($t_2$) and the initial angle of the second body ($\theta_2$) with the angular velocity of body 2 ($\omega_2$) fulfill:
which is represented as:
To describe the rotation of an object, we need to determine the angle variation ($\Delta\theta$). This is achieved by subtracting the initial Angle ($\theta_0$) from the angle ($\theta$), which is reached by the object during its rotation:
To describe the rotation of an object, we need to determine the angle variation ($\Delta\theta$). This is achieved by subtracting the initial Angle ($\theta_0$) from the angle ($\theta$), which is reached by the object during its rotation:
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
To describe the motion of an object, we need to calculate the time elapsed ($\Delta t$). This magnitude is obtained by measuring the start Time ($t_0$) and the the time ($t$) of said motion. The duration is determined by subtracting the initial time from the final time:
In the case where the angular velocity is constant, the mean angular velocity ($\bar{\omega}$) coincides with the value of the initial Angular Speed ($\omega_0$), so
In this scenario, we can calculate the angle traveled as a function of time by recalling that it is associated with the difference between the current and initial angles, as well as the current and initial time. Therefore, the angle ($\theta$) is equal to the initial Angle ($\theta_0$), the initial Angular Speed ($\omega_0$), the time ($t$), and the start Time ($t_0$) as shown below:
The equation represents a straight line in angle-time space.
In the case where the angular velocity is constant, the mean angular velocity ($\bar{\omega}$) coincides with the value of the initial Angular Speed ($\omega_0$), so
In this scenario, we can calculate the angle traveled as a function of time by recalling that it is associated with the difference between the current and initial angles, as well as the current and initial time. Therefore, the angle ($\theta$) is equal to the initial Angle ($\theta_0$), the initial Angular Speed ($\omega_0$), the time ($t$), and the start Time ($t_0$) as shown below:
The equation represents a straight line in angle-time space.
To estimate the displacement of an object, it's necessary to know its the angular Speed ($\omega$) as a function of the time ($t$). Therefore, the the mean angular velocity ($\bar{\omega}$) is introduced, defined as the ratio between the angle variation ($\Delta\theta$) and the time elapsed ($\Delta t$).
To measure this, a system like the one shown in the image can be used:
To determine the average angular velocity, a reflective element is placed on the axis or on a disk with several reflective elements, and the passage is recorded to estimate the length of the arc $\Delta s$ and the angle associated with the radius $r$. Then the time difference when the mark passes in front of the sensor is recorded as $\Delta t$. The average angular velocity is determined by dividing the angle traveled by the time elapsed.
The equation that describes the average angular velocity is:
It should be noted that the average velocity is an estimation of the actual angular velocity. The main problem is that:
If the angular velocity varies during the elapsed time, the value of the average angular velocity can be very different from the average angular velocity.
Therefore, the key is:
Determine the velocity in a sufficiently short elapsed time to minimize its variation.
To estimate the displacement of an object, it's necessary to know its the angular Speed ($\omega$) as a function of the time ($t$). Therefore, the the mean angular velocity ($\bar{\omega}$) is introduced, defined as the ratio between the angle variation ($\Delta\theta$) and the time elapsed ($\Delta t$).
To measure this, a system like the one shown in the image can be used:
To determine the average angular velocity, a reflective element is placed on the axis or on a disk with several reflective elements, and the passage is recorded to estimate the length of the arc $\Delta s$ and the angle associated with the radius $r$. Then the time difference when the mark passes in front of the sensor is recorded as $\Delta t$. The average angular velocity is determined by dividing the angle traveled by the time elapsed.
The equation that describes the average angular velocity is:
It should be noted that the average velocity is an estimation of the actual angular velocity. The main problem is that:
If the angular velocity varies during the elapsed time, the value of the average angular velocity can be very different from the average angular velocity.
Therefore, the key is:
Determine the velocity in a sufficiently short elapsed time to minimize its variation.
If we divide the relationship between the distance traveled in a time ($\Delta s$) and the radius ($r$) by the angle variation ($\Delta\theta$),
and then divide it by the time elapsed ($\Delta t$), we obtain the relationship that allows us to calculate the speed ($v$) along the orbit, known as the tangential velocity, which is associated with the angular Speed ($\omega$):
If we divide the relationship between the distance traveled in a time ($\Delta s$) and the radius ($r$) by the angle variation ($\Delta\theta$),
and then divide it by the time elapsed ($\Delta t$), we obtain the relationship that allows us to calculate the speed ($v$) along the orbit, known as the tangential velocity, which is associated with the angular Speed ($\omega$):
ID:(1450, 0)