User:


Instant angular speed
Storyboard

The average angular velocity is defined by considering the angle traversed over a time interval, without taking into account any possible fluctuations in angular velocity.

To determine the angular velocity at a specific instant, it is necessary to consider an extremely small time interval, so that the angular velocity does not exhibit significant changes during that period.

Therefore, the instantaneous angular velocity is obtained by calculating the average angular velocity as the limit of a time interval approaching zero. From a mathematical standpoint, this is equivalent to taking the derivative of the angle with respect to time and represents the slope of the angle-time curve.

>Model

ID:(1447, 0)


Segment area angle traveled
Note

If we observe that the angular velocity $\omega$ is equal to the angle $\Delta\theta$ multiplied by the time $\Delta t$, we can state that the displacement is

$\Delta\theta = \omega\Delta t$



Since the product $\omega\Delta t$ represents the area under the curve of angular velocity versus time, and this area is also equal to the displacement traveled:

ID:(11417, 0)


Angle as an integral of angular velocity
Quote

The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of velocity between times $t_0$ and $t$ corresponds to the angle traveled between the initial position $\theta_0$ and $\theta$.

This can be expressed mathematically as:

$ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$



This relationship is shown graphically below:

This formula is useful for calculating the angle traveled by an object in situations where the velocity function is known. The integral of the velocity function provides a measure of the total displacement of the object between the two times $t_0$ and $t$, which can be used to calculate the angle traveled by the object by dividing the displacement by the radius of the circle. This concept is particularly useful in physics and engineering applications where rotational motion is involved.

ID:(11409, 0)


Tangential speed
Equation

If an object is subjected to a mode of maintaining a constant radius, it will rotate as indicated in the figure. Upon observing the figure, one would notice that the mass undergoes a translational motion with a tangential velocity that is equal to the radius times the angular velocity:

However, if the element connecting the object to the axis is cut, the object will continue to move tangentially in a straight line.

ID:(310, 0)


Instant angular speed
Description

The average angular velocity is defined by considering the angle traversed over a time interval, without taking into account any possible fluctuations in angular velocity. To determine the angular velocity at a specific instant, it is necessary to consider an extremely small time interval, so that the angular velocity does not exhibit significant changes during that period. Therefore, the instantaneous angular velocity is obtained by calculating the average angular velocity as the limit of a time interval approaching zero. From a mathematical standpoint, this is equivalent to taking the derivative of the angle with respect to time and represents the slope of the angle-time curve.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$\theta$
theta
Angle
rad
$\vec{\theta}$
&theta
Angle (vector)
rad
$\omega$
omega
Angular Speed
rad/s
$\vec{\omega}$
&omega
Angular Speed
rad/s
$\theta_0$
theta_0
Initial Angle
rad
$\omega$
omega
Instantaneous Angular Speed
rad/s
$r$
r
Radio
m
$\vec{r}$
&r
Radius (vector)
m
$\vec{v}$
&v
Speed (Vector)
m/s
$t_0$
t_0
Start Time
s
$v_t$
v_t
Tangent speed
m/s
$t$
t
Time
s

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

If we consider the angle covered as the angle variation ($\Delta\theta$) at time $t+\Delta t$ and at $t$:

$\Delta\theta = \theta(t+\Delta t)-\theta(t)$



and use the time elapsed ($\Delta t$), then, in the limit of infinitesimally short times:

$\omega=\displaystyle\frac{\Delta\theta}{\Delta t}=\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}\rightarrow lim_{\Delta t\rightarrow 0}\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}=\displaystyle\frac{d\theta}{dt}$

This last expression corresponds to the derivative of the angle function $\theta(t)$, which in turn is the slope of the graphical representation of that function over time.

(ID 3232)

Since the speed ($v$) is with the instantaneous Angular Speed ($\omega$) and the radio ($r$) equals:

$ v = r \omega $



we can calculate the speed (Vector) ($\vec{v}$) using the cross product with the axis unit vector, denoted as $\hat{n}$, and the radial unit vector, denoted as $\hat{r}$:

$\hat{t} = \hat{n} \times \hat{r}$



Therefore, if we define

$\vec{v}=v\hat{t}$

,

$\vec{r}=r\hat{r}$

and

$\vec{\omega}=\omega\hat{n}$

,

then we can express the velocity as

$\vec{v}=v\hat{t}=v\hat{n}\times\hat{r}=r\omega\hat{n}\times\hat{r}=\vec{\omega}\times\vec{r}$



meaning

$ \vec{v} = \vec{\omega} \times \vec{r} $

(ID 11597)

Examples


(ID 15412)

If we take a time $t$ with an angle $\theta(t)$ and observe a point at a future time $t+\Delta t$ with an angle $\theta(t+\Delta t)$, we can estimate the velocity as the angle traveled

$\theta(t+\Delta t)-\theta(t)$



in the time $\Delta t$.

$\omega\sim\displaystyle\frac{\theta(t+\Delta t)-\theta(t)}{\Delta t}$



As the value of time $\Delta t$ is reduced, the angular velocity takes on the role of the tangent to the position curve at that time:

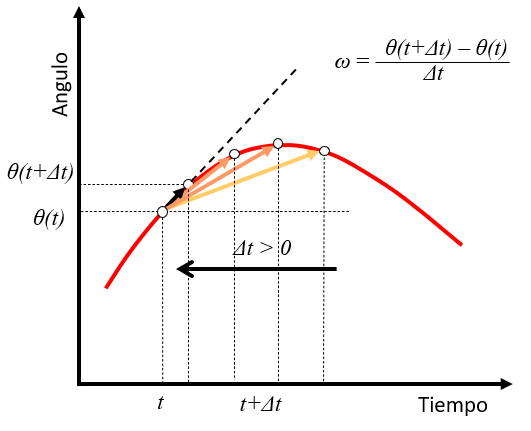
This generalizes what has already been seen for the case of constant angular velocity.

(ID 11407)

If we observe that the angular velocity $\omega$ is equal to the angle $\Delta\theta$ multiplied by the time $\Delta t$, we can state that the displacement is

$\Delta\theta = \omega\Delta t$



Since the product $\omega\Delta t$ represents the area under the curve of angular velocity versus time, and this area is also equal to the displacement traveled:

(ID 11417)

The integral of a function corresponds to the area under the curve that defines the function. Therefore, the integral of velocity between times $t_0$ and $t$ corresponds to the angle traveled between the initial position $\theta_0$ and $\theta$.

This can be expressed mathematically as:

$ \theta = \theta_0 +\displaystyle\int_{t_0}^t \omega d\tau$



This relationship is shown graphically below:

This formula is useful for calculating the angle traveled by an object in situations where the velocity function is known. The integral of the velocity function provides a measure of the total displacement of the object between the two times $t_0$ and $t$, which can be used to calculate the angle traveled by the object by dividing the displacement by the radius of the circle. This concept is particularly useful in physics and engineering applications where rotational motion is involved.

(ID 11409)

The orientation of the tangential velocity can be obtained using the right-hand rule. If the fingers point towards the axis of rotation and then are curled towards the position vector (radius), the thumb will point in the direction of the tangential velocity:

(ID 11599)

If an object is subjected to a mode of maintaining a constant radius, it will rotate as indicated in the figure. Upon observing the figure, one would notice that the mass undergoes a translational motion with a tangential velocity that is equal to the radius times the angular velocity:

However, if the element connecting the object to the axis is cut, the object will continue to move tangentially in a straight line.

(ID 310)


(ID 15423)

ID:(1447, 0)