User:
Turbulent flow through closed tubes
Storyboard 
For higher Reynolds numbers, the flow through a pipe becomes turbulent, leading to significant energy losses that must be accounted for in any modeling.
In the case of a closed pipe, the frictional losses are represented by the Darcy-Weisbach equation for pressure drop, or its equivalent head loss. These losses are modeled using a specific friction factor, which depends on the flow conditions and the characteristics of the pipe.
ID:(2111, 0)
Darcy-Weisbach equation
Concept
When modeling flow in a pipe, assuming that the energy density is conserved, we obtain Bernoullis equation. This equation describes the flow using the pressure difference ($\Delta p$) in terms of the liquid density ($\rho_w$), the mean Speed of Fluid ($v$), and the speed difference between surfaces ($\Delta v$):
| $ \Delta p = - \rho \bar{v} \Delta v $ |
In the case of turbulent flow, the mixing process acts as a friction that reduces the velocity gradient present in laminar flow between the center and the pipe walls. If we assume that this mixing effect can be modeled by a simple correction factor, we empirically arrive at the Darcy-Weisbach equation, which involves the darcy-Weisbach friction factor ($f_D$), the tube length ($\Delta L$), and the hydrodynamic diameter ($D_H$):
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
The factor the darcy-Weisbach friction factor ($f_D$) has been determined empirically for various flow conditions and is expressed as a function of the number of Reynold ($Re$).
ID:(15893, 0)
Moody diagram
Image
In 1944, Lewis Ferry Moody measured the Darcy-Weisbach friction factor as a function of the Reynolds number and the relative roughness of the wall, resulting in the creation of the following diagram:
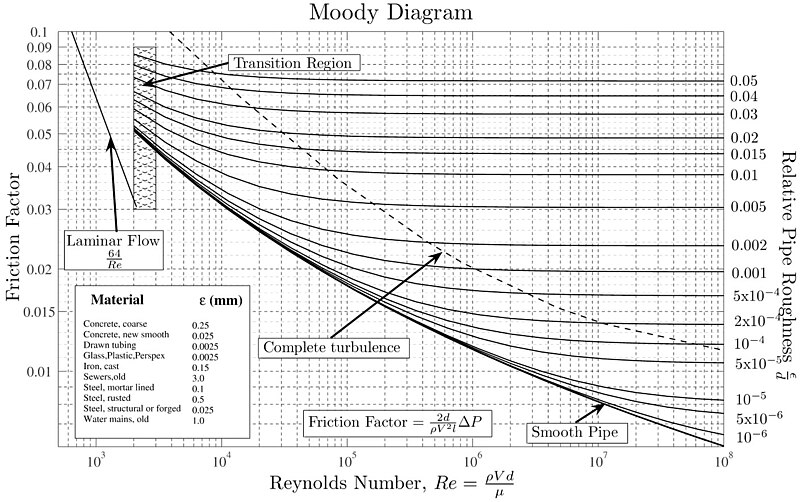
The relative roughness can be estimated by considering the size of surface irregularities (height of protrusions or depths of grooves) in relation to the hydraulic diameter.
Two distinct behaviors are observed:
• For Reynolds numbers below 2000, the Darcy-Weisbach friction factor depends solely on the Reynolds number, following a relationship of $64/Re$. This corresponds to the laminar flow regime.
• For Reynolds numbers above 2000, a behavior is observed that depends on both the Reynolds number and the relative roughness of the tube's surface.
ID:(14528, 0)
Hydraulic diameter
Concept
In the context of the Darcy-Weisbach equation, a hydrodynamic diameter ($D_H$) is used, which corresponds to a generalization of the traditional diameter of a circle. This allows us to consider a non-circular section and calculate an equivalent diameter based on the area of the section Tube ($S$) and its the perimeter ($P$) using the following formula:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
For a circular section, we obtain the traditional diameter of a circle as follows:
$D_H = \displaystyle\frac{4 S}{P} = \displaystyle\frac{4 \pi R^2}{2 \pi R} = 2R$
ID:(15894, 0)
Hydrodynamic perimeter in unfilled tube
Concept
The hydrodynamic perimeter ($P_H$) in a partially filled tube corresponds to the edges of the section in contact with the liquid, meaning the arc that touches both the wall of the tube and the surface:
Thus, it can generally be expressed as a function of the tube radius ($R$) and the depth in an unfilled tube ($h$) as:
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
For small flows, where the depth is significantly smaller than the radius, this simplifies the relationship between the cross-sectional area and the depth to:
| $ P_H = \sqrt{2^5 R h }$ |
ID:(15897, 0)
Depth of an unfilled tube
Concept
In a cylindrical tube, the depth is related to the flow as follows:
By integrating the section or Area ($S$), we can calculate how the surface area varies with the depth in an unfilled tube ($h$) through the integral over the radius up to the tube radius ($R$), which gives:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
For small flows, where the depth is significantly less than the radius, the relationship between the cross-sectional area and the depth simplifies considerably. Solving the depth equation gives:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
ID:(15896, 0)
Hydraulic radius
Concept
In the context of the Darcy-Weisbach friction factor, a hydraulic radius ($R_H$) is used, which is a generalization of the traditional radius of a circle. This allows us to calculate a diameter based on the area of the section Tube ($S$) and its perimeter in contact with the hydrodynamic perimeter ($P_H$), using the following formula:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
For a circular section, we can obtain the traditional hydraulic radius of a circle as follows:
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
ID:(15895, 0)
Surface of a disk
Equation
The surface of a disk ($S$) of ($$) is calculated as follows:
 $ S = \pi R ^2$ |
 $ S = \pi r ^2$ |
ID:(3804, 0)
Volume Flow and its Speed
Equation
A flux density ($j_s$) can be expressed in terms of the volume flow ($J_V$) using the section or Area ($S$) through the following formula:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Thus, the flow is a flux density ($j_s$), which is calculated using:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
ID:(4349, 0)
Reynold Number
Equation
The key criterion for determining whether a medium is laminar or turbulent is the Reynolds number, which compares the energy associated with inertia to that associated with viscosity. The former depends on the density ($\rho$), the mean Speed of Fluid ($v$), and the typical Dimension of the System ($R$), while the latter depends on the viscosity ($\eta$), defining it as:
| $ Re =\displaystyle\frac{ \rho_w R j_s }{ \eta }$ |
| $ Re =\displaystyle\frac{ \rho R v }{ \eta }$ |
ID:(3177, 0)
Depth of an unfilled tube
Equation
The depth in an unfilled tube ($h$) can be estimated when the liquid level is low, meaning that the level is much smaller than the radius of the tube, as a function of the section or Area ($S$) and the tube radius ($R$):
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
The section or Area ($S$) of the tube containing the liquid can be expressed as a function of the depth in an unfilled tube ($h$) by integrating over the radius up to the tube radius ($R$):
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
If we expand this expression in terms of the factor $h/R$ in the limit $h\ll R$, we obtain, to first order:
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
If we solve for the depth, we finally obtain:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
ID:(14541, 0)
Hydrodynamic perimeter in unfilled tube
Equation
The hydrodynamic perimeter ($P_H$) can be estimated from the depth in an unfilled tube ($h$) and the tube radius ($R$) using:
| $ P_H = \sqrt{2^5 R h }$ |
Since the angle between the radius at the edge of the liquid surface and the vertical can be calculated using the depth in an unfilled tube ($h$) and the tube radius ($R$) as:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
The corresponding arc is $R\phi$, so the total arc is:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
Similarly, half of the surface area can be determined using the Pythagorean theorem, which results in:
$\sqrt{2Rh - h^2}$
Therefore, the hydrodynamic perimeter ($P_H$) is expressed as:
$P_H = 2\sqrt{2Rh - h^2}+2R\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
In the limit of a small height, where $h\ll R$, this expression can be expanded, resulting in:
| $ P_H = \sqrt{2^5 R h }$ |
ID:(14542, 0)
Hydraulic radius
Equation
The hydraulic radius ($R_H$) can be calculated using the section Tube ($S$) and the hydrodynamic perimeter ($P_H$) through:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
ID:(14531, 0)
Hydraulic diameter
Equation
The hydrodynamic diameter ($D_H$) can be calculated from the section Tube ($S$) and the perimeter ($P$) using:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
ID:(14527, 0)
Solution for closed tube
Equation
The Colebrook-White equation for the case of a closed tube:
| $\displaystyle\frac{1}{\sqrt{ f_D }}=-2\log\left(\displaystyle\frac{\epsilon}{3.7 D_H}+\displaystyle\frac{2.51}{ Re \sqrt{ f_D }}\right)$ |
is an implicit equation used to determine the Darcy-Weisbach friction factor ($f_D$). To solve this equation, various approximations have been developed, which vary in complexity and accuracy. One of the most effective approximations that covers a wide range of Reynolds numbers $Re$ is the one proposed by S.E. Haaland:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
The original solution by S.E. Haaland is as follows:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/D_H}{3.7}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
It can be rearranged to obtain the expression for the Darcy-Weisbach friction factor $f_D$ as follows:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
ID:(14535, 0)
Darcy-Weisbach equation
Equation
The Darcy-Weisbach equation allows calculating the pressure difference ($\Delta p$) as a function of the liquid density ($\rho_w$), the hydrodynamic diameter ($D_H$), the darcy-Weisbach friction factor ($f_D$), the tube length ($\Delta L$), and the mean Speed of Fluid ($v$) through:
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
ID:(14526, 0)
Energy loss due to turbulence and friction
Equation
The Darcy-Weisbach equation allows calculating the pressure difference ($\Delta p$) as a function of the liquid density ($\rho_w$), the hydrodynamic diameter ($D_H$), the darcy-Weisbach friction factor ($f_D$), the tube length ($\Delta L$), and the mean Speed of Fluid ($v$) through:
| $ \Delta h_d = \displaystyle\frac{ \Delta L }{ 2 g D_H } f_D j_s ^2 $ |
ID:(15958, 0)