User:
Bases of special relativity
Storyboard
The behavior of particles at speeds close to the speed of light is different from what we know from classical mechanics. For this reason we must introduce the foundations of the so-called special relativity that Einstein formulated at the beginning of the last century.
ID:(1590, 0)
Temporal dilation: system at rest
Image
Let's consider a system A traveling horizontally at a velocity $v," where we have a device that emits light vertically. This light, after reflecting off a mirror, returns to the source:
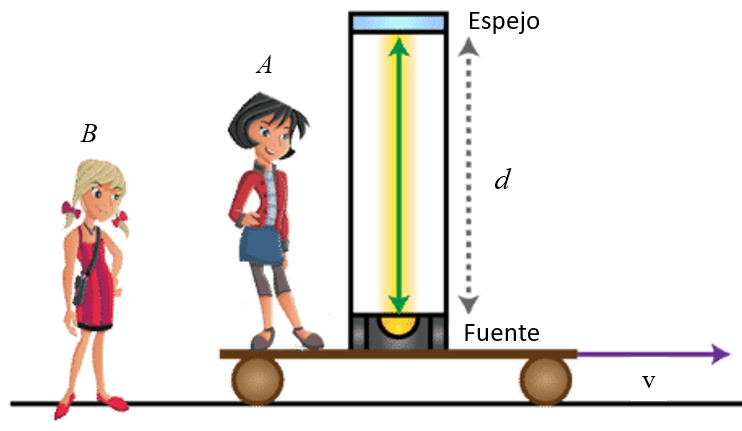
ID:(11777, 0)
Temporal dilation: time at rest
Equation
Let's assume a photon is emitted, and we measure the time it takes to travel from the source to the mirror, which we'll call $\Delta t_0$. If the length of the instrument is $d$ and the speed of light is $c," then the round trip time is:
 $ \Delta t_0 =\displaystyle\frac{ d }{ c }$ |
ID:(11778, 0)
Temporal dilation: time in motion
Image
For system A, the time it takes to cover the distance $d$ is equal to $\Delta t_0$, regardless of whether system A is in motion at a constant velocity $v":
This is because the concept of motion is relative and should always be considered with respect to a particular frame of reference. In this case, system B observes system A and claims that A is moving at a velocity of $v$. However, from the perspective of A, one could equally assert that A is at rest, and it's actually system B that is moving at a velocity of $-v$.
ID:(11779, 0)
Time dilation: from a system at rest
Image
When viewed from a system B at rest relative to system A, the time is estimated as $\Delta t_v$:
From B's point of view, the path that the photon travels includes not only the vertical distance $d$ but also an additional horizontal path of $v \Delta t_v$.
ID:(11780, 0)
Time dilation: time from a system at rest
Equation
From the perspective of system B, the distance traveled can be calculated using the Pythagorean theorem, considering the horizontal path covered as $v \Delta t_v$ and the vertical path as $d$:
$(v \Delta t_v)^2+d^2=(c \Delta t_v)^2$
Therefore, the time from the viewpoint of B is calculated as:
| $ \Delta t_v =\displaystyle\frac{ d }{\sqrt{ c ^2 - v ^2}}$ |
ID:(11781, 0)
Time dilation
Equation
Since the distance $d$ is orthogonal to the displacement, it remains independent of horizontal displacement, making it the same in the times of A:
| $ \Delta t_0 =\displaystyle\frac{ d }{ c }$ |
and B:
| $ \Delta t_v =\displaystyle\frac{ d }{\sqrt{ c ^2 - v ^2}}$ |
As a result, we can conclude that:
| $ \Delta t_v =\displaystyle\frac{ \Delta t_0 }{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
It follows that a
same event lasts for a different amount of time depending on whether it is observed from a system where the event is at rest or one that is in motion.
This phenomenon illustrates the concept of
time dilation, where the perceived time varies depending on the relative velocity between observers.
ID:(11782, 0)
Temporal dilation with the Lorentz factor
Equation
The time dilation, calculated using the equation
| $ \Delta t_v =\displaystyle\frac{ \Delta t_0 }{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
can be equivalently expressed as
| $ \gamma =\displaystyle\frac{1}{\sqrt{ 1 - \displaystyle\frac{ v ^2}{ c ^2}}}$ |
in the following manner:
| $ \Delta t_v = \gamma \Delta t_0 $ |
ID:(11784, 0)
Distance contraction
Image
The time dilation, coupled with the constraint that the speed of light remains constant in all systems, implies the existence of a contraction in distance.
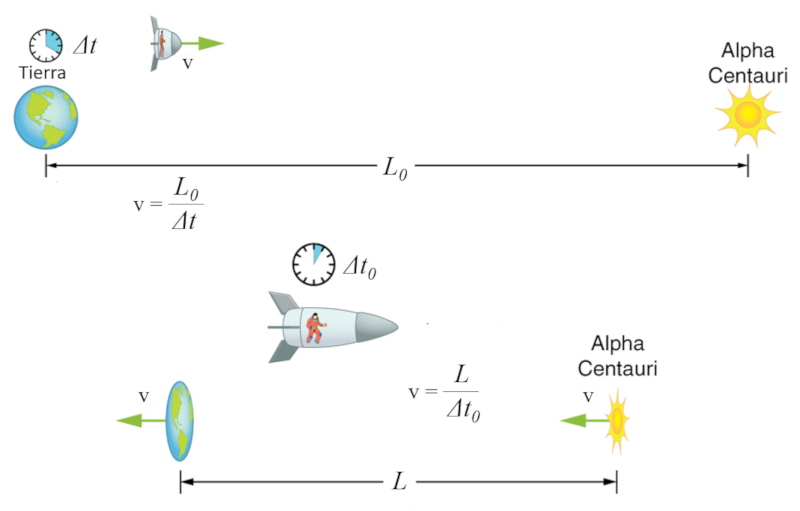
ID:(11785, 0)
Distance contraction, relationship
Equation
In system B, the distance covered by the moving system A is equal to $L_0$ with a velocity given by:
$v=\displaystyle\frac{ L_0 }{ \Delta t_v }$
From the perspective of system A, the distance covered is $L_v$ in a time interval $\Delta t_0$ with a velocity given by:
$v=\displaystyle\frac{ L_v }{ \Delta t_0 }$
Hence, with the time dilation described as
| $ \Delta t_v = \gamma \Delta t_0 $ |
we observe spatial contraction as
| $ L_v = \displaystyle\frac{1}{ \gamma } L_0 $ |
ID:(11786, 0)