Usuario:
Orbitales
Storyboard 
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
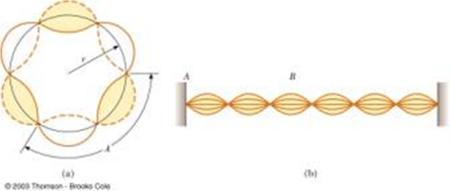
Modelo de De Broglie
Como el per metro de una rbita tiene un largo $2\pi r$, donde $r$ es el radio de la rbita, y la funci n de onda $\lambda$ que describe al electr n debe tener un largo de onda tal que un m ltiplo entero $n$ de esta debe ser igual al per metro:
El momento de la part cula $p$ es igual a la constante de Planck $h$ y el largo de onda $\lambda$ de la part cula:
El radio de Bohr depende de la carga del electr n $e$, la constante de campo $\epsilon_0$, la constante de Planck $h$, la masa del electr n $m$ y es
donde $a$ es el raio de Bohr.
En el modelo de Bohr el radio del $n$-esimo orbital depende del radio de Bohr
donde $a$ es el raio de Bohr.
La velocidad que define el modelo de Bohr depende de la carga el ctrica $e$, constante de campo $\epsilon_0$, constante de Planck $h$ y orbital $n$
ID:(1070, 0)