Sonore
Image 
Le son est décrit comme des fluctuations dans les densités des particules à l'intérieur du milieu à travers lequel il se propage. Ces fluctuations sont caractéristiques du son, qu'il se produise dans des gaz, des liquides ou des solides.
ID:(515, 0)
Génération de son
Noter 
Le son est produit lorsque une surface se déplace, augmentant ou diminuant le volume de gaz.
Dans le premier cas, les molécules environnantes occupent le nouvel espace, créant ainsi une zone de moindre densité d'air qui sera remplie par d'autres molécules voisines.
Dans le deuxième cas, les molécules environnantes sont comprimées, entraînant un déplacement vers des régions de plus faible densité.
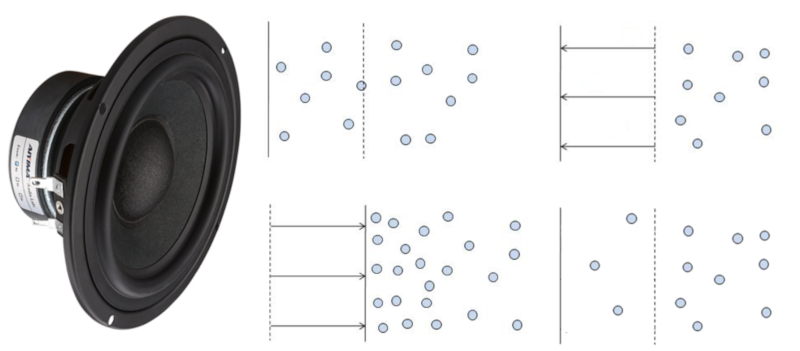
Ces deux changements entraînent la propagation de variations de densité, ce qui correspond à une onde sonore.
ID:(1670, 0)
Mouvement des molécules
Citation 
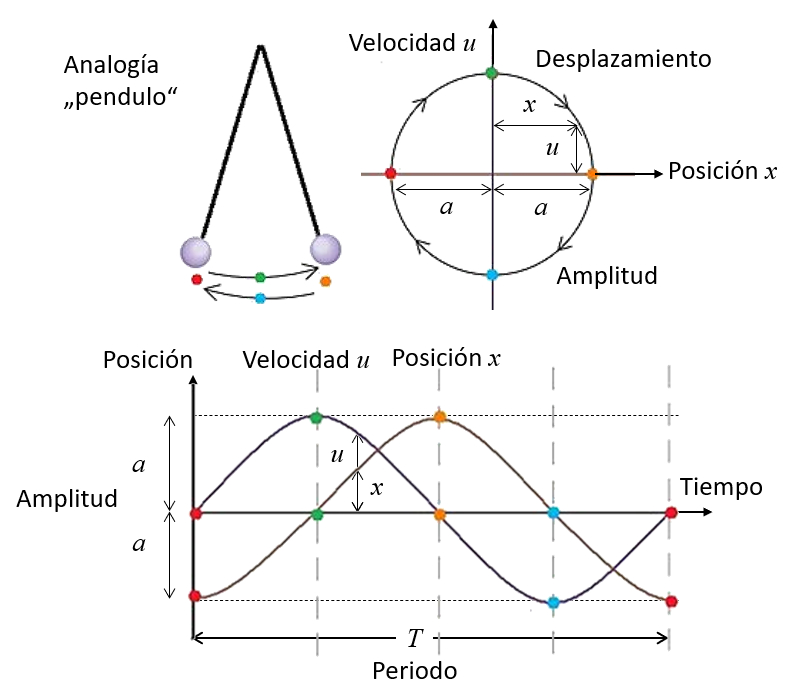
L'oscillation d'une molécule due à une onde sonore peut être décrite en termes de sa position et de sa vitesse.
Si les deux sont représentées comme des arêtes sur un graphique, on peut observer une trajectoire elliptique. Aux points extrêmes verticaux, la particule atteint une vitesse maximale, avec une extrémité étant positive (se déplaçant de gauche à droite) et l'autre extrémité étant négative (se déplaçant de droite à gauche). Les points extrêmes horizontaux représentent l'amplitude, où le point de gauche indique une valeur minimale et le point de droite indique une valeur positive.
De même, ces oscillations peuvent être représentées en fonction de le temps ($t$). Si l'on part d'un point où ERROR:5075 est initialement négatif et maximum, la vitesse est décrite par une fonction sinusoïdale, tandis que a temps ($x$) est décrite par une fonction cosinus qui a initialement une amplitude négatif. Cependant, ce choix est arbitraire, puisque le cycle peut démarrer à tout autre point, par exemple lorsque l'amplitude est initialement nulle, comme c'est le cas lorsque l'onde sonore arrive. Dans ce dernier cas, la position est modélisée avec une fonction sinusoïdale.
ID:(3187, 0)
Propagation du son
Exercer 
Le son est généré lorsqu'une surface se déplace, augmentant ou diminuant ainsi le volume d'un gaz environnant.
Une fois qu'une variation de densité/pression est créée, elle se propage à A vitesse des vagues ($c$) :
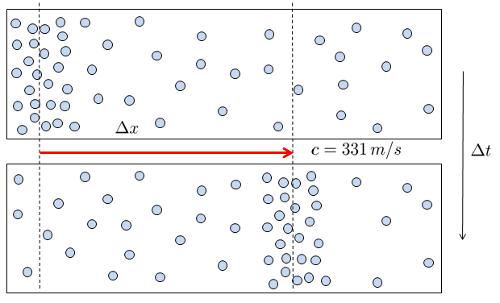
C'est pourquoi nous sommes capables d'entendre le son produit par un haut-parleur.
Il est important de reconnaître :
Le son nécessite un milieu dans lequel la densité/pression varie, que ce soit un gaz, un liquide ou un solide. Par conséquent, le son ne peut pas se propager dans le vide.
ID:(11795, 0)
Som
Description 
Le son correspond à des fluctuations de densité dans un gaz, un liquide ou un solide, capables de se propager dans le milieu. Le son existe dans tous les milieux gaz, liquide ou solide, la vitesse de propagation et latténuation variant selon le cas, bien que les modèles qui le décrivent soient généralement similaires.
Variables
Calculs
Calculs
Équations
(ID 3395)
(ID 3589)
A concentration molaire ($c$) avec le longueur d'onde sonore ($\lambda$) et a période ($T$) est exprim comme
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
et peut tre r crit avec a fréquence du son ($\nu$) comme
| $ \nu =\displaystyle\frac{1}{ T }$ |
ce qui nous donne la relation
| $ c = \lambda \nu $ |
(ID 12384)
Exemples
(ID 15457)
Le son est d crit comme des fluctuations dans les densit s des particules l'int rieur du milieu travers lequel il se propage. Ces fluctuations sont caract ristiques du son, qu'il se produise dans des gaz, des liquides ou des solides.
(ID 515)
Le son est produit lorsque une surface se d place, augmentant ou diminuant le volume de gaz.
Dans le premier cas, les mol cules environnantes occupent le nouvel espace, cr ant ainsi une zone de moindre densit d'air qui sera remplie par d'autres mol cules voisines.
Dans le deuxi me cas, les mol cules environnantes sont comprim es, entra nant un d placement vers des r gions de plus faible densit .

Ces deux changements entra nent la propagation de variations de densit , ce qui correspond une onde sonore.
(ID 1670)
L'oscillation d'une mol cule due une onde sonore peut tre d crite en termes de sa position et de sa vitesse.
Si les deux sont repr sent es comme des ar tes sur un graphique, on peut observer une trajectoire elliptique. Aux points extr mes verticaux, la particule atteint une vitesse maximale, avec une extr mit tant positive (se d pla ant de gauche droite) et l'autre extr mit tant n gative (se d pla ant de droite gauche). Les points extr mes horizontaux repr sentent l'amplitude, o le point de gauche indique une valeur minimale et le point de droite indique une valeur positive.
De m me, ces oscillations peuvent tre repr sent es en fonction de le temps ($t$). Si l'on part d'un point o ERROR:5075 est initialement n gatif et maximum, la vitesse est d crite par une fonction sinuso dale, tandis que a temps ($x$) est d crite par une fonction cosinus qui a initialement une amplitude n gatif. Cependant, ce choix est arbitraire, puisque le cycle peut d marrer tout autre point, par exemple lorsque l'amplitude est initialement nulle, comme c'est le cas lorsque l'onde sonore arrive. Dans ce dernier cas, la position est mod lis e avec une fonction sinuso dale.

(ID 3187)
Le son est g n r lorsqu'une surface se d place, augmentant ou diminuant ainsi le volume d'un gaz environnant.
Une fois qu'une variation de densit /pression est cr e, elle se propage a vitesse des vagues ($c$) :

C'est pourquoi nous sommes capables d'entendre le son produit par un haut-parleur.
Il est important de reconna tre :
Le son n cessite un milieu dans lequel la densit /pression varie, que ce soit un gaz, un liquide ou un solide. Par cons quent, le son ne peut pas se propager dans le vide.
(ID 11795)
(ID 15452)
Le mouvement moyen g n r par l'onde sonore correspond une oscillation autour de la position d'origine de la mol cule.
Cette oscillation peut tre d crite l'aide d'une fonction trigonom trique impliquant une amplitude $a$, une fr quence angulaire $\omega$ et le temps $t$.
L'oscillation est d crite de la mani re suivante :
| $ x = a \cos( \omega t )$ |
(ID 3392)
A fréquence du son ($\nu$) correspond au nombre de fois qu'une oscillation se produit en une seconde. A période ($T$) repr sente le temps n cessaire une seule oscillation. Par cons quent, le nombre d'oscillations par seconde est :
| $ \nu =\displaystyle\frac{1}{ T }$ |
La fr quence est indiqu e en Hertz (Hz).
(ID 4427)
Si nous observons le diagramme de vitesse par rapport la position, nous pouvons interpr ter l'oscillation comme un mouvement circulaire dans ce diagramme. Dans ce cas, nous pouvons estimer ERROR:5715 comme le p rim tre, qui est la distance parcourue divis e par le temps coul , qui est a période ($T$). Si ERROR:5075 est le rayon, alors avec a fréquence angulaire ($\omega$) :
$u=\displaystyle\frac{2\pi a}{T}=a\omega$
Cela signifie que ERROR:5715 est :
| $ u = a \omega $ |
(ID 3395)
A vitesse des vagues ($c$) est une vitesse, ce qui signifie qu'elle est gale une longueur, comme a longueur donde ($\lambda$), divis e par le temps qu'une oscillation met avancer, c'est- -dire ERROR:9741. Par cons quent, nous avons :
| $ c = \displaystyle\frac{ \lambda }{ T }$ |
(ID 12378)
A concentration molaire ($c$) est une vitesse, ce qui signifie qu'elle est gale une longueur, comme le longueur d'onde sonore ($\lambda$), divis e par le temps qu'une oscillation met avancer. Comme l'inverse du temps est a fréquence du son ($\nu$), nous avons donc :
| $ c = \lambda \nu $ |
(ID 12384)
(ID 3589)
ID:(385, 0)
