Utilisateur:
Courants parallèles
Définition 
Lorsque deux courants sont autorisés à circuler de manière parallèle, on observe une force attractive entre les fils.
Il est important de rappeler que les courants sont composés d'électrons en mouvement, et les électrons se repoussent naturellement en raison de leurs charges négatives. Cependant, lorsque ces charges sont en mouvement, cette force répulsive se transforme en une force attractive, ce qui entraîne l'observation d'une attraction entre les conducteurs chargés négativement.
ID:(11772, 0)
Courants parallèles opposés
Image
Lorsque deux courants circulent de manière parallèle mais en sens opposé, on observe une force répulsive entre les fils.
En comparant cette expérience à celle où le flux est parallèle mais circule dans la même direction, la différence clé réside dans la présence d'une vitesse relative dans le dernier cas.
ID:(11773, 0)
Courants parallèles, le champ n'est pas électrique
Noter
Si une plaque métallique est placée entre les deux conducteurs, aucun effet notable n'est observé :
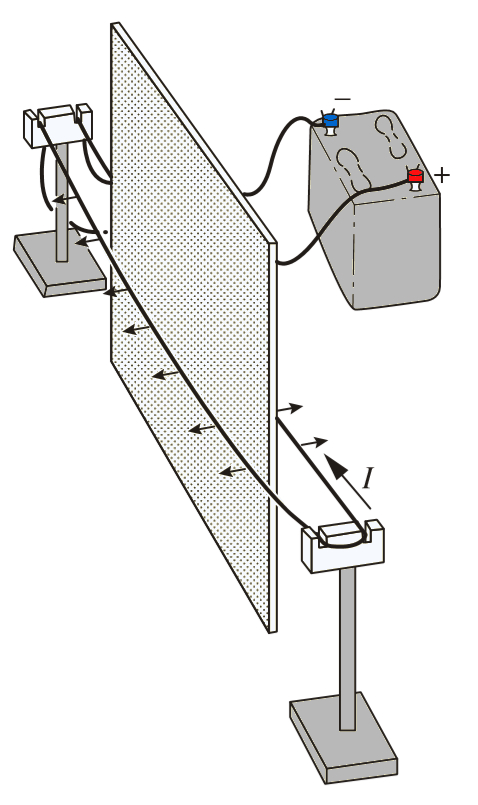
Par conséquent, nous en concluons que le champ généré ne correspond pas à un champ électrique traditionnel.
ID:(11774, 0)
Effet du courant sur une boussole
Citation
Lorsqu'une boussole est exposée à un courant électrique, les observations suivantes peuvent être faites :
En résumé, l'aiguille de la boussole :
• ne tourne pas s'il n'y a pas de courant électrique présent
• tourne lorsqu'il y a un flux de courant électrique
• si la direction du flux de courant électrique est inversée, la rotation de l'aiguille est également inversée.
ID:(11775, 0)
Détection du champ magnétique généré
Exercer
Lorsque l'on explore l'espace autour d'un fil avec une boussole, on constate que le courant électrique induit la présence d'un champ magnétique :
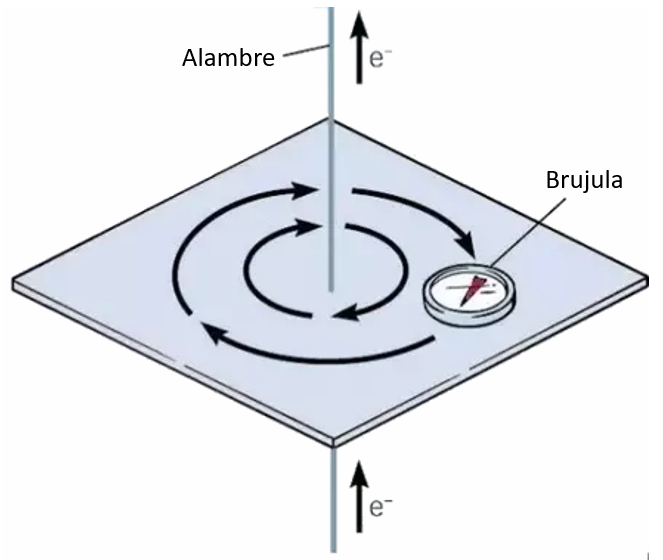
C'est pourquoi des fils parallèles peuvent soit s'attirer, soit se repousser en fonction de la direction du courant électrique. La clé réside dans le fait que :
Le courant électrique génère un champ magnétique, et ce champ magnétique exerce une force sur les charges en mouvement.
ID:(11776, 0)
Dynamique des particules
Description
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Exemples
A force ($F$), qui g n re a densité de flux magnétique ($B$) sur a charge ($q$), se d pla ant sous un angle entre la vitesse et le champ magnétique ($\theta$) avec a vitesse ($v$), sexprime comme suit :
| $ F = q v B \sin \theta $ |
(ID 3873)
L' quation du mouvement r sulte de l' quilibre entre la force g n r e par a densité de flux magnétique ($B$) agissant sur a charge ($q$) et a masse molaire ($m$), qui se d place avec a vitesse des particules ($v$) Le radio ($r$). Cette relation s'exprime comme suit :
| $ m \displaystyle\frac{ v ^2}{ r }= q v B $ |
(ID 3229)
L'orbite un rayon de giration des particules dans un champ magnétique ($r$) d pend de a masse molaire ($m$), a vitesse ($v$), a charge ($Q$) et a densité de flux magnétique ($B$), et est d crite par la relation suivante :
| $ r =\displaystyle\frac{ m v }{ q B }$ |
(ID 3874)
A vitesse angulaire ($\omega$) est d riv de a charge ($q$), a densité de flux magnétique ($B$) et a masse molaire ($m$), en utilisant la relation suivante :
| $ \omega =\displaystyle\frac{ q B }{ m }$ |
(ID 10058)
ID:(818, 0)