Gliding
Storyboard 
If the object (airplane / bird) maintains a slightly negative angle of attack, it can make part of the lifting force contribute to boost by countering the resistance. On the average that the remaining lift is not much less than the force of gravity, the object is long maintained in the air. You can talk about an extremely slow controlled descent or glide.
ID:(466, 0)
Glide
Description 
One method of flying is known as gliding. In this technique, the wings are used both for propulsion and to remain airborne. To achieve this, it is necessary to adjust the wing's angle of attack in a way that the lift force counteracts gravity. As a result, gliding becomes a controlled descent where the descent is used to generate lift and thereby reduce speed in a controlled manner.
ID:(1171, 0)
Flying forces
Description 
The key to gliding is to tilt the aircraft or bird forward, in other words, to have a negative angle represented by ERROR:6121,0. With this negative angle, the the lift force ($F_L$) vector points upward and forward instead of backward. This results in a pulling force rather than the resistance force ($F_W$), propelling the aircraft or bird and generating speed, which, in turn, creates the necessary lift.
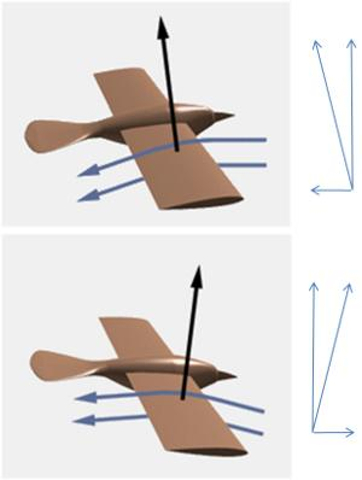
This mechanism allows for flight, but it's essential to understand that it's essentially a slow and controlled descent since it doesn't achieve a completely vertical a lift force ($F_L$) to counteract its own weight. Therefore, it's necessary to take the glider to high altitudes or allow the bird to gain initial height through its own propulsion. Afterward, both seek ascending air currents that enable them to glide within an updraft stronger than the glider's descent rate. This way, they can remain in flight for extended periods without the need to land.
ID:(7044, 0)
Glide angle
Description 
Similarly to how the angle of attack of a wing ($\alpha$) is defined as the angle between the wing's centerline and the horizon, its negative counterpart can be defined as the glide angle ($\phi$).

Jonker JS3 Rapture sailplane glider (Air Cargo Week)
ID:(7047, 0)
Forces in gliding
Description 
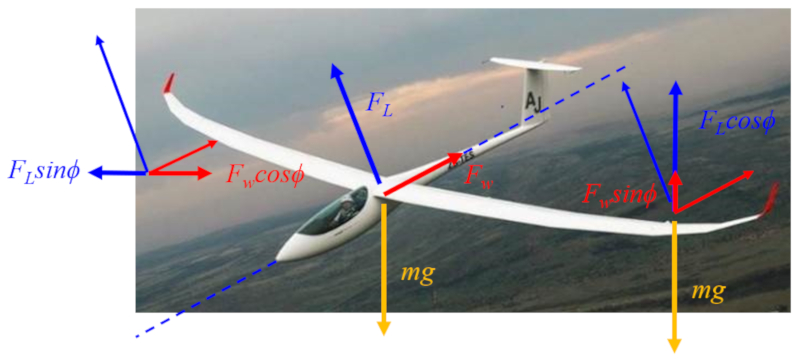
When it comes to forces, we have the following actions:
• the lift force ($F_L$) acts perpendicularly to the aircraft or bird's axis.
• the resistance force ($F_W$) acts along the aircraft or bird's axis.
• the gravitational force ($F_g$) ($mg$) acts vertically.
These three forces are depicted at the center of the diagram:
Jonker JS3 Rapture sailplane glider (Air Cargo Week)
On the left side, you can see the horizontal component, where lift counters the drag, acting as thrust.On the right side, the vertical components are visible, where both aerodynamic forces (lift and drag) oppose the weight acting on the center of mass.Although the forces balance each other out, the glider descends because its flight direction is determined by the glide angle.
ID:(7046, 0)
Angulo de Planeo
Description 
The angle of planning is that angle of inclination in which the horizontal component of the traction force counteracts the horizontal friction while the sum of the support and friction in the vertical direction counteracts the force of gravity. This situation allows a descent with an angle equal to the gliding angle that can be small allowing a very slow descent.
ID:(1586, 0)
Resistance force in gliding
Concept 
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
and in the horizontal direction is:
| $ F_L \sin \phi = F_w \cos \phi $ |
This allows us to eliminate the lift force ($F_L$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
the resistance force ($F_W$) should be:
| $ F_W = m g \sin \phi $ |
ID:(15769, 0)
Lifting force in gliding
Concept 
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
and in the horizontal direction:
| $ F_L \sin \phi = F_w \cos \phi $ |
This allows us to eliminate the resistance force ($F_W$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Therefore, the lift force ($F_L$) is:
| $ F_L = m g \cos\phi $ |
ID:(15770, 0)
Glide angle
Concept 
Let's consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$). With these forces, the lift force is calculated as:
| $ F_L = m g \cos\phi $ |
and the drag force as:
| $ F_W = m g \sin \phi $ |
We can determine the glide angle ($\phi$) by dividing the lift force ($F_L$) by the resistance force ($F_W$), resulting in:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Where the resistance force ($F_W$) is calculated using the equation:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
with the total object profile ($S_p$) and the coefficient of resistance ($C_W$). Similarly, the lift force ($F_L$) is calculated as:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
with the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$).
With both forces, we can determine the necessary angle of attack for gliding as:
| $ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$ |
ID:(15771, 0)
Gliding
Model 
If the object (airplane / bird) maintains a slightly negative angle of attack, it can make part of the lifting force contribute to boost by countering the resistance. On the average that the remaining lift is not much less than the force of gravity, the object is long maintained in the air. You can talk about an extremely slow controlled descent or glide.
Variables
Calculations
Calculations
Equations
The lift force ($F_L$), along with the wing span ($L$), the density ($\rho$), the wing top speed factor ($c_t$), the wing bottom speed factor ($c_b$), the upper wing length ($l_t$), the bottom wing length ($l_b$), and the speed with respect to the medium ($v$), is found in
| $ F_L = \rho L ( c_b l_b - c_t l_t ) v ^2$ |
If we consider the surface that generates lift ($S_w$), given by the wing span ($L$), the upper wing length ($l_t$), and the bottom wing length ($l_b$),
| $ S_w = \displaystyle\frac{1}{2} L ( l_t + l_b )$ |
and for the coefficient of lift ($C_L$), defined as
| $ C_L = 4\displaystyle\frac{ c_t l_t - c_b l_b }{ l_t + l_b }$ |
we obtain
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
(ID 4417)
Similarly to how the equation for the lift force ($F_L$) was derived using the density ($\rho$), the coefficient of lift ($C_L$), the surface that generates lift ($S_w$), and the speed with respect to the medium ($v$)
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
in this analogy, what corresponds to the surface that generates lift ($S_w$) will be equivalent to the total object profile ($S_p$) and the coefficient of lift ($C_L$) to the coefficient of resistance ($C_W$), thus the resistance force ($F_W$) is calculated:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
The drag coefficient is measured and, in turbulent flows over aerodynamic bodies, values are generally found around 0.4.
(ID 4418)
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
and in the horizontal direction:
| $ F_L \sin \phi = F_w \cos \phi $ |
This allows us to eliminate the resistance force ($F_W$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Therefore, the lift force ($F_L$) is:
| $ F_L = m g \cos\phi $ |
(ID 4421)
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
and in the horizontal direction is:
| $ F_L \sin \phi = F_w \cos \phi $ |
This allows us to eliminate the lift force ($F_L$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
the resistance force ($F_W$) should be:
| $ F_W = m g \sin \phi $ |
(ID 4422)
Let's consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$). With these forces, the lift force is calculated as:
| $ F_L = m g \cos\phi $ |
and the drag force as:
| $ F_W = m g \sin \phi $ |
We can determine the glide angle ($\phi$) by dividing the lift force ($F_L$) by the resistance force ($F_W$), resulting in:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Where the resistance force ($F_W$) is calculated using the equation:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
with the total object profile ($S_p$) and the coefficient of resistance ($C_W$). Similarly, the lift force ($F_L$) is calculated as:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
with the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$).
With both forces, we can determine the necessary angle of attack for gliding as:
| $ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$ |
(ID 4423)
Examples
(ID 15177)
One method of flying is known as gliding. In this technique, the wings are used both for propulsion and to remain airborne. To achieve this, it is necessary to adjust the wing's angle of attack in a way that the lift force counteracts gravity. As a result, gliding becomes a controlled descent where the descent is used to generate lift and thereby reduce speed in a controlled manner.
(ID 1171)
The key to gliding is to tilt the aircraft or bird forward, in other words, to have a negative angle represented by ERROR:6121,0. With this negative angle, the the lift force ($F_L$) vector points upward and forward instead of backward. This results in a pulling force rather than the resistance force ($F_W$), propelling the aircraft or bird and generating speed, which, in turn, creates the necessary lift.

This mechanism allows for flight, but it's essential to understand that it's essentially a slow and controlled descent since it doesn't achieve a completely vertical a lift force ($F_L$) to counteract its own weight. Therefore, it's necessary to take the glider to high altitudes or allow the bird to gain initial height through its own propulsion. Afterward, both seek ascending air currents that enable them to glide within an updraft stronger than the glider's descent rate. This way, they can remain in flight for extended periods without the need to land.
(ID 7044)
Similarly to how the angle of attack of a wing ($\alpha$) is defined as the angle between the wing's centerline and the horizon, its negative counterpart can be defined as the glide angle ($\phi$).

Jonker JS3 Rapture sailplane glider (Air Cargo Week)
(ID 7047)
When it comes to forces, we have the following actions:
• the lift force ($F_L$) acts perpendicularly to the aircraft or bird's axis.
• the resistance force ($F_W$) acts along the aircraft or bird's axis.
• the gravitational force ($F_g$) ($mg$) acts vertically.
These three forces are depicted at the center of the diagram:

Jonker JS3 Rapture sailplane glider (Air Cargo Week)
On the left side, you can see the horizontal component, where lift counters the drag, acting as thrust.On the right side, the vertical components are visible, where both aerodynamic forces (lift and drag) oppose the weight acting on the center of mass.Although the forces balance each other out, the glider descends because its flight direction is determined by the glide angle.
(ID 7046)
The angle of planning is that angle of inclination in which the horizontal component of the traction force counteracts the horizontal friction while the sum of the support and friction in the vertical direction counteracts the force of gravity. This situation allows a descent with an angle equal to the gliding angle that can be small allowing a very slow descent.
(ID 1586)
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
and in the horizontal direction is:
| $ F_L \sin \phi = F_w \cos \phi $ |
This allows us to eliminate the lift force ($F_L$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
the resistance force ($F_W$) should be:
| $ F_W = m g \sin \phi $ |
(ID 15769)
If we consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$), the force during gliding in the vertical direction is:
| $ F_L \cos \phi + F_w \sin \phi = m g $ |
and in the horizontal direction:
| $ F_L \sin \phi = F_w \cos \phi $ |
This allows us to eliminate the resistance force ($F_W$), resulting in:
$F_L=F_W\displaystyle\frac{\cos\phi}{\sin\phi} \rightarrow F_W(\sin^2\phi+\cos^2\phi)=mg\sin\phi$
Therefore, the lift force ($F_L$) is:
| $ F_L = m g \cos\phi $ |
(ID 15770)
Let's consider the lift force ($F_L$), the resistance force ($F_W$), the body mass ($m$), the gravitational Acceleration ($g$), and the glide angle ($\phi$). With these forces, the lift force is calculated as:
| $ F_L = m g \cos\phi $ |
and the drag force as:
| $ F_W = m g \sin \phi $ |
We can determine the glide angle ($\phi$) by dividing the lift force ($F_L$) by the resistance force ($F_W$), resulting in:
$\tan\phi=\displaystyle\frac{F_W}{F_L}$
Where the resistance force ($F_W$) is calculated using the equation:
| $ F_W =\displaystyle\frac{1}{2} \rho S_p C_W v ^2$ |
with the total object profile ($S_p$) and the coefficient of resistance ($C_W$). Similarly, the lift force ($F_L$) is calculated as:
| $ F_L =\displaystyle\frac{1}{2} \rho S_w C_L v ^2$ |
with the surface that generates lift ($S_w$) and the coefficient of lift ($C_L$).
With both forces, we can determine the necessary angle of attack for gliding as:
| $ \tan \phi =\displaystyle\frac{ S_p C_w }{ S_w C_L }$ |
(ID 15771)
(ID 15190)
ID:(466, 0)
