User:


Flow of an incompressible liquid
Storyboard

When a liquid is in motion, we refer to it as flow, and its measurement is based on the volume that passes through a section in a given period of time. Assuming that the volume moves without deformation, the velocity at which the liquid passes through the section remains constant. In this case, flow can also be defined as the product of velocity and the cross-sectional area.

>Model

ID:(875, 0)


Mechanisms
Concept


ID:(15485, 0)


Volume flow
Concept

During a time elapsed ($\Delta t$), the fluid with a mean Speed of Fluid ($v$) moves a tube element ($\Delta s$). If the section ($S$) represents the amount of fluid crossing that section in the time elapsed ($\Delta t$), it is calculated as:

$\Delta V = S \Delta s = Sv \Delta t$



This equation states that the volume of fluid flowing through section the section ($S$) during a time elapsed ($\Delta t$) is equal to the product of the cross-sectional area and the distance the fluid travels during that time.



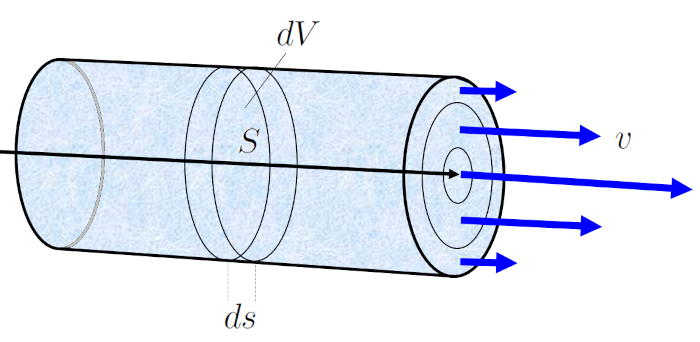
This facilitates the calculation of the volume element ($\Delta V$), which is the volume of fluid flowing through the channel in a specific period of the time elapsed ($\Delta t$), corresponding to the volume flow ($J_V$).

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

ID:(2212, 0)


Volume Flow and its Speed
Concept

Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):

$ \Delta V = S \Delta s $



Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Thus, the flow is a flux density ($j_s$), which is calculated using:

$ j_s = \displaystyle\frac{ J_V }{ S }$



It is important to note that in this model:

The flow density acts as an average velocity across the entire flow section.

ID:(15715, 0)


Variable section channel
Concept

Considering a tube that neither leaks nor receives additional liquid, the flow entering at point 1 The volume flow 1 ($J_{V1}$) will be equal to the flow exiting at point 2 The volume flow 2 ($J_{V2}$):

$ J_{V1} = J_{V2} $



Within a channel or tube, there may be a change in cross-sectional area, either widening or narrowing.



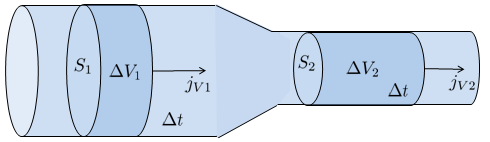
This variation will directly affect the flow through the flux density ($j_s$), which represents the velocity, increasing (if the section narrows) or decreasing (if it widens) according to the section Tube ($S$) to keep the volume flow ($J_V$) constant, as indicated by:

$ j_s = \displaystyle\frac{ J_V }{ S }$



The conservation of flow, along with the definition of flow density, leads to the conservation law such that the section in point 1 ($S_1$), the section in point 2 ($S_2$), the flux density 1 ($j_{s1}$), and the flux density 2 ($j_{s2}$) satisfy:

$ S_1 j_{s1} = S_2 j_{s2} $

ID:(2213, 0)


Validity of Continuity Equation
Concept

The continuity equation assumes that the flow is uniform, with no reverse flows or turbulence present. Therefore, it is necessary to verify that the flow is indeed laminar and free of turbulence, especially when applying the equation to analyze fluid flows in pipes and channels.There are various methods for detecting turbulence in the flow, such as using flow meters or visually observing the flow. It is essential to ensure that the flow is stable before applying the continuity equation, as any disturbance in the flow can affect the accuracy of the calculations and the overall efficiency of the system.

ID:(978, 0)


Model
Concept


ID:(15488, 0)


Flow of an incompressible liquid
Model

When a liquid is in motion, we refer to it as flow, and its measurement is based on the volume that passes through a section in a given period of time. Assuming that the volume moves without deformation, the velocity at which the liquid passes through the section remains constant. In this case, flow can also be defined as the product of velocity and the cross-sectional area.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$j_{s1}$
j_s1
Flux density 1
m/s
$j_{s2}$
j_s2
Flux density 2
m/s
$\Delta s_1$
Ds_1
Length of element 1
m
$\Delta s_2$
Ds_2
Length of element 2
m
$r_1$
r_1
Radius of Section 1
m
$r_2$
r_2
Radius of Section 2
m
$S_1$
S_1
Section in point 1
m^2
$S_2$
S_2
Section in point 2
m^2
$\Delta t$
Dt
Time elapsed
s
$J_{V1}$
J_V1
Volume flow 1
m^3/s
$J_{V2}$
J_V2
Volume flow 2
m^3/s
$\Delta V_1$
DV_1
Volume of the element 1
m^3
$\Delta V_2$
DV_2
Volume of the element 2
m^3

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):

$ \Delta V = S \Delta s $



Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Thus, the flow is a flux density ($j_s$), which is calculated using:

$ j_s = \displaystyle\frac{ J_V }{ S }$

(ID 4349)

Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):

$ \Delta V = S \Delta s $



Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Thus, the flow is a flux density ($j_s$), which is calculated using:

$ j_s = \displaystyle\frac{ J_V }{ S }$

(ID 4349)

Examples


(ID 15485)

During a time elapsed ($\Delta t$), the fluid with a mean Speed of Fluid ($v$) moves a tube element ($\Delta s$). If the section ($S$) represents the amount of fluid crossing that section in the time elapsed ($\Delta t$), it is calculated as:

$\Delta V = S \Delta s = Sv \Delta t$



This equation states that the volume of fluid flowing through section the section ($S$) during a time elapsed ($\Delta t$) is equal to the product of the cross-sectional area and the distance the fluid travels during that time.



This facilitates the calculation of the volume element ($\Delta V$), which is the volume of fluid flowing through the channel in a specific period of the time elapsed ($\Delta t$), corresponding to the volume flow ($J_V$).

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$

(ID 2212)

Flow is defined as the volume the volume element ($\Delta V$) divided by time the time elapsed ($\Delta t$), which is expressed in the following equation:

$ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$



and the volume equals the cross-sectional area the section Tube ($S$) multiplied by the distance traveled the tube element ($\Delta s$):

$ \Delta V = S \Delta s $



Since the distance traveled the tube element ($\Delta s$) per unit time the time elapsed ($\Delta t$) corresponds to the velocity, it is represented by:

$ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$



Thus, the flow is a flux density ($j_s$), which is calculated using:

$ j_s = \displaystyle\frac{ J_V }{ S }$



It is important to note that in this model:

The flow density acts as an average velocity across the entire flow section.

(ID 15715)

Considering a tube that neither leaks nor receives additional liquid, the flow entering at point 1 The volume flow 1 ($J_{V1}$) will be equal to the flow exiting at point 2 The volume flow 2 ($J_{V2}$):

$ J_{V1} = J_{V2} $



Within a channel or tube, there may be a change in cross-sectional area, either widening or narrowing.



This variation will directly affect the flow through the flux density ($j_s$), which represents the velocity, increasing (if the section narrows) or decreasing (if it widens) according to the section Tube ($S$) to keep the volume flow ($J_V$) constant, as indicated by:

$ j_s = \displaystyle\frac{ J_V }{ S }$



The conservation of flow, along with the definition of flow density, leads to the conservation law such that the section in point 1 ($S_1$), the section in point 2 ($S_2$), the flux density 1 ($j_{s1}$), and the flux density 2 ($j_{s2}$) satisfy:

$ S_1 j_{s1} = S_2 j_{s2} $

(ID 2213)

The continuity equation assumes that the flow is uniform, with no reverse flows or turbulence present. Therefore, it is necessary to verify that the flow is indeed laminar and free of turbulence, especially when applying the equation to analyze fluid flows in pipes and channels.There are various methods for detecting turbulence in the flow, such as using flow meters or visually observing the flow. It is essential to ensure that the flow is stable before applying the continuity equation, as any disturbance in the flow can affect the accuracy of the calculations and the overall efficiency of the system.

(ID 978)


(ID 15488)

ID:(875, 0)