User:
Lever Law
Model 
The lever law corresponds to a system exposed to two equal and opposite torques with which the system remains in equilibrium.
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
(ID 3241)
(ID 3241)
In the case of a balance, a gravitational force acts on each arm, generating a torque
| $ T = r F $ |
If the lengths of the arms are $d_i$ and the forces are $F_i$ with $i=1,2$, the equilibrium condition requires that the sum of the torques be zero:
| $\displaystyle\sum_i \vec{T}_i=0$ |
Therefore, considering that the sign of each torque depends on the direction in which it induces rotation,
$d_1F_1-d_2F_2=0$
which results in
| $ d_1 F_1 = d_2 F_2 $ |
.
(ID 3250)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Si se deriva en el tiempo la relaci n para el momento angular
| $ L = r p $ |
para el caso de que el radio sea constante
$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$
por lo que
| $ T = r F $ |
(ID 4431)
Examples
(ID 15845)
Since the torque generated by the gravitational force and the lever arm is
| $ T = r F $ |
on each side of the balance, it must cancel out in the case of equilibrium to achieve balance:
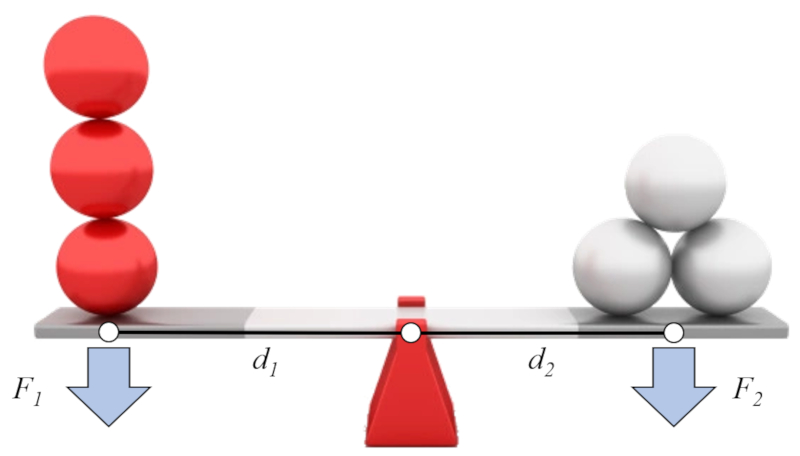
If we assume that on one side we have the force 1 ($F_1$) and the force - axis distance (arm) 1 ($d_1$), and on the other side the force 2 ($F_2$) and the force - axis distance (arm) 2 ($d_2$), we can establish the well-known lever law as follows:
| $ d_1 F_1 = d_2 F_2 $ |
(ID 15847)
(ID 15846)
ID:(1457, 0)