Flujo turbulento por tubos
Storyboard 
Si el número de Reynolds es superior a 2000, el flujo en un tubo se vuelve siempre inestable y termina siendo completamente turbulento. Con esto, ya no es posible usar la aproximación de flujo laminar viscoso que da origen a la ley de Hagen Poiseuille, y es necesario desarrollar un modelo alternativo.
El modelo que describe un flujo en el cual la viscosidad es irrelevante es el que da origen a la ecuación de Bernoulli. Sin embargo, este modelo asume que la densidad de energía se conserva. Una alternativa es asumir que las turbulencias llevan a una mezcla mediante la cual la densidad de energía no se conserva pero permanece constante. En tal caso, el flujo se puede modelar mediante una ecuación similar a la de Bernoulli, pero teniendo en cuenta una corrección debido a la homogeneización causada por la mezcla.
ID:(1970, 0)
Flujo en el límite laminar
Nota 
Si reemplazamos el factor de fricción de Darcy-Weisbach en el límite laminar, dado por
| $ f_D = \displaystyle\frac{64}{ Re }$ |
en la ecuación de Darcy-Weisbach, expresada como
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
y utilizamos la definición del número de Reynolds $Re$, podemos demostrar que el flujo está gobernado por
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
que corresponde a la ecuación de Hagen-Poiseuille.
ID:(14530, 0)
Flujo turbulento por tubos
Descripción 
Si el número de Reynolds es superior a 2000, el flujo en un tubo se vuelve siempre inestable y termina siendo completamente turbulento. Con esto, ya no es posible usar la aproximación de flujo laminar viscoso que da origen a la ley de Hagen Poiseuille, y es necesario desarrollar un modelo alternativo. El modelo que describe un flujo en el cual la viscosidad es irrelevante es el que da origen a la ecuación de Bernoulli. Sin embargo, este modelo asume que la densidad de energía se conserva. Una alternativa es asumir que las turbulencias llevan a una mezcla mediante la cual la densidad de energía no se conserva pero permanece constante. En tal caso, el flujo se puede modelar mediante una ecuación similar a la de Bernoulli, pero teniendo en cuenta una corrección debido a la homogeneización causada por la mezcla.
Variables
Cálculos
Cálculos
Ecuaciones
Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:
| $ dp = p - p_0 $ |
podemos usar la presión de la columna de agua ($p$), que es:
| $ p_t = p_0 + \rho_w g h $ |
Esto nos da:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Dado que la diferencia de altura ($\Delta h$) es:
| $ \Delta h = h_2 - h_1 $ |
la diferencia de presión ($\Delta p$) se puede expresar como:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
El flujo se define como el volumen el elemento de volumen ($\Delta V$) dividido por el tiempo el tiempo transcurrido ($\Delta t$), lo cual se expresa en la siguiente ecuaci n:
| $ J_V =\displaystyle\frac{ \Delta V }{ \Delta t }$ |
y el volumen es el producto de la secci n la sección del tubo ($S$) por el desplazamiento el elemento del tubo ($\Delta s$):
| $ \Delta V = S \Delta s $ |
Dado que el desplazamiento el elemento del tubo ($\Delta s$) dividido por el tiempo el tiempo transcurrido ($\Delta t$) equivale a la velocidad, se representa con:
| $ j_s =\displaystyle\frac{ \Delta s }{ \Delta t }$ |
Por lo tanto, el flujo es una densidad de flujo ($j_s$), que se calcula mediante:
| $ j_s = \displaystyle\frac{ J_V }{ S }$ |
(ID 4349)
La soluci n original de S.E. Haaland es la siguiente:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/R_H}{12}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Puede resolverse para obtener la expresi n del factor de fricci n $f_D$ de la siguiente manera:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{12 R_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14534)
La soluci n original de S.E. Haaland es la siguiente:
$\displaystyle\frac{1}{\sqrt{f_D}}=-1.8\log\left(\left(\displaystyle\frac{\epsilon/D_H}{3.7}\right)^{1.11} + \displaystyle\frac{6.9}{Re}\right)$
Puede resolverse para obtener la expresi n del factor de fricci n $f_D$ de la siguiente manera:
| $ f_D = \displaystyle\frac{25}{81 \log\left(\left(\displaystyle\frac{ \epsilon }{3.7 D_H }\right)^{1.11} + \displaystyle\frac{6.9}{ Re }\right)^2}$ |
(ID 14535)
La sección o superficie ($S$) del tubo que contiene el l quido se puede expresar como una funci n de la profundidad en un tubo no lleno ($h$) integrando sobre el radio hasta el radio del tubo ($R$):
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Si desarrollamos esta expresi n en t rminos del factor $h/R$ en el l mite $h\ll R$, obtenemos en primer orden:
$S = \sqrt{\displaystyle\frac{2^3}{3^2} R h ^3}$
Si resolvemos para la profundidad, obtenemos finalmente:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 14541)
Dado que el ngulo entre el radio en el borde de la superficie del l quido y la vertical se puede calcular con la profundidad en un tubo no lleno ($h$) y el radio del tubo ($R$) mediante:
$\phi =\arccos\left(1-\displaystyle\frac{h}{R}\right)$
El arco correspondiente es $R\phi$, por lo tanto, el arco total es:
$2 R \arccos\left(1-\displaystyle\frac{h}{R}\right)$
De manera an loga, la mitad de la superficie se puede determinar utilizando el teorema de Pit goras, lo que resulta en:
$\sqrt{2Rh - h^2}$
Por lo tanto, el perímetro hidrodinamico ($P_H$) se expresa como:
$P_H = 2\sqrt{2Rh - h^2}+2R\arcsin\left(1-\displaystyle\frac{h}{R}\right)$
En el l mite de una altura peque a, donde $h\ll R$, esta expresi n se puede desarrollar, resultando en:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 14542)
Ejemplos
Cuando se modela el flujo en un tubo, bajo la suposici n de que la densidad de energ a se conserva, se obtiene la ecuaci n de Bernoulli. Esta ecuaci n describe el flujo mediante la diferencia de presión ($\Delta p$) en t rminos de la densidad del líquido ($\rho_w$), la velocidad media del fluido ($v$) y la diferencia de velocidad entre superficies ($\Delta v$):
| $ \Delta p = - \rho \bar{v} \Delta v $ |
En el caso de flujo turbulento, el proceso de mezclado act a como una fricci n que reduce el gradiente de velocidad presente en el flujo laminar entre el centro y las paredes del conducto. Si asumimos que este proceso de mezclado puede ser modelado con un simple factor de correcci n, llegamos emp ricamente a la ecuaci n de Darcy-Weisbach, que involucra el factor de fricción de Darcy-Weisbach ($f_D$), el largo de tubo ($\Delta L$) y la diámetro hidrodinámico ($D_H$):
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
El factor el factor de fricción de Darcy-Weisbach ($f_D$) ha sido determinado de forma emp rica para diversas condiciones de flujo y se expresa en funci n de el número de Reynold ($Re$).
(ID 15893)
En 1944, Lewis Ferry Moody realiz mediciones del factor de fricci n de Darcy-Weisbach en funci n del n mero de Reynolds y de la rugosidad relativa de la pared, lo que result en la creaci n del siguiente diagrama:
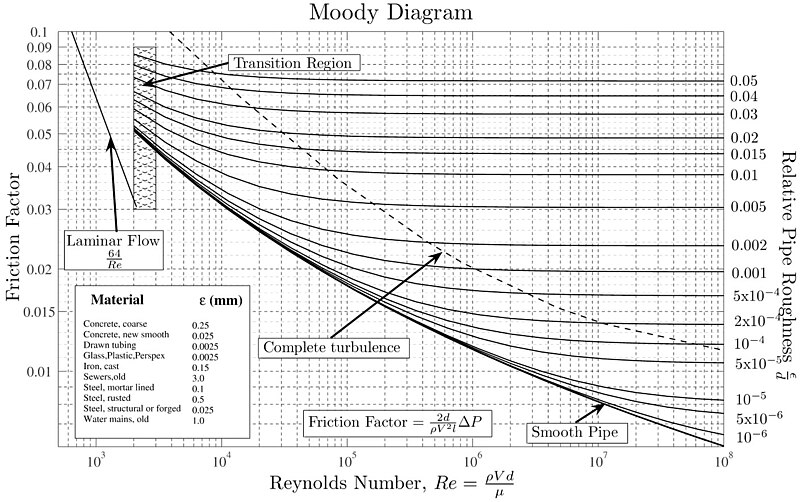
La rugosidad relativa se puede estimar considerando el tama o de las rugosidades (altura de elementos que sobresalen o profundidades de hendiduras) en relaci n con el di metro hidrodin mico.
Se observan dos comportamientos distintos:
• Para n meros de Reynolds inferiores a 2000, el factor de fricci n de Darcy-Weisbach depende solo del n mero de Reynolds, siguiendo una relaci n de $64/Re$. Esto corresponde al r gimen laminar.
• Para n meros de Reynolds superiores a 2000, se observa un comportamiento que depende tanto del n mero de Reynolds como de la rugosidad relativa de la superficie del tubo.
(ID 14528)
En el contexto de la ecuaci n de Darcy-Weisbach, se utiliza una diámetro hidrodinámico ($D_H$), que representa una generalizaci n del di metro tradicional de un c rculo. Esto permite considerar una secci n que no sea circular y calcular un di metro equivalente basado en el rea de la sección del tubo ($S$) y su el perímetro ($P$) mediante la siguiente f rmula:
| $ D_H = \displaystyle\frac{ 4 S }{ P }$ |
Para una secci n circular, recuperamos el di metro tradicional de un c rculo de la siguiente manera:
$D_H = \displaystyle\frac{4 S}{P} = \displaystyle\frac{4 \pi R^2}{2 \pi R} = 2R$
(ID 15894)
En el contexto del factor de fricci n de Darcy-Weisbach, se utiliza un radio hidráulico ($R_H$), que es una generalizaci n del radio tradicional de un c rculo. De esta forma, es posible calcular un di metro basado en el rea de la sección del tubo ($S$) y su per metro en contacto con el perímetro hidrodinamico ($P_H$), utilizando la siguiente f rmula:
| $ R_H = \displaystyle\frac{ S }{ P_H }$ |
Para una secci n circular, podemos obtener el radio hidr ulico tradicional de un c rculo de la siguiente manera:
$R_H = \displaystyle\frac{S}{P} = \displaystyle\frac{\pi R^2}{2 \pi R} = \displaystyle\frac{1}{2} R$
(ID 15895)
En un tubo cil ndrico, la profundidad est relacionada con el flujo de la siguiente manera:

Si integramos la sección o superficie ($S$), podemos calcular c mo var a la superficie en funci n de la profundidad en un tubo no lleno ($h$) mediante la integral sobre el radio hasta el radio del tubo ($R$), lo que resulta en:
$S = 2\displaystyle\int_0^h dz \sqrt{2Rz - z^2}=\displaystyle\frac{1}{2}(R-h)\sqrt{2Rh - h^2}+\displaystyle\frac{1}{2}R^2\arcsin\left(\displaystyle\frac{1-h}{R}\right)$
Para flujos peque os, donde la profundidad es significativamente menor que el radio, la relaci n entre la secci n y la profundidad se simplifica considerablemente. Al resolver la ecuaci n de profundidad, obtenemos:
| $ h = \left(\displaystyle\frac{3^2 S^2 }{2^3 R }\right)^{1/3}$ |
(ID 15896)
El perímetro hidrodinamico ($P_H$) en un tubo parcialmente lleno corresponde a los bordes de la secci n que est n en contacto con el l quido, es decir, el arco que toca la pared del tubo y la superficie:

De esta manera, podemos expresarlo en funci n de el radio del tubo ($R$) y la profundidad en un tubo no lleno ($h$) como:
$P_H = 2 R \arccos\left(1-\displaystyle\frac{h}{R}\right) + 2\sqrt{2Rh-h^2}$
Para flujos peque os, donde la profundidad es considerablemente menor que el radio, esta relaci n se simplifica y establece una conexi n m s directa entre la secci n transversal y la profundidad:
| $ P_H = \sqrt{2^5 R h }$ |
(ID 15897)
Si reemplazamos el factor de fricci n de Darcy-Weisbach en el l mite laminar, dado por
| $ f_D = \displaystyle\frac{64}{ Re }$ |
en la ecuaci n de Darcy-Weisbach, expresada como
| $ \Delta p = \displaystyle\frac{ \Delta L }{ D_H } f_D \displaystyle\frac{1}{2} \rho_w j_s ^2 $ |
y utilizamos la definici n del n mero de Reynolds $Re$, podemos demostrar que el flujo est gobernado por
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
que corresponde a la ecuaci n de Hagen-Poiseuille.
(ID 14530)
ID:(1970, 0)
