Usuario:
Comportamiento Caótico
Definición 
Lo interesante es que la ecuación de Feigenbaum muestra comportamiento caótico. Se puede definir el comportamiento caótico como la situación en que para dos valores iniciales infinitesimalmente distintos con el tiempo sus series divergen perdiéndose toda correlación entre estas. Por ello siempre se ha asumido que ecuaciones de este tipo permiten modelar el comportamiento de flujos turbulentos.
ID:(1051, 0)
Solución gráfica de la Función de Feigenbaum
Imagen
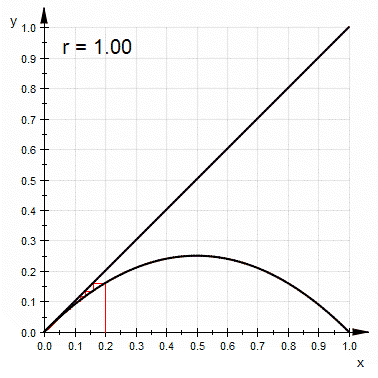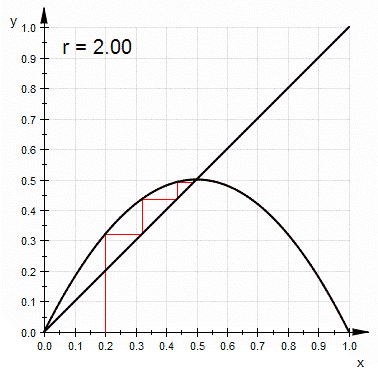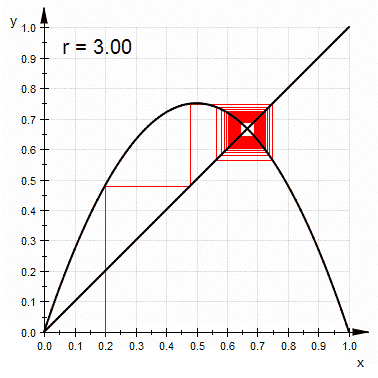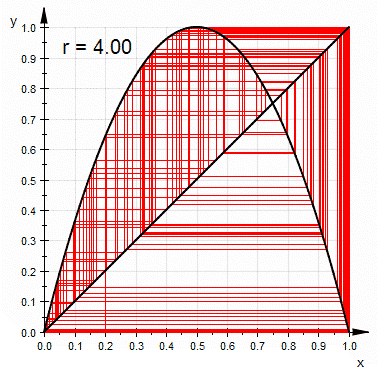
Si se dibuja en una gráfica una
- la recta $y=x_n$ y
- la parábola invertida $y=rx_n(1-x_n)$
se puede en forma alternada primero localizar el valor $y$ en la parábola, ir usando la recta al nuevo valor de $x$ que corresponde al $x_{n+1}$ y así sucesivamente:
ID:(8504, 0)
Valores asintoticos según factor $r$
Nota
Los puntos de convergencia de la ecuación de Feigenbaum (los atractores) se pueden graficar en función del parámetro $r$. De esta forma se ve que existen cuatro distintos comportamientos:
- para $r\in [0,1]$ converge siempre a cero
- para $r\in (1,2]$ converge a $(r-1)/r$
- para $r\in (2,3]$ oscila antes de converger a $(r-1)/r$
- para $r\in (3,3.44949]$ oscila entre dos puntos
- para $r\in (3.44949,3.54409]$ oscila entre cuatro valores
- para $r$ sobre 3.54409 va oscila entre 8, 16, 32, etc. según el valor $r$ y mientras sea este menor que y 3.56995
- para $r$ mayor que 3.56995 el comportamiento se vuelve caótico.
El la siguiente gráfica se muestran los valores asintomáticos para valores de $r$ superiores a 2.4:
ID:(8503, 0)
Series para distintos $r$
Cita
Si se grafican las series para distintos valores de $r$ se obtienen los siguientes diagramas:
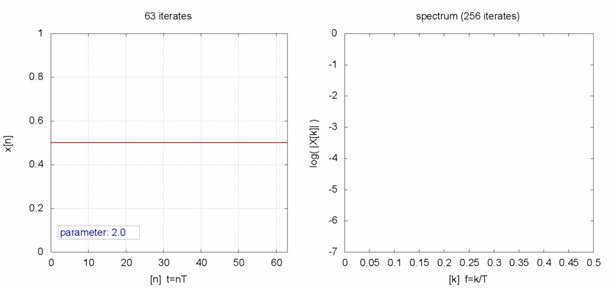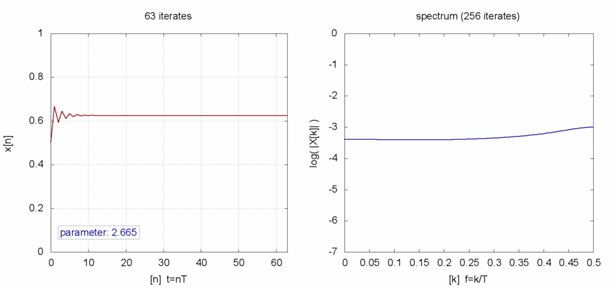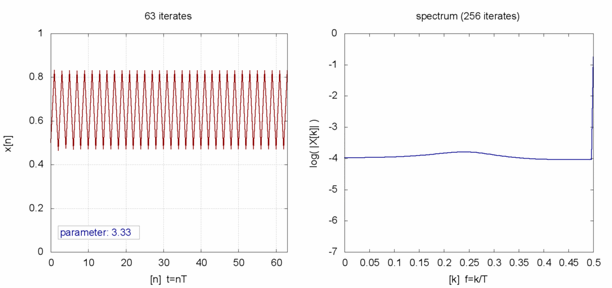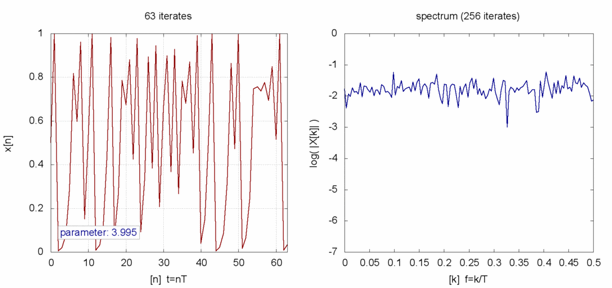
ID:(2345, 0)
Primer Programa
Descripción
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Michael feigenbaum en los a os 70 comenz a jugar (literalmente) con ecuaciones de iteraci n no lineales, en particular con ecuaciones que simulaban comportamientos tipo desarrollo de poblaciones:
- un termino lineal para lo que era fertilidad, y
- un termino cuadr tico que representa la mortalidad (cuando ocurre por interacci n - ejemplo caza)
El modelo de Feigenbaum trabaja con la ecuaci n recursiva:
$x_{n+1}=rx_n(1-x_n)$
en donde $r$ es una constante que toma valores entre 0 y 4 y $n$ es el indice que va enumerando la serie $x_n$. La serie depende de la constante $r$ y del valor inicial que se asume para $n=0$ y se denota correspondientemente $x_0$.
(ID 4388)
Lo interesante es que la ecuaci n de Feigenbaum muestra comportamiento ca tico. Se puede definir el comportamiento ca tico como la situaci n en que para dos valores iniciales infinitesimalmente distintos con el tiempo sus series divergen perdi ndose toda correlaci n entre estas. Por ello siempre se ha asumido que ecuaciones de este tipo permiten modelar el comportamiento de flujos turbulentos.
(ID 1051)
Si se dibuja en una gr fica una
- la recta $y=x_n$ y
- la par bola invertida $y=rx_n(1-x_n)$
se puede en forma alternada primero localizar el valor $y$ en la par bola, ir usando la recta al nuevo valor de $x$ que corresponde al $x_{n+1}$ y as sucesivamente:
(ID 8504)
Los puntos de convergencia de la ecuaci n de Feigenbaum (los atractores) se pueden graficar en funci n del par metro $r$. De esta forma se ve que existen cuatro distintos comportamientos:
- para $r\in [0,1]$ converge siempre a cero
- para $r\in (1,2]$ converge a $(r-1)/r$
- para $r\in (2,3]$ oscila antes de converger a $(r-1)/r$
- para $r\in (3,3.44949]$ oscila entre dos puntos
- para $r\in (3.44949,3.54409]$ oscila entre cuatro valores
- para $r$ sobre 3.54409 va oscila entre 8, 16, 32, etc. seg n el valor $r$ y mientras sea este menor que y 3.56995
- para $r$ mayor que 3.56995 el comportamiento se vuelve ca tico.
El la siguiente gr fica se muestran los valores asintom ticos para valores de $r$ superiores a 2.4:
(ID 8503)
Si se grafican las series para distintos valores de $r$ se obtienen los siguientes diagramas:
(ID 2345)
ID:(86, 0)