(ID 15439)

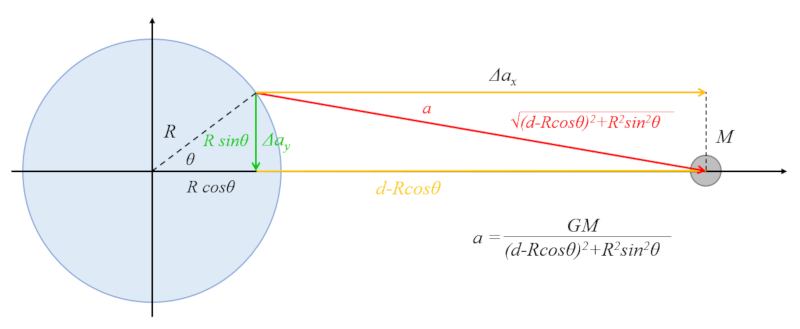
La atracci n gravitatoria de un cuerpo celeste provoca el fen meno de la marea, desplazando el agua hacia la regi n ecuatorial. Esto se ilustra en el siguiente diagrama:

En el tri ngulo mostrado, la hipotenusa se relaciona con el cateto vertical por la expresi n:

$R\sin\theta$

y con el cateto horizontal por:

$d - R\cos\theta$

De acuerdo con el teorema de Pit goras, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, por lo que obtenemos:

$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$

(ID 11635)

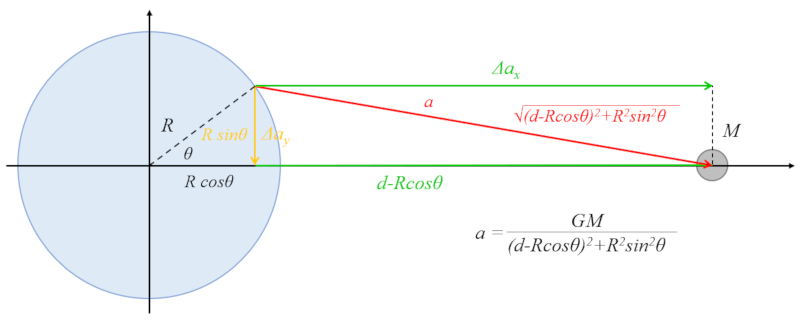
Existe uma contribui o da atra o do corpo celeste que direciona a gua em dire o ao raio, o que tende a deslocar a gua em dire o zona do equador:

A hipotenusa do tri ngulo dada pelo cateto vertical:

$R\sin\theta$

e pelo cateto horizontal:

$d - R\cos\theta$

De acordo com o teorema de Pit goras, temos:

$R^2\sin^2\theta+(d-R\cos\theta)^2=d^2+R^2-2Rd\cos\theta$

(ID 11658)

(ID 15434)

Para determinar la variaci n de la aceleraci n perpendicular al radio, podemos utilizar la similitud de tri ngulos para igualar la relaci n

$\displaystyle\frac{\Delta a_{cy}}{a_c}$

con el comprimento

$d-R\cos\theta$

y la hipotenusa

$\sqrt{d^2+R^2-2dR\cos\theta}$

.

Por la similitud de tri ngulos, tenemos con que

.

(ID 11643)

Con la ley de la gravitaci n de Newton con es:

Se puede, con la definici n de la fuerza con :

Y el radio al cuadrado:

$r^2=d^2+R^2-2dR\cos\theta$

Calcular la aceleraci n reemplazando el radio en la fuerza y despejando la aceleraci n. Lo que da con la aceleraci n:

(ID 11644)

Con , la relaci n entre la variaci n de la aceleraci n y la aceleraci n es:



Y dado que la expresi n para la aceleraci n es con :



Se sigue que:

$\Delta a_{cy} = GM\displaystyle\frac{R\sin\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\displaystyle\frac{R\sin\theta}{d}$

Por lo tanto, en la aproximaci n d\gg R, podemos aproximar con por:

(ID 11645)

Para determinar a varia o da acelera o paralela ao raio, podemos utilizar a semelhan a de tri ngulos para igualar a rela o

$\displaystyle\frac{\Delta a_{cx}}{a_c}$

com o comprimento

$d+R\cos\theta$

e a hipotenusa

$\sqrt{d^2+R^2-2dR\cos\theta}$

Por semelhan a de tri ngulos, temos com que

(ID 11647)

Con aceleración generada por el cuerpo celeste, en conjunción $m/s^2$, distancia planeta objeto celeste $m$, latitud del lugar $rad$, radio del planeta $m$ y variación de aceleración en dirección del astro, en conjunción $m/s^2$, la relaci n es:

Y como para aceleración generada por el cuerpo celeste, en conjunción $m/s^2$, constante Universal de Gravitación $m^3/kg s^2$, distancia planeta objeto celeste $m$, latitud del lugar $rad$, masa del cuerpo que genera la marea $kg$ y radio del planeta $m$,

Entonces, se sigue que:

$\Delta a_{cx} =GM\displaystyle\frac{d - R\cos\theta}{(d^2 + R^2 - 2dR\cos\theta)^{3/2}}\sim \displaystyle\frac{GM}{d^2}\left(1+\displaystyle\frac{2R\cos\theta}{d}\right)$

Por lo tanto, en la aproximaci n d\gg R, podemos aproximar con por:

(ID 11650)