Storyboard

La convección transporta masas de aire y evaporación de agua generado en la superficie, lleva energía de la superficie a la atmósfera.

Las precipitaciones lleva energía de la atmósfera a la superficie.

Ambos procesos afectan el balance energético y con ello el clima.

>Modelo

ID:(1215, 0)

Definición

Si observamos la distribución del calor transportado por calor latente en la superficie del planeta, se puede notar que depende de la humedad relativa. Por lo tanto, alcanza valores cercanos a $150 W/m^2$ sobre los océanos en zonas ecuatoriales, disminuyendo a $30 W/m^2$ en zonas continentales y llegando a cero en áreas desérticas:

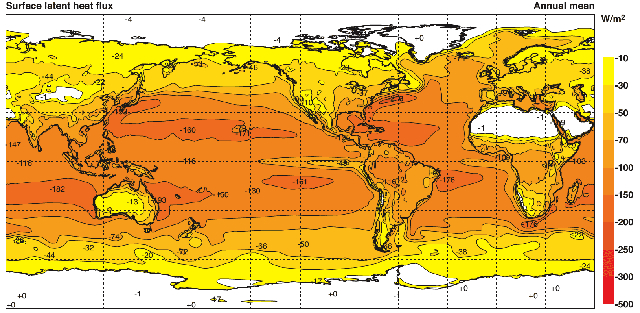
Promedio anual de calor transportado por calor latente calculado de ECMWF 40-años reanalizados (Kallberg et al 2005). Cuidado: este diagrama usa la convención de que un flujo ascendente es negativo a diferencia que el presente texto que la define como positiva.

Estos datos provienen del reanálisis de 40 años realizado por Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Reino Unido, Proyecto de Reanálisis de ECMWF (Kallberg et al 2005).

ID:(9264, 0)

Imagen

ID:(3076, 0)

Nota

Uno de los mecanismos clave en el proceso de flujo de energía en el sistema climático es la evaporación. En este proceso, el agua se evapora en un lugar, extrayendo energía de la superficie, y luego se transporta por convección hasta la atmósfera, donde libera nuevamente la energía mediante la condensación.

Ciclo del agua que indica los distintos flujos y los principales volúmenes de agua anuales.

La energía que fluye anualmente a través del transporte de calor latente es igual al flujo de $I_E\sim 80,W/m^2$ multiplicado por la superficie del planeta, con un radio $R\sim 6.37\times 10^{+6}m$ y el número de segundos en un año $t_e=3.15\times 10^{+7}s$.

$Q_e=4\pi R^2 I_E t_e=1.27\times 10^{24},J$

Si el calor latente es igual a $L_v=2256,kJ/kg$ y la densidad del agua es $\rho_w=1000,kg/m^3$, se obtiene el volumen de agua evaporada por año:

$V_w=\displaystyle\frac{Q_e}{\rho_wL_v}=5\times 10^{14}m^3$

De este volumen de agua, el 87% se evapora sobre los océanos, mientras que el resto proviene de zonas húmedas continentales. El agua regresa a la superficie a través de la lluvia o la nieve. Del total, el 77% corresponde a la lluvia sobre los océanos, lo cual es ligeramente superior a la proporción de superficie ocupada por los océanos.

ID:(9266, 0)

Cita

ID:(9268, 0)