(ID 15667)


earth009

(ID 3074)

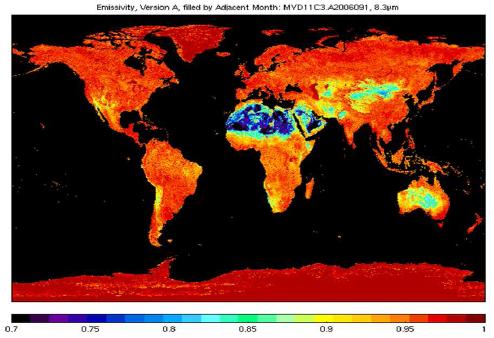
La emisividad de la superficie fluctuar entre 0.7 (oc ano), 0.8 (desiertos), 0.9 (nieve) y 1.0 (vegetaci n):

(ID 3073)


earth011

(ID 3075)

Wie bei der sichtbaren Strahlung interagiert die Atmosph re auch mit der Infrarotstrahlung. hnlich wie die Interaktion mit der Atmosph re im Fall der sichtbaren Strahlung unter Verwendung von die Sichtbare Abdeckung (VIS) ($\gamma_v$) modelliert wird, kann man ERROR:7452 einf hren, das die Infrarotstrahlung beeinflusst.

Daher ist die NIR-Intensität, die von der Erde in den Weltraum emittiert wird ($I_{es}$) gleich die Von der Erde emittierte NIR-Intensität ($I_e$), gewichtet durch einen Faktor, der von ERROR:7452 abh ngt, sodass:

(ID 4677)

Von der terrestrischen Strahlung $I_e$, die gr tenteils

Der Anteil der Strahlung, der mit der Atmosph re interagiert, wird mithilfe der Abdeckung $\gamma$ berechnet, gem

(ID 4684)

Wenn die Erde eine Temperatur von $T_e$ hat, strahlt sie gem dem Stefan-Boltzmann-Gesetz mit einer Intensit t, die durch die folgende Formel gegeben ist:



Dabei ist $\sigma$ die Stefan-Boltzmann-Konstante und $\epsilon$ der Emissionskoeffizient. Die Stefan-Boltzmann-Konstante $\sigma$ hat einen Wert von ungef hr $5.67 \times 10^{-8} W/m^2K^4$, und der Emissionskoeffizient $\epsilon$ repr sentiert die Effizienz, mit der die Oberfl che der Erde Strahlung emittiert und liegt zwischen 0 und 1.

(ID 4676)

Die Intensit t $I$, die von einem K rper bei einer Temperatur $T$ abgegeben wird, wird durch das Stefan-Boltzmann-Gesetz geregelt. Es lautet:

wobei $\epsilon$ die Emissionsf higkeit und $\sigma$ die Stefan-Boltzmann-Konstante ist. Daher wird im Fall des unteren Rands der Wolke, der eine Temperatur $T_b$ aufweist, die Intensit t sein:

(ID 4679)

Si la parte superior de la atm sfera esta a una temperatura T_t, emite radiaci n, en su mayor a con

que en este caso resulta con

donde \sigma es la constante de Stefan Boltzmann y \epsilon el coeficiente de emisividad.

(ID 4680)

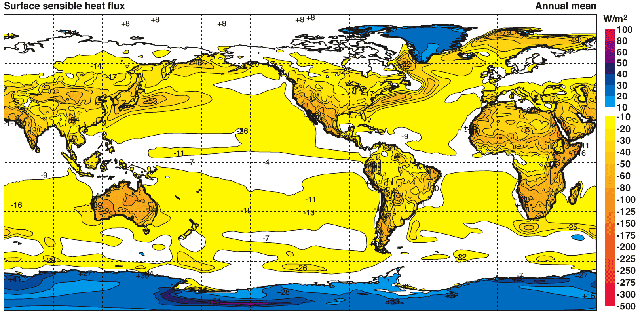
Wenn wir die Verteilung der durch Konvektion transportierten W rme ber die Oberfl che des Planeten betrachten, f llt auf, dass es mehr oder weniger konstante Ebenen gibt. Auf der einen Seite haben wir ozeanische und kontinentale Gebiete mit einem Fluss von etwa $17 W/m^2$ (aufw rts) und ungef hr $-30 W/m^2$ (abw rts) in Bereichen, die mit Schnee und Eis bedeckt sind:

None

Diese Daten stammen aus einer 40-j hrigen Reanalyse von Kallberg P., Berrisford P., Hoskins B., Simmons A., Uppala S., Lamy-Thepaut S., Hine R., 2005: ERA-40 Atlas. Reading, Vereinigtes K nigreich, ECMWF Re-Analysis Project (Kallberg et al., 2005).

(ID 9263)

Si se observa la radiaci n de onda larga (NIR) se ve que existe un m ximo en torno al mes de agosto/septiembre de todos los a os:



Esto se debe a que el hemisferio norte presenta mayor masas continentales por lo que estas reflejan mayormente cuando es verano en dicho hemisferio..

(ID 9324)

La radiaci n de onda larga (NIR) es en primera aproximaci n sim trica en torno al ecuador fuera de presentar un m ximo en torno de los grados -20 y +20:



Esto corresponde tanto a la falta de masa continental en torno al ecuador y la baja de intensidad hacia los polos por efecto de la incidencia inclinada de la radiaci n.

(ID 9325)

Durch die Modellierung von die Durch Leitung und Verdunstung übertragene Energie ($I_d$) kann eine Beziehung f r den W rmetransport etabliert werden, die die Differenz zwischen ERROR:6516 und die Temperature der Unterseite der Atmosphäre emittiert ($T_b$) sowie ERROR:8094 einschlie t, was im Prozess entscheidend ist. Die Gleichung umfasst zwei Konstanten, ERROR:8093 und ERROR:6521, so dass:

ERROR:8093 liegt in der Gr enordnung von 10,0 W/m , und ERROR:6521 in der Gr enordnung von 0,16 W/m K, wobei ERROR:8094 typischerweise etwa 8 m/s betr gt.

ERROR:8093 stammt haupts chlich aus der Energie, die durch die Bewegung von feuchten Luftmassen transportiert wird, die bei der Kondensation Energie freisetzen. ERROR:6521 resultiert aus dem Lufttransport durch Konvektion und die entsprechende adiabatische Expansion, sodass es haupts chlich vom Temperaturgradienten abh ngt.

(ID 15682)

(ID 15678)

Die Abgestrahlte Intensität ($I_i$) ist der Anteil, der durch ERROR:8393 von ERROR:8390 definiert wird und wie folgt berechnet wird:

(ID 9986)

Die Abgestrahlte Intensität ($I_t$) ist gleich ERROR:8390 abz glich ERROR:8393, so dass es lautet:

(ID 10324)

Das Stefan-Boltzmann-Gesetz besagt, dass die Abgestrahlte Intensität ($I$) eine Funktion von die Temperatur ($T$) ist, unter Verwendung der Konstanten die Emissionsgrad ($\epsilon$) und die Stefan Boltzmann Konstante ($\sigma$), wie folgt:

(ID 14479)

Das Stefan-Boltzmann-Gesetz besagt, dass die Abgestrahlte Intensität ($I$) eine Funktion von die Temperatur ($T$) ist, unter Verwendung der Konstanten die Emissionsgrad ($\epsilon$) und die Stefan Boltzmann Konstante ($\sigma$), wie folgt:

(ID 14479)

Das Stefan-Boltzmann-Gesetz besagt, dass die Abgestrahlte Intensität ($I$) eine Funktion von die Temperatur ($T$) ist, unter Verwendung der Konstanten die Emissionsgrad ($\epsilon$) und die Stefan Boltzmann Konstante ($\sigma$), wie folgt:

(ID 14479)

Die Durch Leitung und Verdunstung übertragene Energie ($I_d$) h ngt von der Differenz zwischen die Temperature der Unterseite der Atmosphäre emittiert ($T_b$) und ERROR:6516 sowie von ERROR:8094 und den Konstanten ERROR:8093 und ERROR:6521 folgenderma en ab:

(ID 9270)