Schwingungen von Wassermolekülen
Definition 
Wassermoleküle sind in der Lage, in verschiedenen Modi zu schwingen.
Immer wenn eine Lichtwelle mit einer Frequenz auftritt, die mit der Schwingungsfrequenz des Modus übereinstimmt, passieren zwei Dinge:
• Der Modus des Moleküls wird aktiviert.
• Die für die Aktivierung des Modus erforderliche Energie wird von der Lichtwelle aufgenommen, wodurch ihre Intensität reduziert wird.
Mit anderen Worten, wenn eine Lichtwelle mit der Schwingungsfrequenz eines Wassermoleküls übereinstimmt, absorbiert das Molekül Energie aus dem Licht und tritt in einen spezifischen Schwingungszustand ein. Dieses Phänomen ist bei verschiedenen Prozessen wichtig, die mit der Wechselwirkung von Licht und Wasser zusammenhängen, wie beispielsweise Lichtabsorption im sichtbaren Spektrum und Lichtstreuung in optischen Phänomenen wie Regenbögen.

ID:(12467, 0)
Spektrum des Sonnenlichts
Bild 
Wenn ein Teil des Lichts, das die Erde erreicht, absorbiert wird, werden Abnahmen in der Intensität des Spektrums beobachtet:
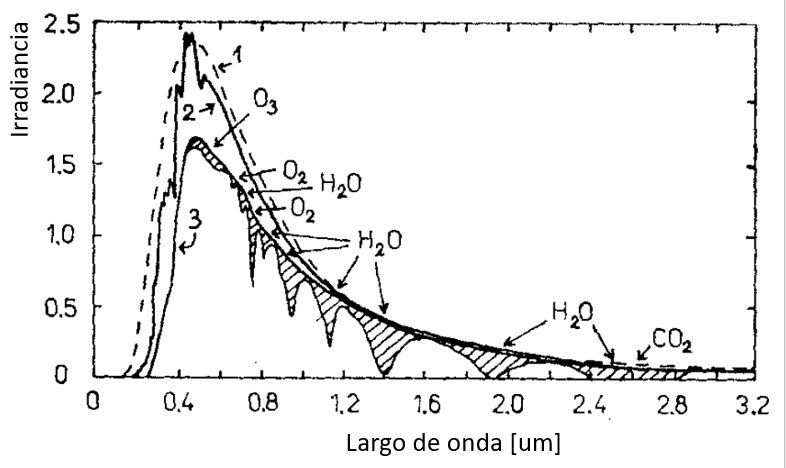
Wenn ein Teil des auf die Erde treffenden Lichts absorbiert wird, kommt es zu einer Verringerung der Intensität des beobachteten Lichtspektrums. Dies geschieht, weil bestimmte Bestandteile des Lichts, wie bestimmte Wellenlängen, von Materialien in der Atmosphäre oder auf der Erdoberfläche absorbiert werden. Dadurch können in verschiedenen Teilen des elektromagnetischen Spektrums Abnahmen der Lichtintensität beobachtet werden.
Dieses Phänomen der Lichtabsorption ist in verschiedenen Bereichen wichtig, wie der atmosphärischen Physik, der Fotografie, der Biologie und der Chemie. Die selektive Absorption bestimmter Wellenlängen kann das Klima, die photosynthetischen Prozesse von Pflanzen und die Identifizierung chemischer Substanzen durch Spektroskopie beeinflussen.
Es ist wichtig zu beachten, dass die Abnahmen der Lichtintensität im Spektrum wertvolle Informationen über die Zusammensetzung der Atmosphäre und der Erdoberfläche liefern können, was eine bessere Erforschung und ein besseres Verständnis der physikalischen und chemischen Prozesse ermöglicht, die in unserer Umwelt stattfinden.
ID:(12468, 0)
Auswirkung von Turbulenzen in der Atmosphäre
Notiz 
Wenn es Turbulenzen in der Atmosphäre gibt, variiert die Menge an Wolken, was wiederum die Anzahl der Wassermoleküle und deren Lichtabsorption beeinflusst. Da dies nicht von der Frequenz abhängt, wird nur die Intensität des Strahls verändert, nicht aber seine Frequenz. Daher kann es zu einer Situation wie der auf dem Bild gezeigten kommen:
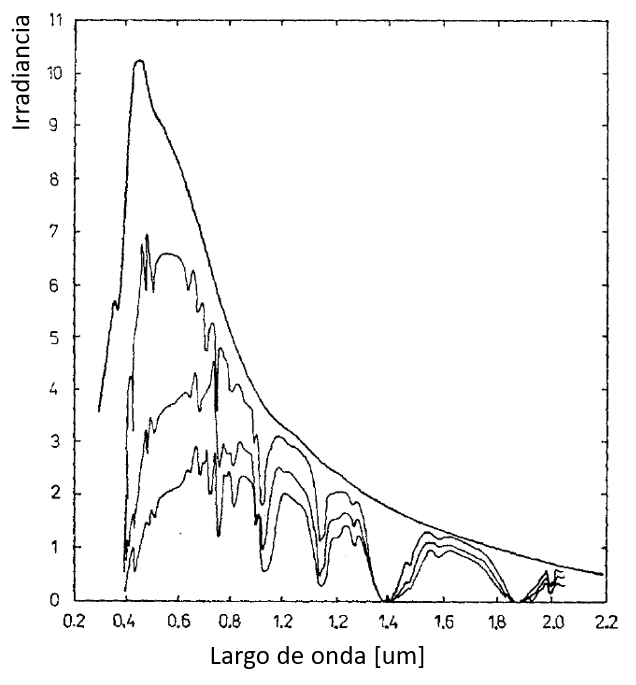
Bei atmosphärischen Turbulenzen kommt es zu einer Beeinflussung der Lichtausbreitung, was zu Schwankungen in der Anzahl der Wolken und damit auch der Anzahl der Wassermoleküle in der Atmosphäre führt. Dies kann zu einer stärkeren oder schwächeren Absorption des Lichts in verschiedenen Bereichen des elektromagnetischen Spektrums führen. Das Bild verdeutlicht, wie die Intensität des Lichts aufgrund atmosphärischer Turbulenzen schwanken kann und dadurch Unterschiede im Erscheinungsbild und der Helligkeit des Lichtstrahls entstehen.
Es ist wichtig zu beachten, dass atmosphärische Turbulenzen und ihre Auswirkungen auf die Lichtausbreitung erhebliche Auswirkungen auf die Qualität astronomischer Beobachtungen, Fotografie und andere Bereiche haben können, die auf eine stabile und gleichmäßige Beleuchtung angewiesen sind.
ID:(12469, 0)
Strahlungsfluss pro Winkelelement
Zitat 
Wenn der Strahlungsfluss von der Richtung abhängt, ergibt es Sinn, seinen Beitrag in einem definierten Winkelbereich zu berechnen. Daher ist es notwendig, das Konzept eines Winkellements einzuführen, das bei Einbeziehung aller Richtungen zu $4\pi$ führen sollte, was dem Raumwinkel einer Kugel entspricht. Es wird in der Regel als $d\Omega$ bezeichnet und entspricht einer Art Kegel, wie im folgenden Diagramm dargestellt:
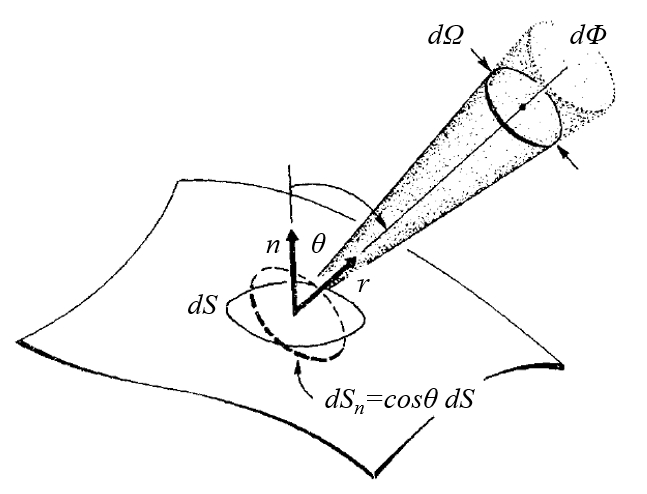
Dieses Diagramm veranschaulicht, wie das Winkellement $d\Omega$ definiert ist. Es repräsentiert einen Bereich im Raum, der einen infinitesimalen Kegel mit seinem Scheitelpunkt am Interessenspunkt umfasst. Die Größe des Winkellements $d\Omega$ hängt von der Größe des Kegels ab und kann je nach Geometrie des Systems variieren.
ID:(12476, 0)
Winkelelement
Übung 
In grafischer Form wird das Winkel-Element in Koordinaten durch einen Bogen des Azimutwinkels und einen weiteren Bogen des Polarwinkels multipliziert mit dem Sinus des letzteren gebildet.
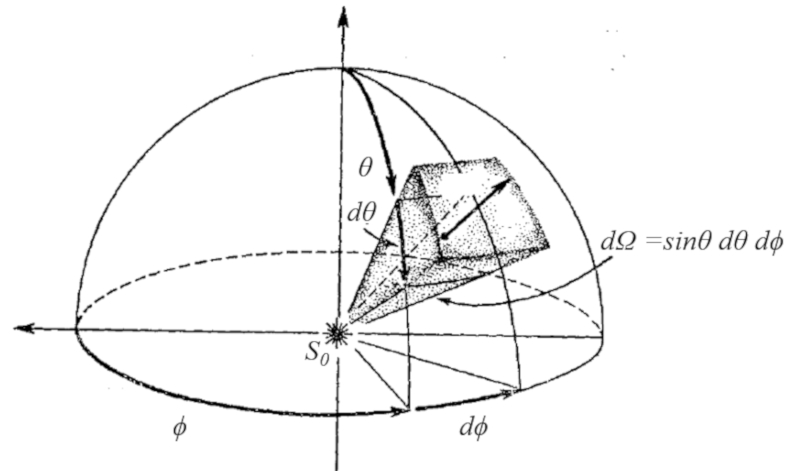
Die grafische Darstellung eines Winkel-Elements in Koordinaten ist entscheidend, um zu visualisieren und zu verstehen, wie es sich im Raum erstreckt. Dabei wird ein Bogen in der horizontalen Ebene gezeichnet, der dem Azimutwinkel entspricht, und ein weiterer Bogen in der vertikalen Ebene, der dem Polarwinkel entspricht. Die Größe des Bogens des Polarwinkels wird mit dem Sinus dieses Winkels multipliziert, um die Projektion in der horizontalen Ebene zu berücksichtigen.
ID:(12475, 0)
Coeficiente de absorción en el infrarrojo (NIR)
Gleichung 
Los valores del coeficiente de absorción son mayores en el rango infrarrojo debido en parte a lo que se denomina la sustancia amarilla que corresponde a los restos de vida orgánica. El coeficiente se va reduciendo en dirección de largos de onda mayores que corresponden a el rango visible (VIS):
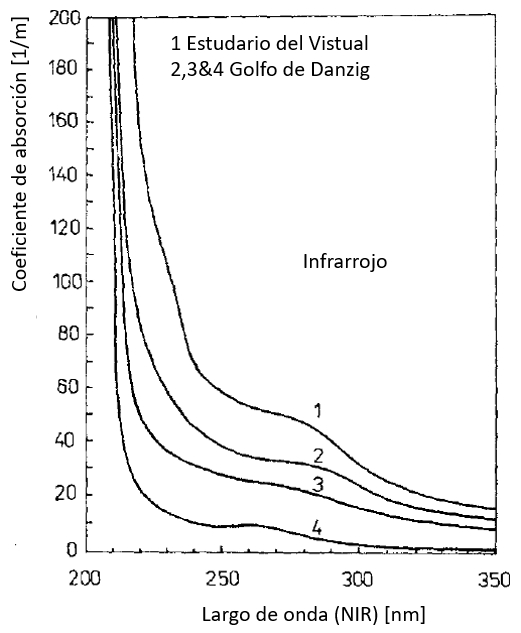
ID:(12478, 0)
Coeficiente de absorción en el rango visible (VIS)
Script 
Los valores del coeficiente de absorción en el rango visible (VIS) pasan por un mínimo creciendo para largos de onda mayores:
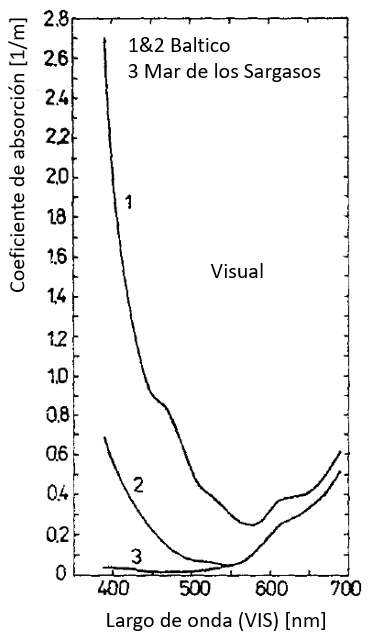
ID:(12479, 0)
Disminución del coeficiente de absorción con la profundidad
Variable 
Si se compara el coeficiente de absorción a distintas profundidades (o sea distintas presiones) se nota que en general se mantiene la forma pero se va reduciendo con la profundidad:

ID:(12480, 0)
Origen del coeficiente de absorción en función de el largo de onda
Audio 
Si se analiza el origen del coeficiente de absorción en el rango visible que ve que:
• en los largos de onda menores el efecto de la sustancia amarilla (restos de vida orgánica) domina
• otros materiales en suspensión también tiene una contribución para largos de ondas menores
• el incremento para largo de ondas mayores es propio del agua
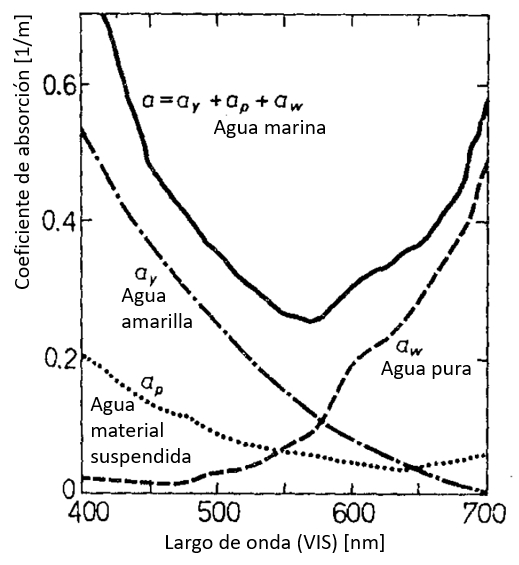
ID:(12481, 0)
Lichtabsorption
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
A medida que el haz avanza por el medio en una distancia
$\displaystyle\frac{dL}{L}$
\\n\\nes proprocional al camino recorrido
$\displaystyle\frac{dL}{L}\propto dr$
\\n\\nSi se introduce la constante de proporcionalidad como
$\displaystyle\frac{dL}{L}=-\alpha dr$
donde el signo negativo se debe a que la luminosidad se va reduciendo. Por ello la ecuaci n que rige la luminosidad es una ecuaci n de primer orden
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
(ID 12470)
La integraci n de la ecuaci n diferencial
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
\\n\\npara una luminosidad
$\displaystyle\int_0^{L_0} \displaystyle\frac{dL}{L} = -\displaystyle\int_0^{r}\alpha dr$
lo que arroja
| $ L = L_0 e^{- \alpha r } $ |
(ID 12477)
Beispiele
Wassermolek le sind in der Lage, in verschiedenen Modi zu schwingen.
Immer wenn eine Lichtwelle mit einer Frequenz auftritt, die mit der Schwingungsfrequenz des Modus bereinstimmt, passieren zwei Dinge:
• Der Modus des Molek ls wird aktiviert.
• Die f r die Aktivierung des Modus erforderliche Energie wird von der Lichtwelle aufgenommen, wodurch ihre Intensit t reduziert wird.
Mit anderen Worten, wenn eine Lichtwelle mit der Schwingungsfrequenz eines Wassermolek ls bereinstimmt, absorbiert das Molek l Energie aus dem Licht und tritt in einen spezifischen Schwingungszustand ein. Dieses Ph nomen ist bei verschiedenen Prozessen wichtig, die mit der Wechselwirkung von Licht und Wasser zusammenh ngen, wie beispielsweise Lichtabsorption im sichtbaren Spektrum und Lichtstreuung in optischen Ph nomenen wie Regenb gen.

(ID 12467)
Wenn ein Teil des Lichts, das die Erde erreicht, absorbiert wird, werden Abnahmen in der Intensit t des Spektrums beobachtet:

Wenn ein Teil des auf die Erde treffenden Lichts absorbiert wird, kommt es zu einer Verringerung der Intensit t des beobachteten Lichtspektrums. Dies geschieht, weil bestimmte Bestandteile des Lichts, wie bestimmte Wellenl ngen, von Materialien in der Atmosph re oder auf der Erdoberfl che absorbiert werden. Dadurch k nnen in verschiedenen Teilen des elektromagnetischen Spektrums Abnahmen der Lichtintensit t beobachtet werden.
Dieses Ph nomen der Lichtabsorption ist in verschiedenen Bereichen wichtig, wie der atmosph rischen Physik, der Fotografie, der Biologie und der Chemie. Die selektive Absorption bestimmter Wellenl ngen kann das Klima, die photosynthetischen Prozesse von Pflanzen und die Identifizierung chemischer Substanzen durch Spektroskopie beeinflussen.
Es ist wichtig zu beachten, dass die Abnahmen der Lichtintensit t im Spektrum wertvolle Informationen ber die Zusammensetzung der Atmosph re und der Erdoberfl che liefern k nnen, was eine bessere Erforschung und ein besseres Verst ndnis der physikalischen und chemischen Prozesse erm glicht, die in unserer Umwelt stattfinden.
(ID 12468)
Wenn es Turbulenzen in der Atmosph re gibt, variiert die Menge an Wolken, was wiederum die Anzahl der Wassermolek le und deren Lichtabsorption beeinflusst. Da dies nicht von der Frequenz abh ngt, wird nur die Intensit t des Strahls ver ndert, nicht aber seine Frequenz. Daher kann es zu einer Situation wie der auf dem Bild gezeigten kommen:

Bei atmosph rischen Turbulenzen kommt es zu einer Beeinflussung der Lichtausbreitung, was zu Schwankungen in der Anzahl der Wolken und damit auch der Anzahl der Wassermolek le in der Atmosph re f hrt. Dies kann zu einer st rkeren oder schw cheren Absorption des Lichts in verschiedenen Bereichen des elektromagnetischen Spektrums f hren. Das Bild verdeutlicht, wie die Intensit t des Lichts aufgrund atmosph rischer Turbulenzen schwanken kann und dadurch Unterschiede im Erscheinungsbild und der Helligkeit des Lichtstrahls entstehen.
Es ist wichtig zu beachten, dass atmosph rische Turbulenzen und ihre Auswirkungen auf die Lichtausbreitung erhebliche Auswirkungen auf die Qualit t astronomischer Beobachtungen, Fotografie und andere Bereiche haben k nnen, die auf eine stabile und gleichm ige Beleuchtung angewiesen sind.
(ID 12469)
Um den Strahlungsfluss zu modellieren, kann man damit beginnen, die radiative Energie pro Zeiteinheit zu beschreiben. Daher wird er wie folgt definiert:
| $ \Phi = \displaystyle\frac{d Q_e }{d t }$ |
Der Strahlungsfluss ist die Menge an radiativer Energie, die pro Zeiteinheit eine Fl che durchquert. Er wird in der Regel in Watt pro Quadratmeter (W/m ) angegeben. Diese Messgr e ist fundamental, um den Transfer von radiativer Energie in verschiedenen Ph nomenen wie solarem Aufheizen, W rmestrahlung und der Ausbreitung elektromagnetischer Wellen zu verstehen und zu studieren.
(ID 12471)
Wenn der Strahlungsfluss von der Richtung abh ngt, ergibt es Sinn, seinen Beitrag in einem definierten Winkelbereich zu berechnen. Daher ist es notwendig, das Konzept eines Winkellements einzuf hren, das bei Einbeziehung aller Richtungen zu $4\pi$ f hren sollte, was dem Raumwinkel einer Kugel entspricht. Es wird in der Regel als $d\Omega$ bezeichnet und entspricht einer Art Kegel, wie im folgenden Diagramm dargestellt:

Dieses Diagramm veranschaulicht, wie das Winkellement $d\Omega$ definiert ist. Es repr sentiert einen Bereich im Raum, der einen infinitesimalen Kegel mit seinem Scheitelpunkt am Interessenspunkt umfasst. Die Gr e des Winkellements $d\Omega$ h ngt von der Gr e des Kegels ab und kann je nach Geometrie des Systems variieren.
(ID 12476)
Wenn der Bruchteil des strahlenden Flusses, der in einem Winkelbereich bestrahlt wird, bestimmt wird, kann die Winkelverteilung des strahlenden Flusses mit folgendem Ausdruck definiert werden:
| $ \Phi = \displaystyle\frac{d Q_e }{d t }$ |
Diese Gleichung repr sentiert den Anteil des strahlenden Flusses, der durch das Winkellement im Verh ltnis zum Gesamtfluss hindurchtritt. Die Winkelverteilung des strahlenden Flusses wird erhalten, indem dieser Anteil durch das differentielle Winkellement $d\Omega$ dividiert wird.
| $ I = \displaystyle\frac{ d\Phi }{ d\Omega }$ |
Die Winkelverteilung des strahlenden Flusses liefert Informationen ber die r umliche und richtungsabh ngige Verteilung der Strahlung in einem System. Es ist eine wichtige Messgr e, um zu verstehen, wie sich strahlende Energie in verschiedenen Richtungen ausbreitet und verteilt.
(ID 12472)
In grafischer Form wird das Winkel-Element in Koordinaten durch einen Bogen des Azimutwinkels und einen weiteren Bogen des Polarwinkels multipliziert mit dem Sinus des letzteren gebildet.

Die grafische Darstellung eines Winkel-Elements in Koordinaten ist entscheidend, um zu visualisieren und zu verstehen, wie es sich im Raum erstreckt. Dabei wird ein Bogen in der horizontalen Ebene gezeichnet, der dem Azimutwinkel entspricht, und ein weiterer Bogen in der vertikalen Ebene, der dem Polarwinkel entspricht. Die Gr e des Bogens des Polarwinkels wird mit dem Sinus dieses Winkels multipliziert, um die Projektion in der horizontalen Ebene zu ber cksichtigen.
(ID 12475)
Wenn man in sph rischen Koordinaten arbeitet, kann das Winkelelement basierend auf einem Segment des Polarwinkels $\phi$ und des Azimutwinkels $\theta$ berechnet werden. Das Element des Raumwinkels wird durch diese grafische Konstruktion ermittelt.
| $ d\Omega = sin\theta d\theta d\phi$ |
(ID 12474)
Con la densidad angular del flujo radiante, definida con elemento de angulo solido $rad^2$, elemento de flujo radiante $W$ und flujo radiante angular $W/rad^2$ como
| $ I = \displaystyle\frac{ d\Phi }{ d\Omega }$ |
se puede definir la radiancia como la fracci n de la densidad angular del flujo por elemento superficie con elemento de angulo solido $rad^2$, elemento de flujo radiante $W$ und flujo radiante angular $W/rad^2$ como
| $ L = \displaystyle\frac{ dI }{ dS }$ |
(ID 12473)
Si la presencia del agua es homog nea, sea en forma de vapor o de liquido, se tendr que la irradiancia se perder
$\displaystyle\frac{dL}{L}\propto dr$
Por ello la irradiancia ser
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
con
(ID 12470)
La ley de Lambert, con coeficiente de absorción $1/m$, distancia recorrida $m$ und radiancia $W/m^2 rad^2$
| $ \displaystyle\frac{d L }{d r } = - \alpha L $ |
se puede integrar dando la luminosidad en funci n de la distancia igual a
| $ L = L_0 e^{- \alpha r } $ |
(ID 12477)
Los valores del coeficiente de absorci n son mayores en el rango infrarrojo debido en parte a lo que se denomina la sustancia amarilla que corresponde a los restos de vida org nica. El coeficiente se va reduciendo en direcci n de largos de onda mayores que corresponden a el rango visible (VIS):

(ID 12478)
Los valores del coeficiente de absorci n en el rango visible (VIS) pasan por un m nimo creciendo para largos de onda mayores:

(ID 12479)
Si se compara el coeficiente de absorci n a distintas profundidades (o sea distintas presiones) se nota que en general se mantiene la forma pero se va reduciendo con la profundidad:

(ID 12480)
Si se analiza el origen del coeficiente de absorci n en el rango visible que ve que:
• en los largos de onda menores el efecto de la sustancia amarilla (restos de vida org nica) domina
• otros materiales en suspensi n tambi n tiene una contribuci n para largos de ondas menores
• el incremento para largo de ondas mayores es propio del agua

(ID 12481)
ID:(1537, 0)
