Benützer:
Schallgeschwindigkeit im Meer
Storyboard 
Die Schallgeschwindigkeit im Meer hängt von Druck, Temperatur und Salzgehalt ab.
ID:(1548, 0)
Schallgeschwindigkeit im Meer
Storyboard
Die Schallgeschwindigkeit im Meer hängt von Druck, Temperatur und Salzgehalt ab.
Variablen
Berechnungen
zu 
,
dann die Variable auswählen: 
zu 
Berechnungen
Variable
Gegeben
Berechnen
Ziel :
Gleichung
Zu verwenden
Gleichungen
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
Observando la imagen se nota que los senos de los angulos son respectivamente\\n\\n
$\sin\theta_i=\displaystyle\frac{c_i\Delta t}{d}$
y\\n\\n
$\sin\theta_e=\displaystyle\frac{c_e\Delta t}{d}$
\\n\\nSi se despeja en ambas ecuaciones la distancia
$d=\displaystyle\frac{c_i\Delta t}{\sin\theta_i}=\displaystyle\frac{c_e\Delta t}{\sin\theta_e}$
por lo que se tiene que
Da die Frequenz das Reziprokum der Zeit f r eine Schwingung ist:
$\nu=\displaystyle\frac{1}{T}$
bedeutet dies, dass die Lichtgeschwindigkeit gleich der Strecke ist, die in einer Schwingung zur ckgelegt wird, das ist die Wellenl nge, geteilt durch die ben tigte Zeit, das ist die Periode:
$c=\displaystyle\frac{\lambda}{T}$
Mit anderen Worten:
Da die Frequenz das Reziprokum der Zeit f r eine Schwingung ist:
$\nu=\displaystyle\frac{1}{T}$
bedeutet dies, dass die Lichtgeschwindigkeit gleich der Strecke ist, die in einer Schwingung zur ckgelegt wird, das ist die Wellenl nge, geteilt durch die ben tigte Zeit, das ist die Periode:
$c=\displaystyle\frac{\lambda}{T}$
Mit anderen Worten:
Beispiele
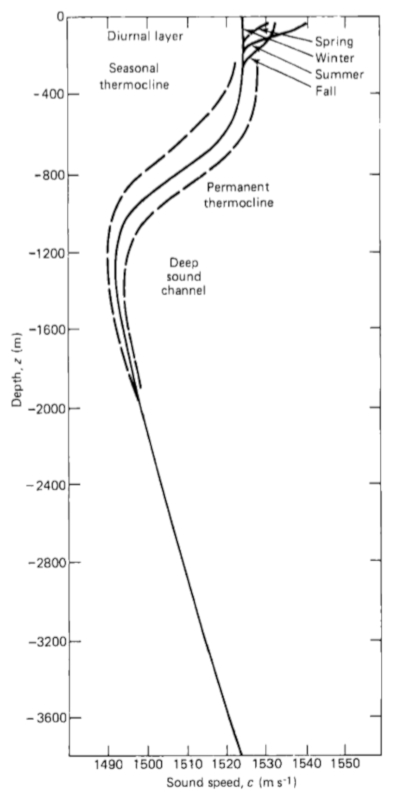
Die Schallgeschwindigkeit im Ozean variiert mit der Tiefe, wie in der Grafik dargestellt:
Die Form der Kurve kann je nach Jahreszeit variieren.
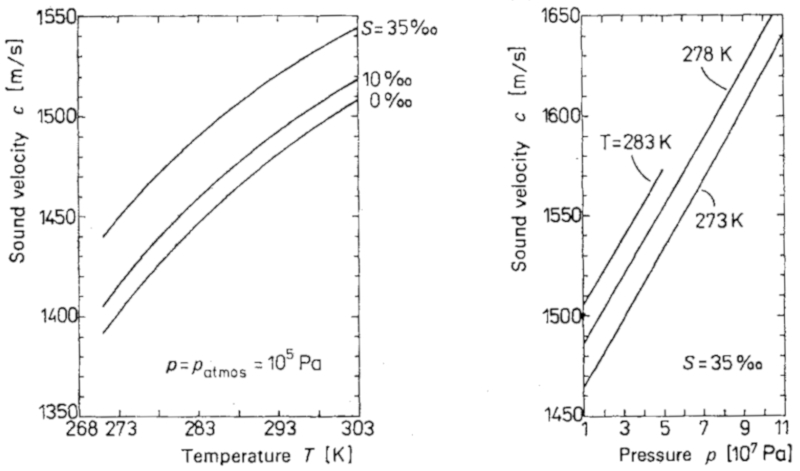
Die Schallgeschwindigkeit im Ozean h ngt von Temperatur und Druck ab, wie in der Grafik dargestellt:
Im Jahr 1977 entwickelten Clay und Medwin ein Modell zur Sch tzung der Schallgeschwindigkeit in Abh ngigkeit von Temperatur, Salinit t und Druck.
die Schallgeschwindigkeit ($c$) kann basierend auf die Presión hidrostatica ($p$), die Temperatur ($T$) und die Salzgehalt ($s$) mit folgendem Ausdruck gesch tzt werden:
wobei $c_i$ empirische Konstanten sind.
Referenz: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah und Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, Nr. 22, November 2017.
La relaci n entre los ngulos de incidencia y refractados indicados en la siguiente gr fica
se pueden escribir en funci n de la velocidad de la luz en cada medio
La relaci n entre los ngulos de incidencia y refractados indicados en la siguiente gr fica
se pueden escribir en funci n de la velocidad de la luz en cada medio
Im Jahr 1977 entwickelten Clay und Medwin ein Modell zur Sch tzung der Schallgeschwindigkeit in Abh ngigkeit von Temperatur, Salinit t und Druck.
die Schallgeschwindigkeit ($c$) kann basierend auf die Presión hidrostatica ($p$), die Temperatur ($T$) und die Salzgehalt ($s$) mit folgendem Ausdruck gesch tzt werden:
wobei $c_i$ empirische Konstanten sind.
Referenz: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah und Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, Nr. 22, November 2017.
Im Jahr 1977 entwickelten Clay und Medwin ein Modell zur Sch tzung der Schallgeschwindigkeit in Abh ngigkeit von Temperatur, Salinit t und Druck.
die Schallgeschwindigkeit ($c$) kann basierend auf die Presión hidrostatica ($p$), die Temperatur ($T$) und die Salzgehalt ($s$) mit folgendem Ausdruck gesch tzt werden:
wobei $c_i$ empirische Konstanten sind.
Referenz: "Study of Absorption loss effects on acoustic wave propagation in shallow water using different empirical Models", Yasin Yousif Al-Aboosi, Mustafa Sami Ahmed, Nor Shahida Mohd Shah und Nor Hisham Haji Khamis, ARPN Journal of Engineering and Applied Sciences, Vol. 12, Nr. 22, November 2017.
Eine Welle mit der Photon Frequency ($\nu$) steht ber die Lichtgeschwindigkeit ($c$) in Beziehung zu ERROR:8439, gem der folgenden Formel:
Diese Formel entspricht der mechanischen Beziehung, die besagt, dass die Geschwindigkeit einer Welle gleich ihrer Wellenl nge (zur ckgelegte Strecke) dividiert durch die Schwingungsperiode ist oder direkt proportional zur Frequenz (dem Kehrwert der Periode).
Eine Welle mit der Photon Frequency ($\nu$) steht ber die Lichtgeschwindigkeit ($c$) in Beziehung zu ERROR:8439, gem der folgenden Formel:
Diese Formel entspricht der mechanischen Beziehung, die besagt, dass die Geschwindigkeit einer Welle gleich ihrer Wellenl nge (zur ckgelegte Strecke) dividiert durch die Schwingungsperiode ist oder direkt proportional zur Frequenz (dem Kehrwert der Periode).
ID:(1548, 0)
