User:
Heat conduction mechanism
Image 
To understand how heat is conducted, you can think of a body as being represented by chains of springs that oscillate according to their temperature. If one end of the body has a higher temperature, the corresponding oscillation will also be greater. Since neighboring components oscillate to a lesser extent, they will be gradually affected, leading to the slow distribution of the oscillation/temperature along the chain, as depicted below:
Conduction will be more effective when there are more chains (cross-sectional area) present, and it will be slower as the chains become longer.
ID:(11188, 0)
Heat transport mechanisms
Model
Variables
Calculations
to 
,
then, select the variable: 
to 
Calculations
Variable
Given
Calculate
Target :
Equation
To be used
Equations
Since the heat transported ($dQ$) is a function of the conductor length ($L$), the section ($S$), the time variation ($dt$), the temperature difference in the conductor ($\Delta T_0$), and the thermal conductivity ($\lambda$) according to the following equation:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
With the equation for the heat flow rate ($q$) defined as:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
In the infinitesimal case, where the conductor length ($L$) reduces to ERROR:10179.1 and the temperature difference in the conductor ($\Delta T_0$) becomes the temperature variation ($dT$), the equation simplifies to:
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
(ID 15132)
The quantity of the heat transported ($dQ$) through ERROR:10179.1 can be calculated using the heat flow rate ($q$) and the time variation ($dt$) with the section ($S$) through the following equation:
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Since the heat flow rate ($q$) with the temperature variation ($dT$) and the thermal conductivity ($\lambda$) is defined as:
| $ q = - \lambda \displaystyle\frac{dT}{dz}$ |
Therefore,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
On the other hand, we can relate the heat supplied to liquid or solid ($\Delta Q$) with the mass ($M$), the specific heat ($c$), and the temperature variation ($\Delta T$) through the equation:
| $ \Delta Q = M c \Delta T$ |
In this case, with the volume Variation ($\Delta V$), the equation becomes:
$dQ=\rho dV c dT = \rho c S dz dT$
And finally, we have:
| $ \displaystyle\frac{\partial T}{\partial t}=\displaystyle\frac{\lambda}{\rho c}\displaystyle\frac{\partial^2 T}{\partial z^2}$ |
(ID 15134)
Examples
(ID 15274)
In the case of a solid, and similarly for a liquid, we can describe the system as a structure of atoms held together by something that behaves like a spring. When both ends have temperatures of ERROR:10165.1, with the inner surface temperature ($T_{is}$) and the outer surface temperature ($T_{es}$):
| $ \Delta T_0 = T_{is} - T_{es} $ |
The temperature difference implies that the atoms at the ends oscillate differently; atoms in the high-temperature zone will have a greater amplitude in their oscillations compared to the atoms in the low-temperature zone.
However, this difference will gradually lead to the entire chain oscillating in such a way that, in the end, the amplitude will vary along the path, from the highest values where the temperature is also higher, to the lowest values in the lower-temperature zone.
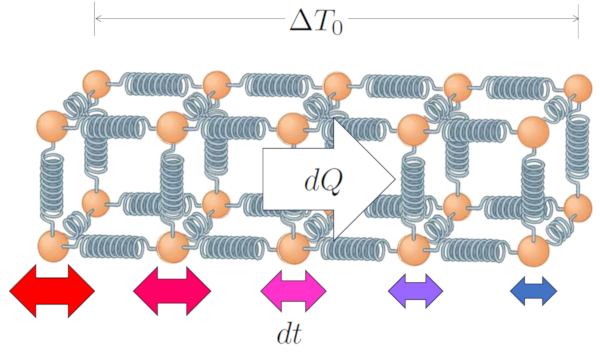
In this way, the temperature difference in the conductor ($\Delta T_0$) leads to ERROR:10159.1 in ERROR:10160.1.
(ID 15234)
To understand how heat is conducted, you can think of a body as being represented by chains of springs that oscillate according to their temperature. If one end of the body has a higher temperature, the corresponding oscillation will also be greater. Since neighboring components oscillate to a lesser extent, they will be gradually affected, leading to the slow distribution of the oscillation/temperature along the chain, as depicted below:
Conduction will be more effective when there are more chains (cross-sectional area) present, and it will be slower as the chains become longer.
(ID 11188)
Heat transfer and conduction models suggest that it is possible to develop a relationship that incorporates all three mechanisms together. This equation should take into account the heat transported ($dQ$), the time variation ($dt$), the temperature difference ($\Delta T$), the section ($S$), and the total transport coefficient (multiple medium, two interfaces) ($k$):
Mathematically, this can be expressed as follows:
| $ q = k \Delta T $ |
(ID 15241)
One of the effects of heat transfer from a conductor to an external medium is the heating of the medium near the interface, creating an interference zone in the transmission. This decreases the efficiency of the transfer and tends to form an insulating layer that reduces the flow of energy.
However, this effect can change in the presence of wind. The wind can remove the layer of high-temperature atoms and molecules, enhancing the efficiency of heat transfer. This suggests that the transmission coefficient ($\alpha$) is influenced by the mean speed ($v_m$) [1,2]:
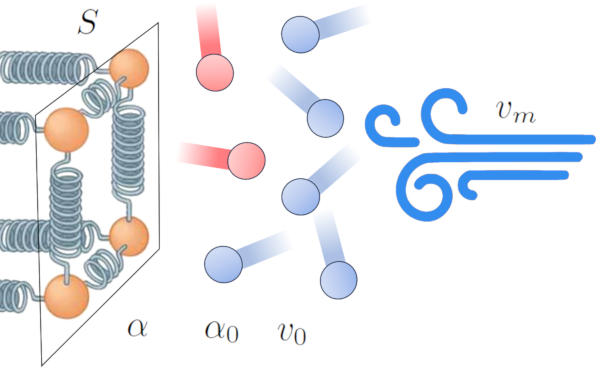
In this context, we model the relationship based on ERROR:9844,0 and a reference factor of the media reference speed ($v_0$).
The mathematical relationship that describes this phenomenon for a gas with the transmission coefficient in gases, dependent on speed ($\alpha_{gv}$), the mean speed ($v_m$), the transmission coefficient in gases, independent of speed ($\alpha_{g0}$), and the transmission coefficient gas velocity factor ($v_{g0}$) is:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
And for a liquid with the transmission coefficient dependent on the speed ($\alpha_{wv}$), the mean speed ($v_m$), the transmission coefficient Independent of the speed ($\alpha_{w0}$), and the factor velocidad del coefiente de transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
This illustrates how wind can significantly influence the efficiency of heat transfer between a conductor and an external medium.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (On Fluid Movement with Very Little Friction), Ludwig Prandtl, 1904 [2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (The Dependence of the Heat Transfer Coefficient on the Length of the Pipe), Wilhelm Nusselt, 1910
(ID 3620)
(ID 15333)
ID:(1512, 0)