Utilizador:
Trabalho
Storyboard 
O trabalho depende da maneira como o processo ocorre. Por exemplo, representa a energia necessária para aplicar uma força específica e mover um corpo ao longo de uma certa distância, ou a pressão que deve ser mantida sobre um gás para permitir que ele se expanda por um volume específico.
ID:(1470, 0)
Mecanismos
Iframe
Na termodinâmica, o trabalho é a energia transferida para ou de um sistema através de uma força que atua ao longo de uma distância. Isso pode ocorrer de várias formas, como o trabalho mecânico, onde um gás em um cilindro com um pistão se expande e move o pistão, ou o trabalho elétrico, que envolve a transferência de energia por meio de forças elétricas. O conceito de trabalho é crucial para entender as trocas de energia e os processos. Ele é representado matematicamente, frequentemente envolvendo mudanças de pressão e volume no sistema. Segundo a primeira lei da termodinâmica, a mudança na energia interna de um sistema é igual ao calor adicionado ao sistema menos o trabalho realizado pelo sistema em seus arredores. O trabalho é essencial em vários processos, incluindo processos isotérmicos, adiabáticos, isobáricos e isocóricos, e é fundamental em aplicações como motores térmicos e refrigeradores, onde desempenha um papel-chave na conversão de calor em trabalho ou na utilização do trabalho para transferir calor.
Mecanismos
ID:(15247, 0)
Conversor trabalho-calor
Descrição
A conversão de trabalho em energia é estudada através da geração de calor por meio do atrito. Para isso, envolve-se uma faixa metálica ao redor de um cilindro que contém água e um termômetro. Ao girar a manivela, o atrito gera calor, levando ao aquecimento da água. Se medirmos a força aplicada, o número de voltas realizadas e o raio do cilindro, é possível estimar a distância percorrida, o que nos permite estimar a energia como o produto da força pela distância.
ID:(1884, 0)
Pressão e trabalho
Descrição
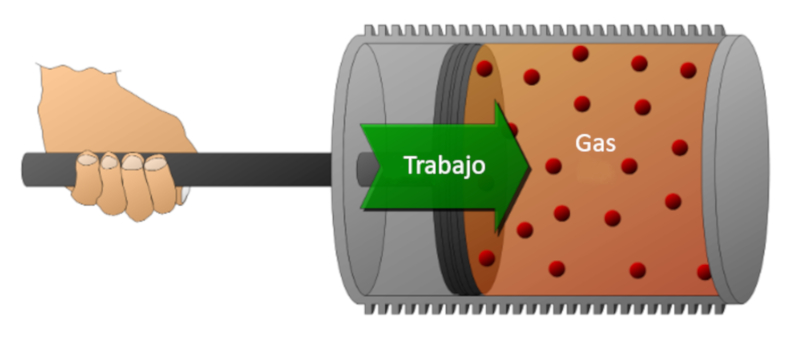
Consideremos um gás em um cilindro onde um pistão pode se deslocar. Se o pistão for movido, é possível reduzir o volume, comprimindo o gás. Para realizar essa compressão, é necessária uma energia que é igual à força exercida pelo gás multiplicada pela distância percorrida pelo pistão. Essa energia também pode ser representada em função da pressão, já que a pressão é definida pela força e pela área do pistão.
O trabalho pode ser realizado pelo sistema (compressão) ou pelo sistema sobre o meio externo (expansão).
Uma vez que la força mecânica ($F$) dividido por la seção ($S$) é igual a la pressão ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
e la variação de volume ($dV$) com o distância percorrida ($dx$) é igual a:
| $ \Delta V = S \Delta s $ |
A equação para o diferencial de trabalho impreciso ($\delta W$) pode ser expressa como:
| $ \delta W = F dx $ |
Portanto, ela pode ser escrita como:
| $ \delta W = p dV $ |
ID:(11126, 0)
Pressão e trabalho sobre um gás
Descrição
Ao movimentar-se dentro do cilindro, o pistão atua como uma raquete de tênis, conferindo energia cinética às moléculas e aumentando sua velocidade. À medida que essas moléculas adquirem maior velocidade, elas transferem um impulso maior às paredes, resultando em um aumento de pressão.
ID:(11127, 0)
Pressão e trabalho em um líquido/sólido
Descrição
No caso de um líquido ou sólido, uma força externa desloca as partículas do material, o que afeta a energia potencial das ligações entre elas. Isso pode ser imaginado como pequenas molas sendo comprimidas, aumentando assim sua energia potencial.
ID:(11128, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \delta W = F dx $
dW = F * dx
$ \delta W = p dV $
dW = p * dV
$ W = \displaystyle\int_{V_1}^{V_2}p\,dV$
W = @INT( p , V , V_1 , V_2 )
ID:(15306, 0)
Trabalho
Equação
A relação entre o trabalho e as nossas ações está ligada à dependência de o diferencial de trabalho impreciso ($\delta W$) em relação à distância percorrida. Se considerarmos uma força mecânica ($F$) para mover um objeto ao longo de um distância percorrida ($dx$), a energia necessária pode ser expressa da seguinte forma:
| $ \delta W = F dx $ |
A notação $\delta W$ é usada para indicar a variação do trabalho, ao contrário de $dW$, que nos lembra que o seu valor depende do processo de variação do comprimento $dx$. Um exemplo disso ocorreria se o deslocamento ocorresse em um gás e uma mudança nele ocorresse, nesse caso:
$\delta W < Fdx$
ID:(3202, 0)
Pressão e trabalho
Equação
O diferencial de trabalho impreciso ($\delta W$) é igual a la pressão ($p$) multiplicado por la variação de volume ($dV$):
| $ \delta W = p dV $ |
Uma vez que la força mecânica ($F$) dividido por la seção ($S$) é igual a la pressão ($p$):
| $ p \equiv\displaystyle\frac{ F }{ S }$ |
e la variação de volume ($dV$) com o distância percorrida ($dx$) é igual a:
| $ \Delta V = S \Delta s $ |
A equação para o diferencial de trabalho impreciso ($\delta W$) pode ser expressa como:
| $ \delta W = F dx $ |
Portanto, ela pode ser escrita como:
| $ \delta W = p dV $ |
ID:(3468, 0)
Trabalho realizado
Equação
O trabalho eficaz ($W$) é igual à integral de la pressão ($p$) em relação a o volume ($V$) de $V_1$ a $V_2$. Isso representa o trabalho realizado pela máquina, que pode ser expresso como:
| $ W = \displaystyle\int_{V_1}^{V_2}p\,dV$ |
ID:(10253, 0)
0
Video
Vídeo: Trabalho