User:
Internal Energy
Storyboard 
The internal energy of a system consists of kinetic energy and potential energy. Kinetic energy is associated with heat and can be linked to the oscillations of atoms around their equilibrium points. On the other hand, potential energy is associated with the work that the system is capable of performing.
ID:(1469, 0)
Mechanisms
Iframe
Internal energy is the total energy contained within a thermodynamic system due to the kinetic and potential energies of its molecules. It includes the energy from molecular motion (translational, rotational, and vibrational) and the energy from intermolecular interactions and chemical bonds. Internal energy is a state function, meaning it depends only on the current state of the system, not on how the system reached that state. Changes in internal energy occur when heat is added to or removed from the system or when work is done on or by the system. This concept is fundamental in thermodynamics, describing energy changes in processes such as isothermal, adiabatic, isobaric, and isochoric processes. Internal energy helps determine equilibrium states and system stability, as systems tend to move towards states with lower internal energy. It provides a comprehensive measure of all microscopic forms of energy within a system, essential for understanding energy transformations in various processes.
Mechanisms
ID:(15245, 0)
Kinetic energy
Concept
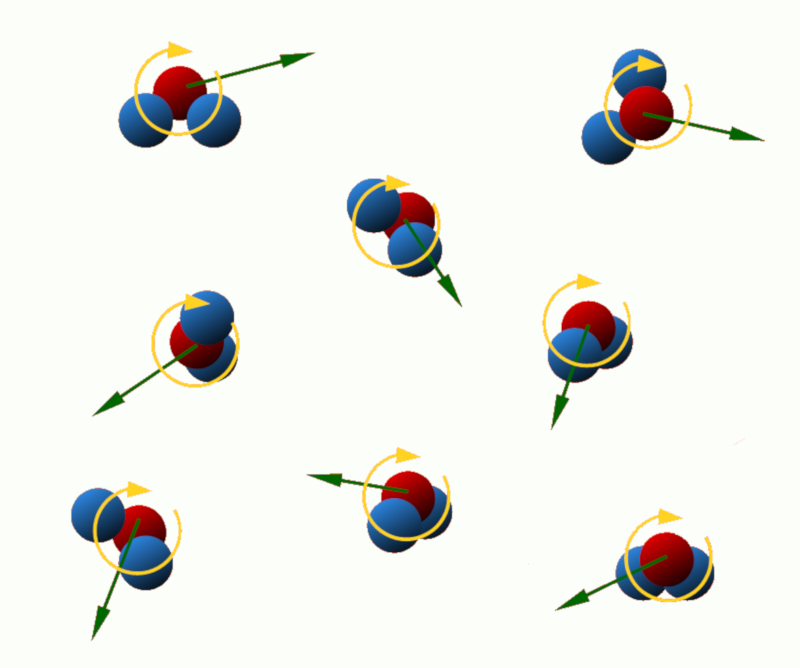
Translational kinetic energy: This energy is associated with the linear motion of the particles in the system. The higher the translational velocity of the particles, the greater their translational kinetic energy.
Rotational kinetic energy: Some particles, such as atoms or molecules, can rotate around an axis. This rotation is associated with the rotational kinetic energy, which depends on the mass and angular velocity of the particles.
ID:(11122, 0)
Link energy
Concept
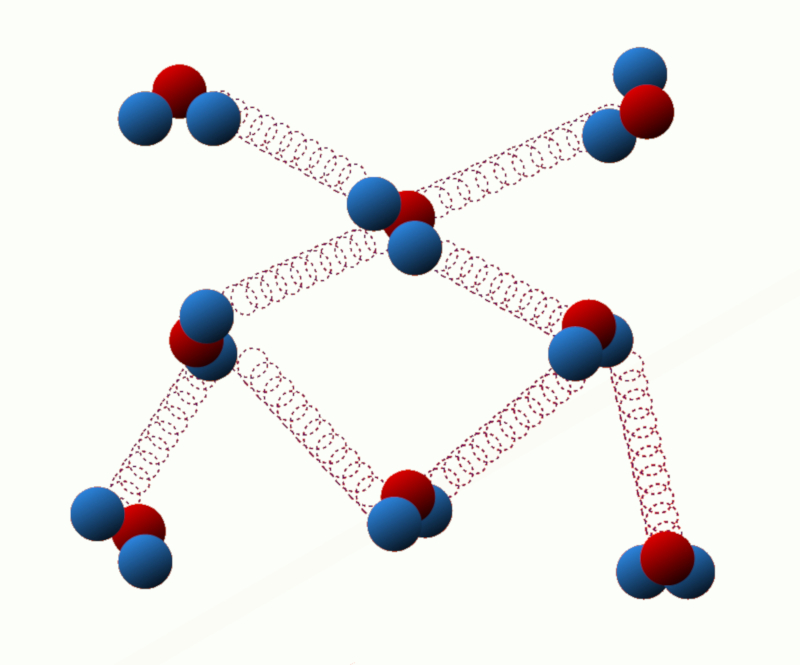
Potential energy of binding: This energy is related to the interaction forces between the particles of the system. For example, in a solid, the binding energy is due to the attractive forces between neighboring atoms or molecules.
ID:(11123, 0)
Chemical energy
Concept
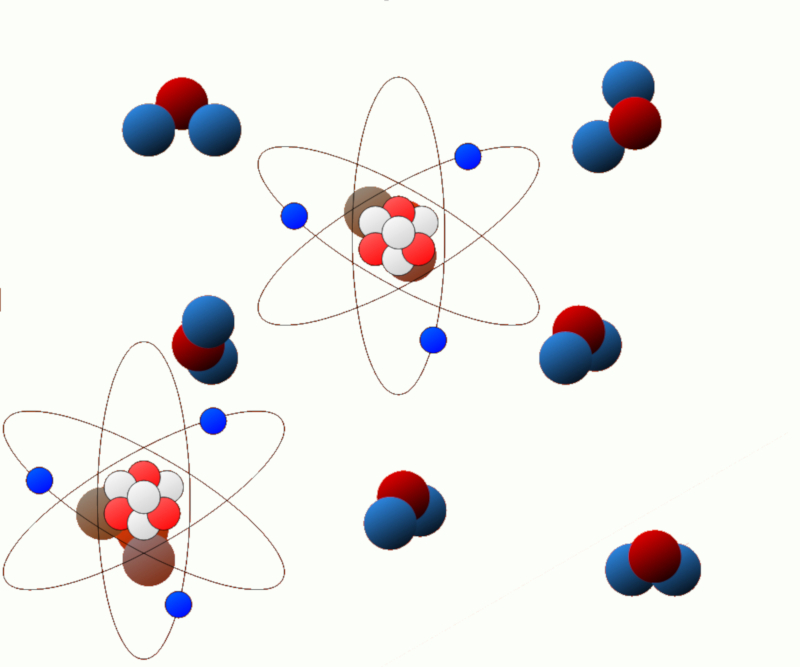
Excitation energy: Some systems can undergo changes in their energy state, such as when electrons in an atom or molecule are excited. The energy associated with these excited states is known as excitation energy.
ID:(11124, 0)
Excitation energy
Concept
Chemical energy (electrical energy): In chemical systems, chemical reactions can release or absorb energy. This energy is known as chemical energy and is related to the chemical bonds present in molecules.
ID:(11125, 0)
Internal energy
Concept
The internal energy is the total energy possessed by the particles that make up a system. These energies include:
• Translational kinetic energy: This energy is associated with the linear motion of the particles in the system. The higher the translational velocity of the particles, the greater their translational kinetic energy.
• Rotational kinetic energy: Some particles, such as atoms or molecules, can rotate around an axis. This rotation is associated with the rotational kinetic energy, which depends on the mass and angular velocity of the particles.
• Potential energy of binding: This energy is related to the interaction forces between the particles of the system. For example, in a solid, the binding energy is due to the attractive forces between neighboring atoms or molecules.
• Chemical energy (electrical energy): In chemical systems, chemical reactions can release or absorb energy. This energy is known as chemical energy and is related to the chemical bonds present in molecules.
• Excitation energy: Some systems can undergo changes in their energy state, such as when electrons in an atom or molecule are excited. The energy associated with these excited states is known as excitation energy.
ID:(11121, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ E = K + V $
E = K + V
$ K = K_t + K_r $
K = K_t + K_r
$ K_r =\displaystyle\frac{1}{2} I \omega ^2$
K_r = I * omega ^2/2
$ K_t =\displaystyle\frac{1}{2} m_i v ^2$
K_t = m_i * v ^2/2
ID:(15304, 0)
Translational Kinetic Energy
Equation
In the case of studying translational motion, the definition of energy
| $ dW = \vec{F} \cdot d\vec{s} $ |
is applied to Newton's second law
| $ F = m_i a $ |
resulting in the expression
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
The energy required for an object to transition from velocity $v_1$ to velocity $v_2$ can be calculated using the definition with
| $ dW = \vec{F} \cdot d\vec{s} $ |
Using the second law of Newton, this expression can be rewritten as
$\Delta W = m a \Delta s = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s$
Employing the definition of velocity with
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
we obtain
$\Delta W = m\displaystyle\frac{\Delta v}{\Delta t}\Delta s = m v \Delta v$
where the difference in velocities is
$\Delta v = v_2 - v_1$
Furthermore, the velocity itself can be approximated by the average velocity
$v = \displaystyle\frac{v_1 + v_2}{2}$
Using both expressions, we arrive at
$\Delta W = m v \Delta v = m(v_2 - v_1)\displaystyle\frac{(v_1 + v_2)}{2} = \displaystyle\frac{m}{2}(v_2^2 - v_1^2)$
Thus, the change in energy is given by
$\Delta W = \displaystyle\frac{m}{2}v_2^2 - \displaystyle\frac{m}{2}v_1^2$
In this way, we can define kinetic energy
| $ K_t =\displaystyle\frac{1}{2} m_i v ^2$ |
ID:(3244, 0)
Kinetic Energy of Rotation
Equation
In the case being studied of translational motion, the definition of energy
| $ \Delta W = T \Delta\theta $ |
is applied to Newton's second law
| $ T = I \alpha $ |
resulting in the expression
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
The energy required for an object to change its angular velocity from $\omega_1$ to $\omega_2$ can be calculated using the definition
| $ \Delta W = T \Delta\theta $ |
Applying Newton's second law, this expression can be rewritten as
$\Delta W=I \alpha \Delta\theta=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta$
Using the definition of angular velocity
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
we get
$\Delta W=I\displaystyle\frac{\Delta\omega}{\Delta t}\Delta\theta=I \omega \Delta\omega$
The difference in angular velocities is
$\Delta\omega=\omega_2-\omega_1$
On the other hand, angular velocity itself can be approximated with the average angular velocity
$\omega=\displaystyle\frac{\omega_1+\omega_2}{2}$
Using both expressions, we obtain the equation
$\Delta W=I \omega \Delta \omega=I(\omega_2-\omega_1)\displaystyle\frac{(\omega_1+\omega_2)}{2}=\displaystyle\frac{I}{2}(\omega_2^2-\omega_1^2)$
Thus, the change in energy is given by
$\Delta W=\displaystyle\frac{I}{2}\omega_2^2-\displaystyle\frac{I}{2}\omega_1^2$
This allows us to define kinetic energy as
| $ K_r =\displaystyle\frac{1}{2} I \omega ^2$ |
ID:(3255, 0)
Total Kinetic Energy
Equation
Kinetic energy can be of translation and/or rotation. Therefore, the total kinetic energy is the sum of both:
| $ K = K_t + K_r $ |
ID:(3686, 0)
Total Energy
Equation
The total energy corresponds to the sum of the total kinetic energy and the potential energy:
| $ E = K + V $ |
ID:(3687, 0)