Utilisateur:
Entropie
Storyboard 
L'entropie est la partie de l'énergie dans un système qui ne peut pas être utilisée pour effectuer un travail. D'un point de vue microscopique, elle est liée au nombre de configurations possibles que le système peut adopter. Un plus grand nombre de ces configurations est associé à une augmentation du désordre du système et à une diminution de la probabilité que celui-ci retourne à un état antérieur, réduisant ainsi la possibilité de réversibilité du système.
ID:(1471, 0)
Mécanismes
Iframe
L'entropie physique est un concept fondamental en thermodynamique et en mécanique statistique qui représente le degré de désordre ou de hasard dans un système. Elle mesure le nombre de façons spécifiques dont un système thermodynamique peut être organisé, reflétant la quantité d'incertitude ou le nombre de microétats possibles correspondant à un état macroscopique donné. L'entropie quantifie le désordre, une entropie plus élevée indiquant un plus grand désordre. Selon la deuxième loi de la thermodynamique, l'entropie d'un système isolé ne diminue jamais, ce qui signifie que les processus naturels tendent à évoluer vers un état de désordre maximal. L'entropie mesure également l'irréversibilité des processus, les processus spontanés augmentant l'entropie de l'univers. Elle est un facteur clé pour déterminer l'efficacité des machines thermiques et des réfrigérateurs, comprendre le comportement des systèmes biologiques et étudier l'évolution de l'univers. Essentiellement, l'entropie est une mesure de l'imprévisibilité et de la dispersion de l'énergie dans un système, fournissant des informations sur la tendance naturelle au désordre et les limitations de la conversion de l'énergie.
Mécanismes
ID:(15246, 0)
Types de variables
Description
Si nous considérons l'équation de différentiel de travail inexact ($\delta W$) avec a force mécanique ($F$) et le distance parcourue ($dx$) :
| $ \delta W = F dx $ |
sous sa forme de a pression ($p$) et le volume ($V$) :
| $ \delta W = p dV $ |
Le travail joue le rôle d'un potentiel, tandis que a pression ($p$) agit comme une 'force généralisée', et le volume ($V$) sert de chemin, une sorte de 'variable indépendante'. Si nous organisons ces concepts dans une matrice pour les paramètres que nous avons discutés jusqu'à présent, nous obtenons :
| Potentiel thermodynamique | Force généralisée | Variable indépendante |
| Extensive | Intensive | Extensive |
| $\delta W$ | $p$ | $dV$ |
| $\delta Q$ | $T$ | $?$ |
Dans ce contexte, nous voyons que pour la ligne a variation de chaleur ($\delta Q$), nous avons la variable a température absolue ($T$), mais nous manquons d'une variable indépendante extensive. Nous appellerons cela entropie et la noterons avec la lettre $S$.
ID:(11183, 0)
Variáveis intensivas e extensivas
Description
Il existe des variables qui sont associées à des quantités et d'autres qui sont associées à des propriétés.
• Les premières sont appelées variables extensives, car elles peuvent être étendues ou augmentées en proportion de la quantité de substance présente. Des exemples de variables extensives incluent le volume, la masse, la charge électrique, la chaleur, etc.
• En revanche, les secondes sont appelées variables intensives, qui représentent des propriétés qui ne dépendent pas de la quantité de substance présente. Ces propriétés ne changent pas lorsque la quantité de substance change. Des exemples de variables intensives incluent la densité, la pression, la température, etc.
ID:(11182, 0)
Entropie et changement de phase
Description
Si l'entropie est estimée en fonction de la température, les observations suivantes peuvent être faites :
• Dans chaque phase (solide, liquide, gazeux), l'entropie a tendance à augmenter légèrement avec la température.
• Lors de chaque transition de phase, il y a un saut significatif dans l\'entropie.
Cela peut être représenté de la manière suivante :
Ainsi, on peut comprendre l\'entropie comme une mesure moyenne des degrés de liberté qu\'un système possède. Alors que dans chaque phase, l\'entropie augmente progressivement car quelques degrés de liberté supplémentaires sont \\"libérés\\", lors des transitions de phase, l\'augmentation de l\'entropie est importante. Dans un solide, de multiples liaisons restreignent le mouvement des atomes, ce qui limite les degrés de liberté. Dans un liquide, de nombreuses liaisons sont rompues, créant de nouvelles libertés qui permettent les mouvements relatifs et entraînent de nombreux nouveaux degrés de liberté. Enfin, lors de la transition vers la phase gazeuse, toutes les liaisons sont perdues et chaque particule a ses trois degrés de liberté. À mesure que la température augmente, les particules peuvent tourner et osciller, introduisant de nouveaux degrés de liberté et des augmentations supplémentaires de l\'entropie.
ID:(11187, 0)
Entropie et irréversibilité
Description
Si nous considérons deux systèmes identiques, l'un avec une température $T_1$ et l'autre avec une température $T_2$, leurs entropies peuvent être calculées à l'aide de l'équation impliquant a entropie ($S$), a température absolue ($T$), a chaleur spécifique de l'échantillon ($C$), a entropie de base ($S_0$), et a température de base ($T_0$) :
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
Par conséquent, les entropies seront :
$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$
et
$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Si les deux systèmes sont mélangés, leur température sera la température moyenne :
$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$
Par conséquent, l'entropie du nouveau système sera :
$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$
L'entropie du nouveau système est supérieure à la somme des entropies individuelles :
$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
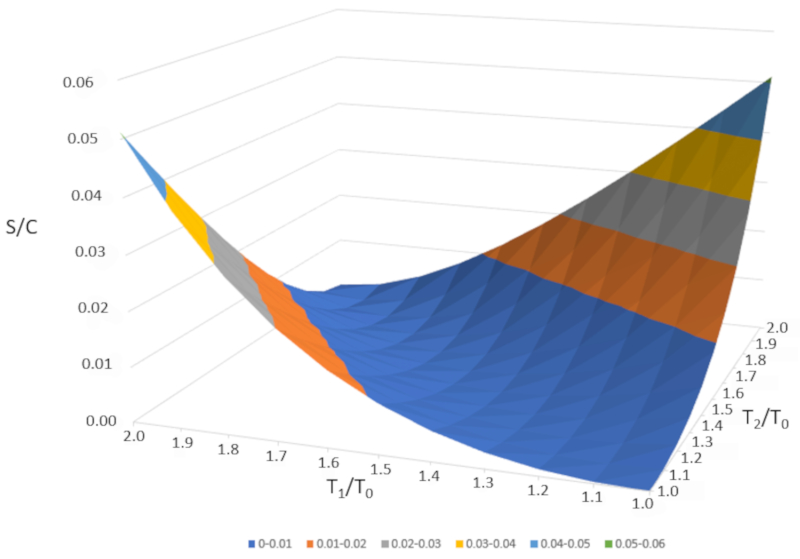
Si nous représentons graphiquement $\Delta S/C$ en fonction de $T_1/T_0$ et $T_2/T_0," nous obtenons la figure suivante :
$\Delta S/C$ est presque nul si les températures sont très similaires ($T_1\sim T_2$). Cependant, si les températures sont différentes, l'entropie augmentera toujours. Si nous étudions cela dans d'autres systèmes, nous constaterons que chaque fois qu'un changement irréversible se produit, l'entropie augmente. Le mélange est irréversible, ce qui signifie que le système ne reviendra pas à son état initial sans intervention externe. En d'autres termes, le système ne se séparera pas spontanément en deux sous-systèmes avec des températures complètement différentes.
ID:(11186, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \delta Q = T dS $
dQ = T * dS
$ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$
S = S_0 + C *log( T / T_0 )
ID:(15305, 0)
Deuxième loi de la thermodynamique
Équation
Le différence de chaleur inexacte ($\delta Q$) est égal à A température absolue ($T$) fois a variation d'entropie ($dS$) :
| $ \delta Q = T dS $ |
ID:(9639, 0)
Calcul d'entropie
Équation
A entropie ($S$) est une fonction de a température absolue ($T$) avec a entropie de base ($S_0$) et a température de base ($T_0$) selon :
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
La relation de a variation de chaleur ($\delta Q$) avec a température absolue ($T$) et a variation d'entropie ($dS$) peut être exprimée comme suit :
| $ \delta Q = T dS $ |
Lorsque nous combinons cela avec la relation entre a variation de chaleur ($\Delta Q$), a chaleur spécifique de l'échantillon ($C$) et a variation de température ($\Delta T$) :
| $ \Delta Q = C \Delta T $ |
Nous obtenons cette relation dans la limite infinitésimale, où :
$\delta Q = C dT = T dS$
Après intégration, cela nous conduit à l'équation suivante :
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
avec la condition que a entropie de base ($S_0$) soit inférieur à A température de base ($T_0$).
ID:(11185, 0)