Usuario:
Interferencia de la luz de dos Fuentes
Storyboard 
Cuando se superponen luz de dos fuentes o ranuras se observan puntos en el espacio en que existe interferencia constructiva y otros destructiva generando zonas de mayor intensidad o intensidad nula.
ID:(1271, 0)
El concepto de interferencia
Definición
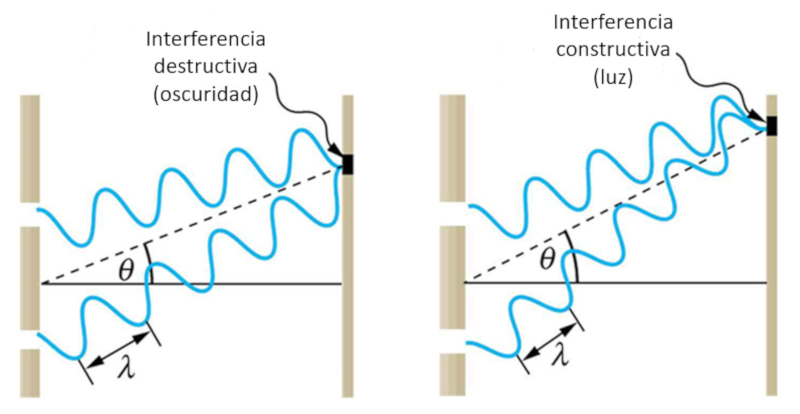
La interferencia ocurre cuando dos haces se superponen en un punto del espacio y con ello sus amplitudes se suman. Esto puede llevar a
• ambas tienen fases similares con lo que sus amplitudes son ambas positivas o negativas lo que lleva a una interferencia constructiva y a un aumento de la señal
• las fases difieren de modo que los signos de las amplitudes son mayormente distintos con lo que la interferencia es destructiva y la señal se reduce e incluso puede anularse
ID:(12495, 0)
El caso de dos rentijas
Imagen
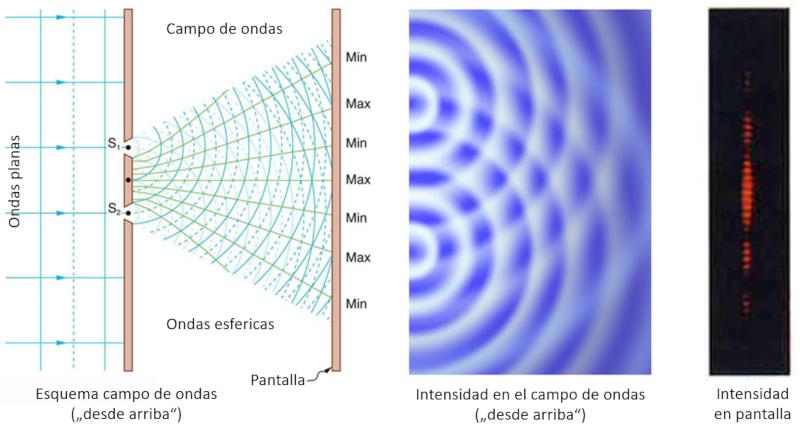
Cuando se tienen dos rendijas se puede observar como la onda plana pasa a generar dos ondas esféricas que generan un campo de onda en que se observan las distintas interferencias. Si se localiza a alguna distancia una pantalla se puede observar el perfil de dichas interferencias creándose casos de interferencia constructiva como destructiva:
ID:(12496, 0)
Calculo de la interferencia en la pantalla
Nota
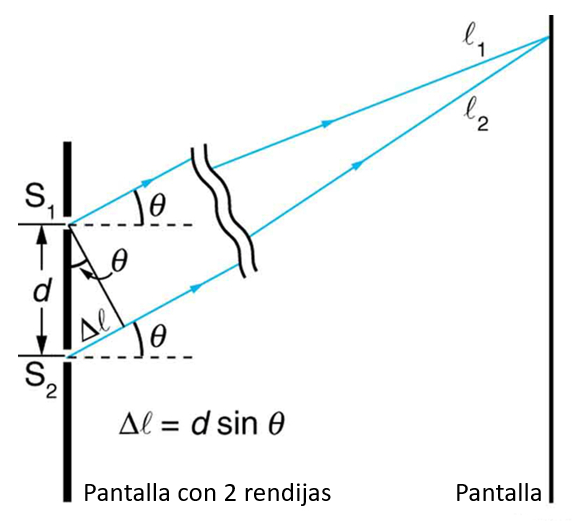
Si se asume que la pantalla se encuentra a una distancia mucho mayor que aquella entre ambas fuentes (rendijas) se puede estimar el desface de ambas señales en forma relativamente simple:
ID:(12497, 0)
Patrón de interferencia
Cita
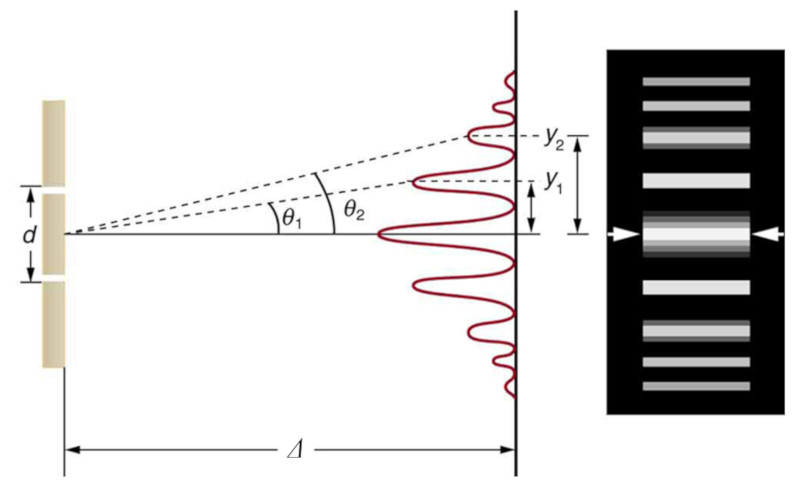
Si se diagrama la intensidad registrada en la pantalla se vera lo que se denomina el típico patrón de interferencia:
ID:(12498, 0)
Interferencia de la luz de dos Fuentes
Storyboard
Cuando se superponen luz de dos fuentes o ranuras se observan puntos en el espacio en que existe interferencia constructiva y otros destructiva generando zonas de mayor intensidad o intensidad nula.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
La interferencia ocurre cuando dos haces se superponen en un punto del espacio y con ello sus amplitudes se suman. Esto puede llevar a
• ambas tienen fases similares con lo que sus amplitudes son ambas positivas o negativas lo que lleva a una interferencia constructiva y a un aumento de la se al
• las fases difieren de modo que los signos de las amplitudes son mayormente distintos con lo que la interferencia es destructiva y la se al se reduce e incluso puede anularse
Cuando se tienen dos rendijas se puede observar como la onda plana pasa a generar dos ondas esf ricas que generan un campo de onda en que se observan las distintas interferencias. Si se localiza a alguna distancia una pantalla se puede observar el perfil de dichas interferencias cre ndose casos de interferencia constructiva como destructiva:
Si se asume que la pantalla se encuentra a una distancia mucho mayor que aquella entre ambas fuentes (rendijas) se puede estimar el desface de ambas se ales en forma relativamente simple:
Si se diagrama la intensidad registrada en la pantalla se vera lo que se denomina el t pico patr n de interferencia:
Para que la interferencia sea constructiva es necesario que la diferencia de camino sea un m ltiplo de el largo de onda\\n\\n
$\Delta l = n \lambda$
\\n\\nPor ello, como el largo es el cateto opuesto de un triangulo en que la hipotenusa es igual a la distancia entre ambas fuentes o rendijas se tiene\\n\\n
$\Delta l = d \sin\theta$
De ambas ecuaciones se tiene entonces que
Para que la interferencia sea destructiva es necesario que la diferencia de camino sea un m ltiple mas un medio del largo de onda\\n\\n
$\Delta l =\left( n + \displaystyle\frac{1}{2}\right) \lambda$
\\n\\nPor ello, como el largo es el cateto opuesto de un triangulo en que la hipotenusa es igual a la distancia entre ambas fuentes o rendijas se tiene\\n\\n
$\Delta l = d \sin\theta$
De ambas ecuaciones se tiene entonces que
Con la distancia
$\tan\theta_n = \displaystyle\frac{y_n}{\Delta}$
\\n\\nPara ngulos peque os la funci n tangente se puede aproximar por el seno\\n\\n
$ \tan \theta_n \sim \sin \theta_n $
por lo que la posici n de los m ximo es
por lo que las posiciones de los m ximos es
Si que existe un desfase
se tendr que la intensidad es igual a
La diferencia de fase de da por la diferencia en los caminos recorridos. Si se denotan se tendra que
ID:(1271, 0)