mechanisms

La fuerza experimentada por un cuerpo que se desplaza con una velocidad de ERROR:6029.1 en un medio, y que est caracterizado por la constante de fuerza viscosa ($b$), es la fuerza viscosa ($F_v$), como se describe por la ecuaci n:

equation=3243

Para comprender el papel de la constante de fuerza viscosa ($b$), es importante recordar que la viscosidad es una medida de c mo se difunde el momento, es decir, la velocidad de las mol culas. En otras palabras, la constante de fuerza viscosa ($b$) es la medida en la que el cuerpo pierde energ a al transferirla al medio y al acelerar las mol culas, entreg ndoles energ a. Por lo tanto, la constante de fuerza viscosa ($b$) es proporcional a la viscosidad.

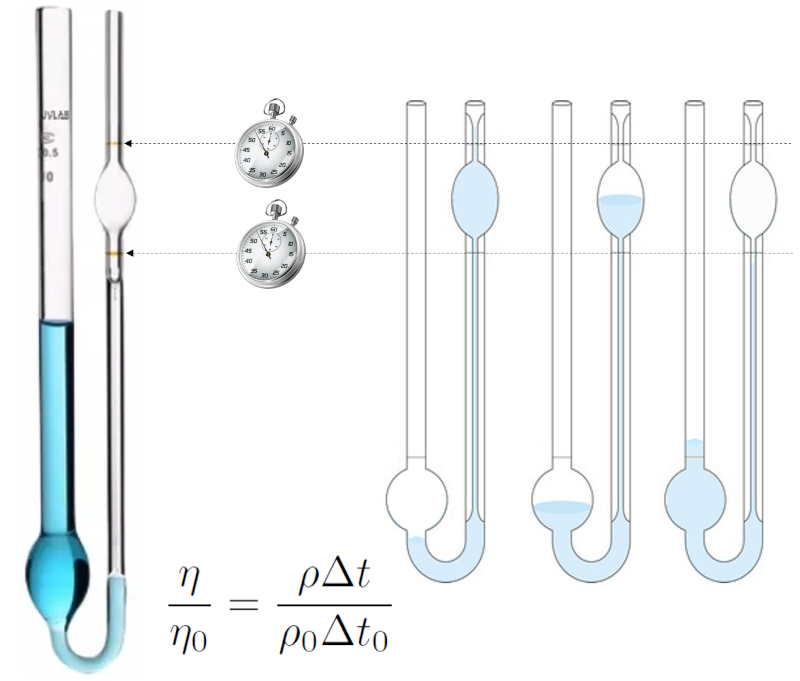
El m todo de medici n de viscosidad de Ostwald se basa en el comportamiento de un l quido que fluye por un tubo de radio peque o (capilar).

Se introduce el l quido, se succiona para que su nivel sobrepase la marca superior y luego se deja escurrir, midiendo el tiempo que el nivel tarda en pasar del nivel superior al inferior.

El experimento se realiza primero con un l quido para el cual se conoce la viscosidad y densidad (por ejemplo, agua destilada), y luego con el l quido para el cual se busca determinar la viscosidad. Si las condiciones son iguales, el l quido que fluya en ambos casos ser similar, y con ello, el tiempo ser proporcional a la densidad dividida por la viscosidad. As , se puede establecer una ecuaci n de comparaci n entre ambas viscosidades:

image

En el caso de un cuerpo cayendo en un medio viscoso, la ecuaci n de movimiento es una ecuaci n de la velocidad ($v$) en funci n de el tiempo ($t$) con la masa inercial ($m_i$) y la constante de fuerza viscosa ($b$):

equation=14499

Esto se obtiene con la tiempo de viscosidad y masa inercial ($\tau_i$)

equation=15548

Integrando con tiempo inicial nulo y la velocidad inicial ($v_0$),

equation=14500

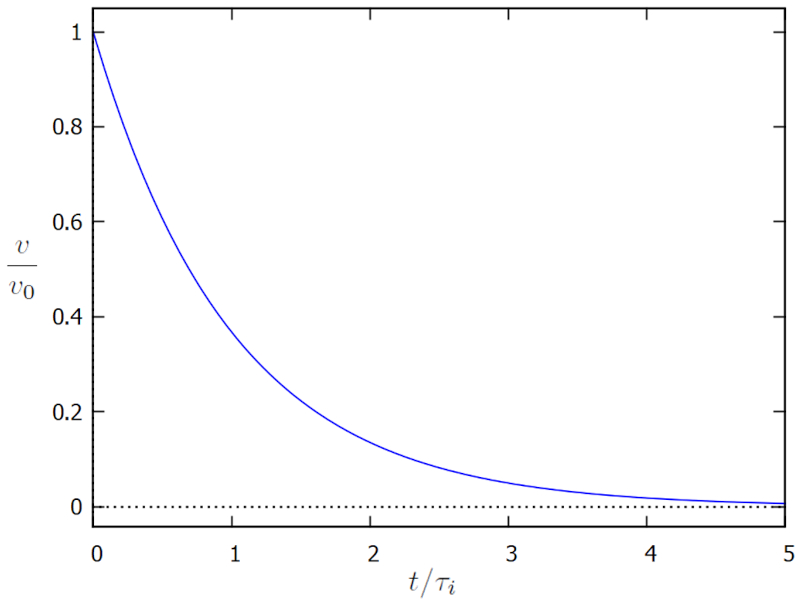
que se representa a continuaci n:

image

El gr fico ilustra c mo la viscosidad obliga al cuerpo a descender hasta cero, lo que ocurre aproximadamente en un tiempo del orden de la tiempo de viscosidad y masa inercial ($\tau_i$).

En el caso de un cuerpo cayendo en un medio viscoso, la ecuaci n de movimiento es una ecuaci n de la posición ($s$) en funci n de la velocidad inicial ($v_0$), la tiempo de viscosidad y masa inercial ($\tau_i$) y el tiempo ($t$):

equation=14501

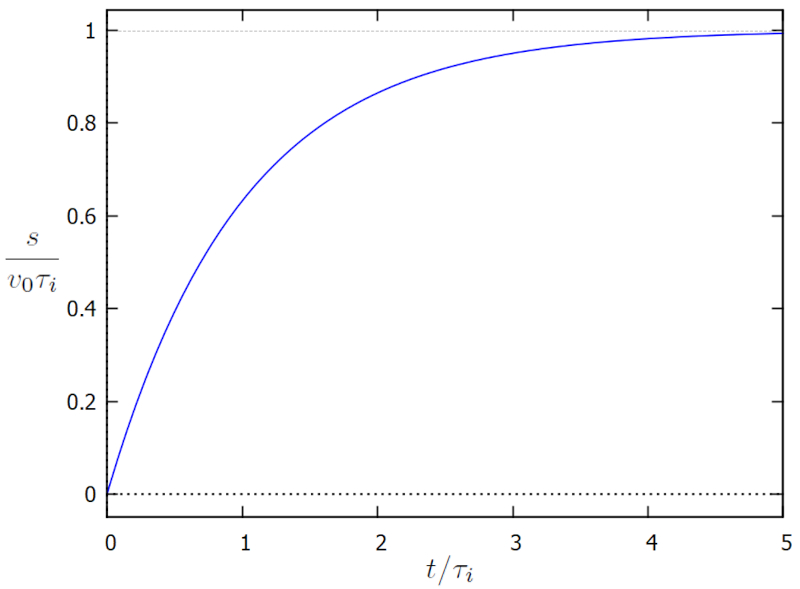
A partir desta equa o, obt m-se integrando com tempo inicial zero e una posición inicial ($s_0$):

equation=14502

que se representa a continuaci n:

image

model

La forma m s simple de la fuerza viscosa ($F_v$) es aquella que es proporcional a la velocidad ($v$) del cuerpo, representada por:

kyon

La constante de proporcionalidad, tambi n conocida como la constante de fuerza viscosa ($b$), depende en general de la forma del objeto y de la viscosidad del medio en el que se desplaza. Un ejemplo de este tipo de fuerza es la que ejerce una corriente sobre un cuerpo esf rico, cuya expresi n matem tica se conoce como la ley de Stokes.

En el caso en que la masa inercial ($m_i$) es igual a la masa inicial ($m_0$),

equation=12552

la derivada del momento ser igual a la masa multiplicada por la derivada de la velocidad ($v$). Dado que la derivada de la velocidad es la aceleración instantanea ($a$), obtenemos que la fuerza con masa constante ($F$) es igual a

kyon

En el caso de un cuerpo que cae en un medio viscoso, la fuerza total, la fuerza con masa constante ($F$), es igual a menos la fuerza viscosa ($F_v$), por lo tanto,

kyon

La fuerza total la fuerza con masa constante ($F$) es igual a menos la fuerza viscosa ($F_v$):

equation=15553

obtenemos la ecuaci n de movimiento para un cuerpo de la masa inercial ($m_i$) y la aceleración instantanea ($a$) de la siguiente forma:

kyon

Con la ecuaci n de movimiento de un cuerpo en un medio viscoso, tenemos la derivada de la velocidad ($v$) en el tiempo ($t$) con la constante de fuerza viscosa ($b$) y la aceleración gravitacional ($g$):

equation=14499

Lo que define la tiempo de viscosidad y masa inercial ($\tau_i$) como:

kyon

Al resolver la ecuaci n para la velocidad ($v$) en el tiempo ($t$) con la masa inercial ($m_i$) y la constante de fuerza viscosa ($b$):

equation=14499

Suponiendo que en un tiempo inicial nulo y con la velocidad inicial ($v_0$), obtenemos con la tiempo de viscosidad y masa inercial ($\tau_i$) la soluci n:

kyon

Si integramos la ecuaci n de la posición ($s$) en funci n de el tiempo ($t$) con la velocidad inicial ($v_0$) y la tiempo de viscosidad y masa inercial ($\tau_i$):

equation=14501

desde un tiempo inicial nulo hasta el tiempo ($t$), y desde una posición inicial ($s_0$) hasta la posición ($s$), obtenemos

kyon