User:


Cross Product or Vector Product
Storyboard

The so-called cross product or vector product allows to determine an orthogonal vector to the vectors that create it. Its magnitude corresponds to twice the area that would have a rectangle with sides equal to the magnitudes of each of the vectors.

>Model

ID:(1259, 0)


Graphical representation of the cross product
Definition

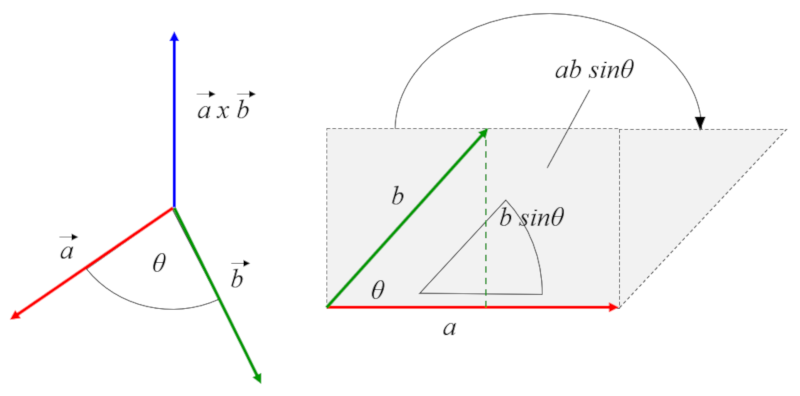
The cross product generates a vector that is orthogonal to those that generate it and whose magnitude is the multiplication of the magnitudes of each vector and the sine of the angle between them.

The length of the resulting vector corresponds to the area of the parallelepiped formed by the two vectors that generate it:

ID:(4582, 0)


Cross Product or Vector Product
Description

The so-called cross product or vector product allows to determine an orthogonal vector to the vectors that create it. Its magnitude corresponds to twice the area that would have a rectangle with sides equal to the magnitudes of each of the vectors.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$\theta$
theta
Angulo entre los vectores
rad
$\vec{a}$
&a
Component of the Vector $\vec{a}$ in $\hat{x}$
m
$\mid\vec{a}\mid$
a
Magnitud del vector
m
$\mid\vec{b}\mid$
b
Magnitud del vector
m
$\mid\vec{a}\times\vec{b}\mid$
axb
Product Cruz and Angle
-
$\vec{b}$
&b
Vector
m
$b_y$
b_y
Vector que resulta de la suma
m

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

Examples

The cross product generates a vector that is orthogonal to those that generate it and whose magnitude is the multiplication of the magnitudes of each vector and the sine of the angle between them.

The length of the resulting vector corresponds to the area of the parallelepiped formed by the two vectors that generate it:

(ID 4582)

El producto cruz se puede definir como una determinante de una matriz cuyas lineas son los versores del sistema \hat{n}=(e_x,e_y,e_z), en la segunda y tercera l neas las coordenadas de los vectores \vec{a}=(a_x,a_y,a_z) y \vec{b}=(b_x,b_y,b_z) por lo que se obtiene un vector

$ \vec{a}\times\vec{b} =( a_y b_z - a_z b_y , a_z b_x - a_x b_z , a_x b_y - a_y b_x )$

(ID 3676)

Si se expresa el producto cruz en funci n del versor \hat{e} ortogonal a los vectores \vec{a} y \vec{b} se tiene que

$ \mid\vec{a}\times\vec{b}\mid = \mid\vec{a}\mid \mid\vec{b}\mid \sin \theta $

donde \theta es el angulo entre ambos vectores.

(ID 3677)

ID:(1259, 0)