Utilizador:
Correntes paralelas
Descrição 
Quando permitimos que duas correntes fluam de forma paralela, observamos uma força atrativa entre os fios.
Vale lembrar que as correntes consistem em elétrons em movimento, e os elétrons naturalmente se repelem devido às suas cargas negativas. No entanto, quando essas cargas estão em movimento, essa força repulsiva se transforma em uma força atrativa, resultando na observação de atração entre os condutores carregados negativamente.
ID:(11772, 0)
Correntes paralelas opostas
Descrição
Quando permitimos que duas correntes fluam de forma paralela, mas em direções opostas, observamos uma força repulsiva entre os fios.
Comparando este experimento com aquele em que o fluxo é paralelo, mas flui na mesma direção, a diferença chave reside no fato de que, no último caso, existe uma velocidade relativa.
ID:(11773, 0)
Correntes paralelas, o campo não é elétrico
Descrição
Se uma placa metálica é colocada entre ambos os condutores, nenhum efeito notável é observado:
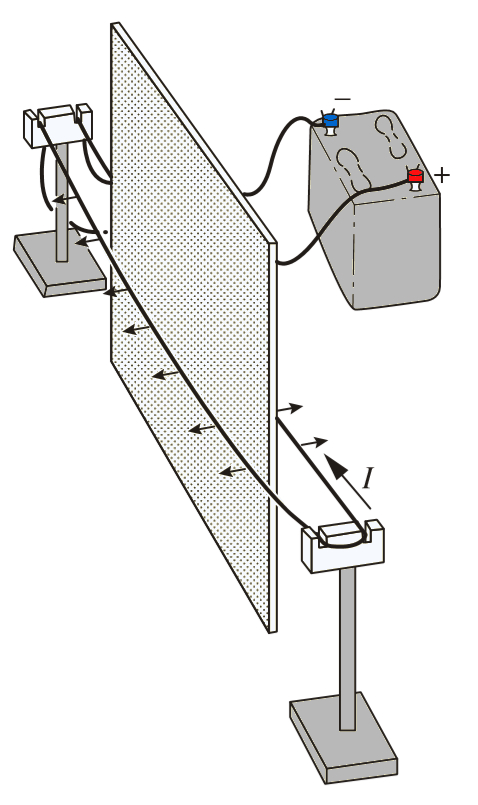
Portanto, concluímos que o campo gerado não corresponde a um campo elétrico tradicional.
ID:(11774, 0)
Efeito da corrente em uma bússola
Descrição
Quando uma bússola é exposta a uma corrente elétrica, as seguintes observações podem ser feitas:
Em resumo, a agulha da bússola: • não gira se não houver corrente elétrica presente • gira quando há um fluxo de corrente elétrica • se a direção do fluxo de corrente elétrica for invertida, a rotação da agulha também é invertida.
ID:(11775, 0)
Detecção do campo magnético gerado
Descrição
Quando exploramos o espaço ao redor de um fio com uma bússola, percebemos que a corrente elétrica induz a presença de um campo magnético:
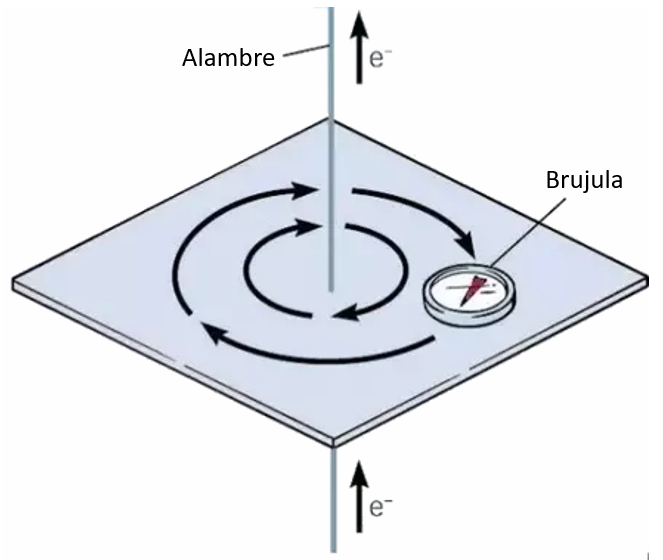
É por isso que fios paralelos podem se atrair ou se repelir dependendo da direção da corrente elétrica. A chave aqui é compreender que:
A corrente elétrica gera um campo magnético, e esse campo magnético exerce uma força sobre cargas em movimento.
ID:(11776, 0)
Dinâmica de Partículas
Descrição
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Exemplos
La força ($F$), que gera la densidade do fluxo magnético ($B$) sobre ERROR:54609, movendo-se sob um ângulo entre velocidade e campo magnético ($\theta$) com la velocidade ($v$), expresso como:
| $ F = q v B \sin \theta $ |
(ID 3873)
A equa o de movimento resulta do equil brio entre a for a gerada por la densidade do fluxo magnético ($B$) atuando sobre la carga ($q$) e la massa molar ($m$), que se desloca com la velocidade das partículas ($v$) em o rádio ($r$). Isso expresso pela seguinte rela o:
| $ m \displaystyle\frac{ v ^2}{ r }= q v B $ |
(ID 3229)
A rbita em um raio de giração da partícula no campo magnético ($r$) depende de la massa molar ($m$), la velocidade ($v$), la charge ($Q$) e la densidade do fluxo magnético ($B$), sendo descrita pela seguinte rela o:
| $ r =\displaystyle\frac{ m v }{ q B }$ |
(ID 3874)
La velocidade angular ($\omega$) derivado de la carga ($q$), la densidade do fluxo magnético ($B$) e la massa molar ($m$), utilizando a seguinte rela o:
| $ \omega =\displaystyle\frac{ q B }{ m }$ |
(ID 10058)
ID:(818, 0)