Usuario:


Inducción magnética
Storyboard

Una inductancia es un elemento que al variar la corriente que circula por el genera un potencial que se opone al mismo flujo de corriente. Opera como un sistema que amortigua la corriente que circula por el. Funciona mediante una bobina en que la corriente genera un campo magnético que a su vez genera el potencial que se opone a la corriente.

>Modelo

ID:(1392, 0)


Inducción magnética
Descripción

Una inductancia es un elemento que al variar la corriente que circula por el genera un potencial que se opone al mismo flujo de corriente. Opera como un sistema que amortigua la corriente que circula por el. Funciona mediante una bobina en que la corriente genera un campo magnético que a su vez genera el potencial que se opone a la corriente.

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$\vec{E}$
&E
Campo eléctrico
V/m
$B$
B
Densidad de flujo magnético
T
$\Delta\varphi$
Dphi
Diferencia de potencial
V
$ds$
ds
Distancia infinitesimal
m
$l$
l
Largo de la bobina
m
$\varphi$
phi
Potencial eléctrico
V
$\varphi_0$
phi_0
Potencial eléctrico base
V
$v$
v
Velocidad
m/s

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

La diferencia de potencial ($\Delta\varphi$) es igual a la suma de el campo eléctrico ($\vec{E}$) a lo largo de un camino integrado sobre el elemento de camino recorrido ($d\vec{s}$):

$ \Delta\varphi = -\displaystyle\int_C \vec{E}\cdot d\vec{s} $



Como la diferencia de potencial ($\Delta\varphi$) se calcula considerando el potencial eléctrico ($\varphi$) menos el potencial eléctrico base ($\varphi_0$):

$ \Delta\varphi = \varphi - \varphi_0 $



por lo que

$ \varphi =\varphi_0 - \displaystyle\int_C \vec{E}\cdot d\vec{s}$

(ID 3844)

Ejemplos

El potencial eléctrico ($\varphi$) se puede calcular de el potencial eléctrico base ($\varphi_0$) y el campo eléctrico ($\vec{E}$) integrado a lo largo de un camino sobre el elemento de camino recorrido ($d\vec{s}$):

$ \varphi =\varphi_0 - \displaystyle\int_C \vec{E}\cdot d\vec{s}$

(ID 3844)

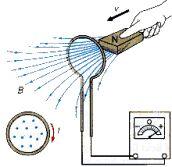
Si se desplaza el conductor a trav s de un campo magn tico \vec{B} o el campo magn tico respecto del conductor con una velocidad \vec{v} se genera una fuerza seg n la Ley de Lorentz igual a

$ F = q v B \sin \theta $



donde se asumi que la carga es q y la velocidad es ortogonal al campo magn tico.

La fuerza se puede describir por un campo el ctrico inducido \vec{E} y este se puede asociar a una diferencia de potencial \Delta V dividido por el largo del l del conductor

F=qE=q\displaystyle\frac{\Delta V}{l}

Con ello el potencial inducido es igual a

$ \Delta V = l v B $

(ID 3220)

ID:(1392, 0)