Parallele hydraulische Elemente
Storyboard 
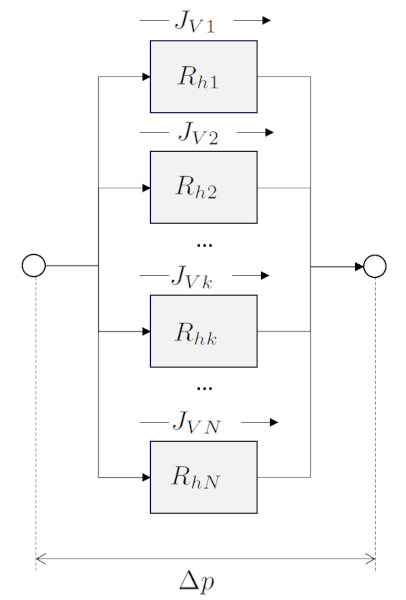
Wenn hydraulische Elemente parallel geschaltet sind, wird der Durchfluss zwischen ihnen verteilt, während der Druckabfall für alle gleich ist. Die Summe der individuellen Durchflüsse ergibt den Gesamtdurchfluss, und daher entspricht der Gesamthydraulikwiderstand dem Kehrwert der Summe der Kehrwerte der individuellen Hydraulikwiderstände. Andererseits werden hydraulische Leitfähigkeiten direkt addiert.
ID:(1467, 0)
Parallele hydraulische Elemente
Storyboard 
Wenn hydraulische Elemente parallel geschaltet sind, wird der Durchfluss zwischen ihnen verteilt, während der Druckabfall für alle gleich ist. Die Summe der individuellen Durchflüsse ergibt den Gesamtdurchfluss, und daher entspricht der Gesamthydraulikwiderstand dem Kehrwert der Summe der Kehrwerte der individuellen Hydraulikwiderstände. Andererseits werden hydraulische Leitfähigkeiten direkt addiert.
Variablen
Berechnungen
Berechnungen
Gleichungen
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
Weiterhin, unter Verwendung der Beziehung f r die Hydraulic Resistance ($R_h$):
ergibt sich:
Der Volumenstrom ($J_V$) kann aus die Hydraulische Leitfähigkeit ($G_h$) und die Druckunterschied ($\Delta p$) unter Verwendung der folgenden Gleichung berechnet werden:
Weiterhin, unter Verwendung der Beziehung f r die Hydraulic Resistance ($R_h$):
ergibt sich:
Die Parallele hydraulische Gesamtleitfähigkeit ($G_{pt}$) in Kombination mit die Hydraulische Leitfähigkeit in einem Netzwerk ($G_{hk}$) in
und zusammen mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) und der Gleichung
f hrt zu die Insgesamt hydraulischen Widerstand in Parallel ($R_{pt}$) ber
Da die Hydraulic Resistance ($R_h$) gem der folgenden Gleichung gleich die Hydraulische Leitfähigkeit ($G_h$) ist:
und da die Hydraulische Leitfähigkeit ($G_h$) wie folgt in Bezug auf die Viskosität ($\eta$), der Rohrradius ($R$) und der Rohrlänge ($\Delta L$) ausgedr ckt wird:
k nnen wir folgern, dass:
Mit der Gesamtfluss ($J_{Vt}$), das gleich der Volumenstrom in einem Netzwerk ($J_{Vk}$) ist:
und mit die Druckunterschied ($\Delta p$) und die Hydraulische Leitfähigkeit in einem Netzwerk ($G_{hk}$), zusammen mit der Gleichung
f r jedes Element, gelangen wir zu dem Schluss, dass mit die Parallele hydraulische Gesamtleitfähigkeit ($G_{pt}$):
$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$
wir haben
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns erm glicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
k nnen wir die Hydraulische Leitfähigkeit ($G_h$) einf hren, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
um zu folgendem Ergebnis zu gelangen:
Wenn wir das Hagen-Poiseuille-Gesetz betrachten, das es uns erm glicht, der Volumenstrom ($J_V$) aus der Rohrradius ($R$), die Viskosität ($\eta$), der Rohrlänge ($\Delta L$) und die Druckunterschied ($\Delta p$) zu berechnen:
k nnen wir die Hydraulische Leitfähigkeit ($G_h$) einf hren, das in Bezug auf der Rohrlänge ($\Delta L$), der Rohrradius ($R$) und die Viskosität ($\eta$) definiert ist:
um zu folgendem Ergebnis zu gelangen:
Beispiele
Eine effiziente Methode, ein Rohr mit variablen Querschnitten zu modellieren, besteht darin, es in Abschnitte mit konstantem Radius zu unterteilen und dann die hydraulischen Widerst nde in Reihe zu summieren. Nehmen wir an, wir haben eine Serie von Elementen die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$), deren Widerstand von die Viskosität ($\eta$), der Zylinder k Radio ($R_k$) und der Länge des Rohrs k ($\Delta L_k$) abh ngt, gem der folgenden Gleichung:
In jedem Element betrachten wir eine Druckunterschied in einem Netzwerk ($\Delta p_k$) zusammen mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) und dem Volumenstrom der Volumenstrom ($J_V$), wobei das Darcy-Gesetz angewendet wird:
Der Gesamtwiderstand des Systems, der Flujo de Volumen Total ($J_{Vt}$), ist die Summe der individuellen hydraulischen Widerst nde ERROR:10133,0 jedes Abschnitts:
Daher ergibt sich:
$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$
Somit kann das System als ein einzelnes Rohr mit einem Gesamtwiderstand modelliert werden, der durch die Summe der einzelnen Komponenten berechnet wird:
Im Fall einer Summe, bei der die Elemente in Serie geschaltet sind, wird die Gesamthydraulikleitf higkeit des Systems berechnet, indem die individuellen hydraulischen Leitf higkeiten jedes Elements addiert werden.
die Insgesamt hydraulischen Widerstand in Parallel ($R_{pt}$), zusammen mit die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$), in
und zusammen mit die Hydraulische Leitfähigkeit in einem Netzwerk ($G_{hk}$) und der Gleichung
f hrt zu die Parallele hydraulische Gesamtleitfähigkeit ($G_{pt}$) kann berechnet werden mit:
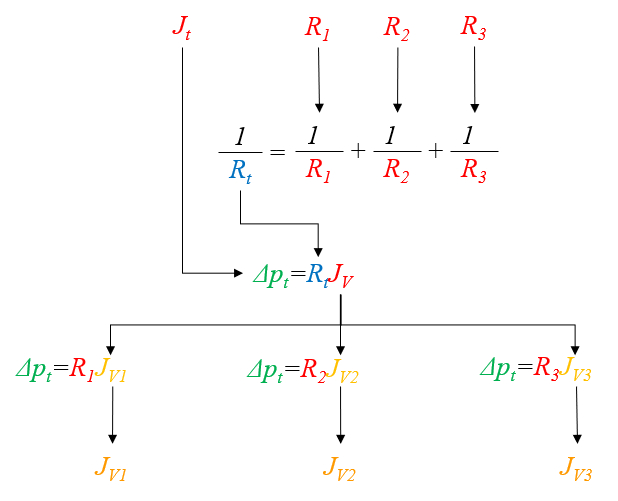
Zuerst werden die Werte f r die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) unter Verwendung der Variablen die Viskosität ($\eta$), der Zylinder k Radio ($R_k$) und der Länge des Rohrs k ($\Delta L_k$) durch die folgende Gleichung berechnet:
Diese Werte werden dann summiert, um die Insgesamt hydraulischen Widerstand in Serie ($R_{st}$) zu erhalten:
Mit diesem Ergebnis kann die Variación de la Presión ($\Delta p$) f r die Insgesamt hydraulischen Widerstand in Parallel ($R_{pt}$) berechnet werden, indem man folgende Gleichung verwendet:
Sobald die Variación de la Presión ($\Delta p$) ermittelt ist, wird der Volumenstrom in einem Netzwerk ($J_{Vk}$) wie folgt berechnet:
F r den Fall von drei Widerst nden k nnen die Berechnungen in der folgenden Grafik visualisiert werden:
Durch die Einf hrung von die Hydraulische Leitfähigkeit ($G_h$) k nnen wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
Durch die Einf hrung von die Hydraulische Leitfähigkeit ($G_h$) k nnen wir die Hagen-Poiseuille-Gleichung mit die Druckunterschied ($\Delta p$) und der Volumenstrom ($J_V$) mithilfe der folgenden Gleichung umschreiben:
Mit der Rohrradius ($R$), die Viskosität ($\eta$) und der Rohrlänge ($\Delta L$) haben wir, dass eine Hydraulische Leitfähigkeit ($G_h$) ist:
Die Summe der Bodenschichten in Parallele, dargestellt als der Gesamtfluss ($J_{Vt}$), entspricht der Summe von der Volumenstrom in einem Netzwerk ($J_{Vk}$):
Die Parallele hydraulische Gesamtleitfähigkeit ($G_{pt}$) wird mit der Summe von die Hydraulische Leitfähigkeit in einem Netzwerk ($G_{hk}$) berechnet:
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitf higkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) w re, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
Im Zusammenhang mit dem elektrischen Widerstand gibt es dessen Inverses, das als elektrische Leitf higkeit bekannt ist. Ebenso kann das, was die Hydraulische Leitfähigkeit ($G_h$) w re, in Bezug auf die Hydraulic Resistance ($R_h$) durch den Ausdruck definiert werden:
Da die Hydraulic Resistance ($R_h$) dem Kehrwert von die Hydraulische Leitfähigkeit ($G_h$) entspricht, kann es aus dem Ausdruck des letzteren berechnet werden. Auf diese Weise k nnen wir Parameter identifizieren, die mit der Geometrie (der Rohrlänge ($\Delta L$) und der Rohrradius ($R$)) und der Art des Fluids (die Viskosität ($\eta$)) zusammenh ngen und die gemeinsam als eine Hydraulic Resistance ($R_h$) bezeichnet werden k nnen:
Die Insgesamt hydraulischen Widerstand in Parallel ($R_{pt}$) kann als Kehrwert der Summe von die Hydraulischer Widerstand in einem Netzwerk ($R_{hk}$) berechnet werden:
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
Darcy schreibt die Hagen-Poiseuille-Gleichung so um, dass die Druckunterschied ($\Delta p$) gleich die Hydraulic Resistance ($R_h$) mal der Volumenstrom ($J_V$) ist:
ID:(1467, 0)