Utilizador:
Mecanismos de transporte de calor
Storyboard 
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Uma vez que la calor transportado ($dQ$) uma fun o de o comprimento do conductor ($L$), la seção ($S$), la variação de tempo ($dt$), la diferença de temperatura no condutor ($\Delta T_0$) e la condutividade térmica ($\lambda$), de acordo com a seguinte equa o:
Com a equa o para la taxa de fluxo de calor ($q$) definida como:
No caso infinitesimal, onde o comprimento do conductor ($L$) se reduz a uma distância percorrida ($dz$) e la diferença de temperatura no condutor ($\Delta T_0$) se torna la variação de temperatura ($dT$), a equa o se simplifica para:
A quantidade de la calor transportado ($dQ$) atrav s de uma distância percorrida ($dz$) pode ser calculada usando la taxa de fluxo de calor ($q$) e la variação de tempo ($dt$) com la seção ($S$) atrav s da seguinte equa o:
$dQ = -\displaystyle\frac{\partial}{\partial z}(q S dt) dz$
Uma vez que la taxa de fluxo de calor ($q$) com la variação de temperatura ($dT$) e la condutividade térmica ($\lambda$) definido como:
Portanto,
$dQ = \displaystyle\frac{\partial}{\partial z}(\lambda \displaystyle\frac{\partial T}{\partial z}) S dz dt$
Por outro lado, podemos relacionar la calor fornecido ao líquido ou sólido ($\Delta Q$) com la massa ($M$), o calor específico ($c$) e la variação de temperatura ($\Delta T$) atrav s da seguinte equa o:
Neste caso, com la variação de volume ($\Delta V$), a equa o se torna:
$dQ=\rho dV c dT = \rho c S dz dT$
E finalmente, obtemos:
Exemplos
No caso de um s lido e de maneira semelhante para um l quido, podemos descrever o sistema como uma estrutura de tomos ligados por algo que se comporta como uma mola. Quando ambas as extremidades t m temperaturas de uma diferença de temperatura no condutor ($\Delta T_0$), com la temperatura da superfície interna ($T_{is}$) e la temperatura da superfície externa ($T_{es}$):
A diferen a de temperatura implica que os tomos nas extremidades oscilam de forma diferente; os tomos na zona de alta temperatura ter o uma amplitude maior em suas oscila es em compara o com os tomos na zona de baixa temperatura.
No entanto, essa diferen a gradualmente levar toda a cadeia a oscilar de tal forma que, no final, a amplitude variar ao longo do caminho, desde os valores mais altos onde a temperatura tamb m maior, at os valores mais baixos na zona de menor temperatura.
Dessa forma, la diferença de temperatura no condutor ($\Delta T_0$) leva a uma calor transportado ($dQ$) em uma variação de tempo ($dt$).
Para entender como o calor conduzido, voc pode imaginar que um corpo pode ser representado por cadeias de molas que oscilam de acordo com sua temperatura. Se em uma extremidade do corpo a temperatura for mais alta, a oscila o correspondente tamb m ser maior. medida que nos afastamos dessa extremidade, as molas vizinhas oscilam com menor amplitude, resultando na distribui o gradual da oscila o/temperatura ao longo da cadeia, como ilustrado abaixo:
A capacidade de condu o de calor ser maior quando houver mais cadeias ( rea transversal) presentes e ser mais lenta medida que as cadeias se tornarem mais longas.
Os modelos de transfer ncia e condu o de calor sugerem que poss vel desenvolver uma rela o que incorpore os tr s mecanismos juntos. Esta equa o deve levar em considera o la calor transportado ($dQ$), la variação de tempo ($dt$), la diferença de temperatura ($\Delta T$), la seção ($S$) e o coeficiente de transporte total (médio múltiplo, duas interfaces) ($k$):
Matematicamente, isso pode ser expresso da seguinte forma:
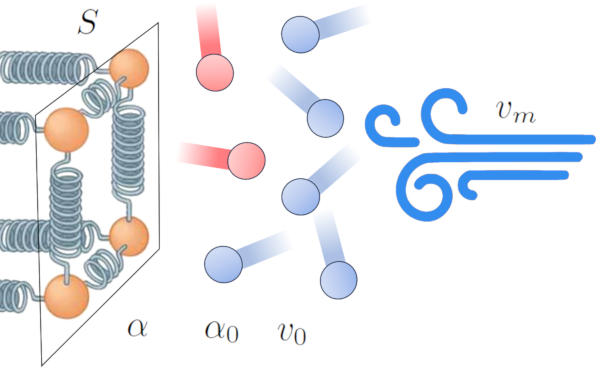
Um dos efeitos da transfer ncia de calor de um condutor para um meio externo o aquecimento do meio pr ximo interface, criando uma zona de interfer ncia na transmiss o. Isso diminui a efici ncia da transfer ncia e tende a formar uma camada isolante que reduz o fluxo de energia.
No entanto, esse efeito pode mudar na presen a de vento. O vento pode remover a camada de tomos e mol culas em alta temperatura, aumentando a efici ncia da transfer ncia de calor. Isso indica que o coeficiente de transmissão ($\alpha$) influenciado por la velocidade média ($v_m$) [1,2]:
Nesse contexto, modelamos a rela o com base em ERROR:9844,0 e um fator de refer ncia de o velocidade de referência de mídia ($v_0$).
A rela o matem tica que descreve esse fen meno para um g s com o coeficiente de transmissão em gases, dependente da velocidade ($\alpha_{gv}$), la velocidade média ($v_m$), o coeficiente de transmissão em gases, independente da velocidade ($\alpha_{g0}$) e o coeficiente de transmissão fator de velocidade do gás ($v_{g0}$) :
E para um l quido com o coeficiente de transmissão em líquido, dependente da velocidade ($\alpha_{wv}$), la velocidade média ($v_m$), o coeficiente de transmissão em líquido, independente da velocidade ($\alpha_{w0}$) e o coeficiente de transmissão fator de velocidade do líquido ($v_{w0}$):
Isso demonstra como o vento pode influenciar significativamente a efici ncia da transfer ncia de calor entre um condutor e um meio externo.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sobre o Movimento de Fluidos com Muito Pouca Fric o), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (A Depend ncia do Coeficiente de Transfer ncia de Calor com o Comprimento da Tubula o), Wilhelm Nusselt, 1910
Para um condutor com valores de o comprimento do conductor ($L$) e la seção ($S$), o fluxo de la calor transportado ($dQ$) descrito sob la variação de tempo ($dt$) e la condutividade térmica ($\lambda$) da seguinte forma:
No caso infinitesimal, onde o comprimento do conductor ($L$) se reduz a uma distância percorrida ($dz$) e la diferença de temperatura no condutor ($\Delta T_0$) se torna la variação de temperatura ($dT$), a equa o para la taxa de fluxo de calor ($q$) se simplifica para:
[1] "Th orie analytique de la chaleur" (A Teoria Anal tica do Calor), Joseph Fourier, Cambridge University Press (2009) (original de 1822)
La taxa de fluxo de calor ($q$) definido em termos de la calor transportado ($dQ$), la variação de tempo ($dt$) e la seção ($S$) da seguinte forma:
A defini o de la taxa de fluxo de calor ($q$) estabelecida utilizando la condutividade térmica ($\lambda$) e la variação de temperatura ($dT$) como fun o de la distância percorrida ($dz$) atrav s da seguinte equa o:
Ao estudar o fluxo de calor, obtemos a equa o para la temperatura absoluta ($T$) como fun o de la posição ao longo de um eixo ($z$), o tempo ($t$) e la condutividade térmica ($\lambda$), que se torna o calor específico ($c$). A equa o para la densidade ($\rho$) se simplifica para:
ID:(1512, 0)
