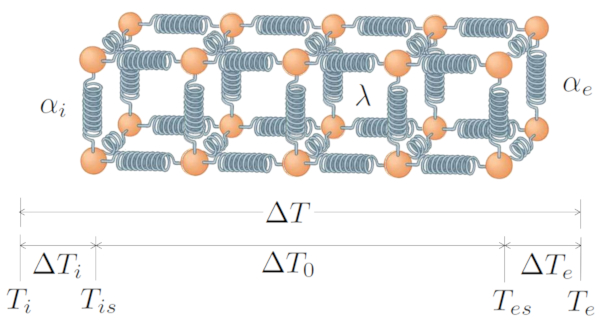Utilisateur:
Transfert de chaleur
Storyboard 
La chaleur est conduite à l'intérieur d'un milieu jusqu'à l'interface avec un autre milieu. Entre les deux, la chaleur est transférée en fonction de la différence de température entre les milieux, de la surface de contact et d'une constante de transfert thermique. Lorsque l'un des milieux est un gaz (par exemple, l'air) ou un liquide (par exemple, l'eau), la constante de transfert thermique dépend de la structure de l'interface et de la vitesse de déplacement du milieu gazeux ou liquide.
ID:(776, 0)
Transfert de chaleur
Storyboard
La chaleur est conduite à l'intérieur d'un milieu jusqu'à l'interface avec un autre milieu. Entre les deux, la chaleur est transférée en fonction de la différence de température entre les milieux, de la surface de contact et d'une constante de transfert thermique. Lorsque l'un des milieux est un gaz (par exemple, l'air) ou un liquide (par exemple, l'eau), la constante de transfert thermique dépend de la structure de l'interface et de la vitesse de déplacement du milieu gazeux ou liquide.
Variables
Calculs
à 
,
puis, sélectionnez la variable: 
à 
Calculs
Variable
Donnée
Calculer
Cible :
Équation
À utiliser
Équations
Exemples
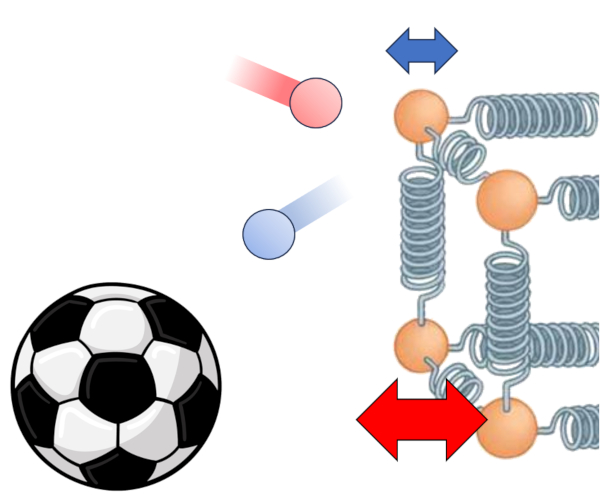
Consid rez un volume dans lequel des particules rebondissent contre les parois une vitesse repr sentant leur temp rature. Chaque fois qu'elles frappent une grille centrale, elles entrent en collision avec les atomes dun solide, les for ant osciller. Cette oscillation se propage travers le solide jusqu' l'autre extr mit , o l' nergie est transmise au gaz par de nouvelles collisions.
Exp rimentation :
Il est possible de modifier la vitesse des particules dans les bo tes lat rales et dobserver comment l nergie est transf r e au solide, puis au gaz du c t oppos .
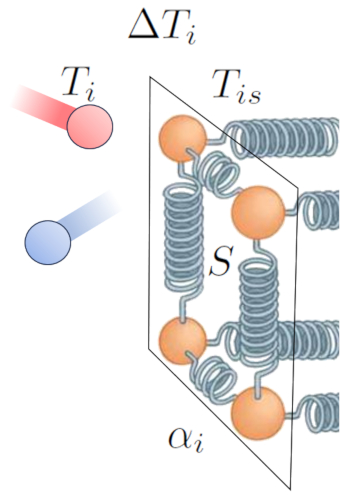
Le principal moteur du transfert de chaleur d'un milieu un conducteur est la diff rence de temp rature. Dans le milieu a température intérieure ($T_i$), les particules ont plus d' nergie, et lorsqu'elles entrent en collision avec celles du conducteur une température de la surface intérieure ($T_{is}$), elles ont tendance augmenter l' nergie de ce dernier. Cette interaction peut tre repr sent e comme suit :
Au-del de la temp rature en elle-m me, le flux de chaleur d pend de a différence de température à l'interface interne ($\Delta T_i$) :
Un autre facteur cl est le nombre d'atomes dont l'amplitude d'oscillation peut tre augment e, ce qui d pend de a section ($S$). Enfin, nous devons galement prendre en compte les propri t s de surface, d crites par le coefficient de transmission interne ($\alpha_i$), qui correspondent la relation entre la chaleur transmise, la surface, la diff rence de temp rature et le temps coul :
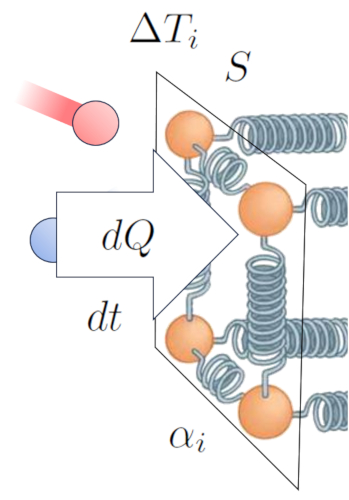
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface interne ($\Delta T_i$) et le coefficient de transmission interne ($\alpha_i$) :
Cela peut s'exprimer math matiquement comme suit :
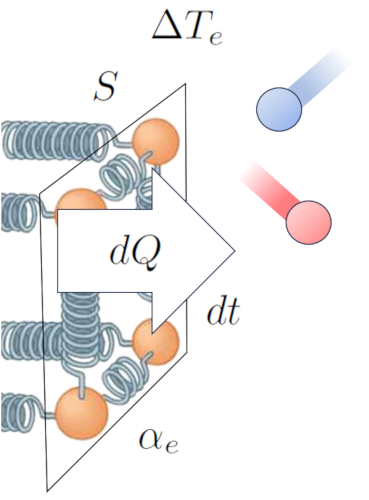
Le principal moteur du transfert de chaleur d'un conducteur un milieu est la diff rence de temp rature. Lorsque a température de la surface extérieure ($T_{es}$), les particules ont plus d' nergie et oscillent avec une amplitude plus grande en interagissant avec les atomes et les mol cules du milieu une température extérieure ($T_e$). Cela a tendance augmenter l' nergie de ces derniers. Cette interaction peut tre repr sent e comme suit :
Au-del de la temp rature, le flux de chaleur d pend de a différence de température à l'interface externe ($\Delta T_e$).
Un autre facteur cl est le nombre d'atomes qui peuvent avoir leur amplitude d'oscillation augment e, ce qui d pend de a section ($S$). Enfin, nous devons galement tenir compte des propri t s de surface, repr sent es par le coefficient de transmission externe ($\alpha_e$), qui correspondent la relation entre la chaleur transf r e, la surface, la diff rence de temp rature et le temps coul :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface externe ($\Delta T_e$) et le coefficient de transmission externe ($\alpha_e$) :
Cela peut tre exprim math matiquement comme suit :
La premi re description du mod le de transfert de chaleur l'interface entre deux milieux a t d velopp e par Thomas Graham Balfour [1]. Sa th orie suppose que le taux de chaleur transmis d pend de la diff rence de temp rature et d'une constante propre l'interface.
Lorsque la chaleur est transf r e au conducteur, repr sent par a débit de chaleur ($q$) avec le coefficient de transmission interne ($\alpha_i$) et a différence de température à l'interface interne ($\Delta T_i$), la relation est exprim e par l' quation suivante :
Dans le cas o la chaleur passe du conducteur, identifi par a débit de chaleur ($q$) avec le coefficient de transmission externe ($\alpha_e$) et a différence de température à l'interface externe ($\Delta T_e$), la relation est sp cifi e comme suit :
[1] "The Theory of Heat" (La th orie de la chaleur), Thomas Graham Balfour, 1876.
Le syst me de base comprend un transfert g n r par a différence de température ($\Delta T$), qui se compose de a différence de température à l'interface interne ($\Delta T_i$), a différence de température dans le conducteur ($\Delta T_0$) et a différence de température à l'interface externe ($\Delta T_e$). Par cons quent :
Avec a débit de chaleur ($q$) responsable du transfert entre l'int rieur et le conducteur, utilisant le coefficient de transmission interne ($\alpha_i$) :
La conduction implique a conductivité thermique ($\lambda$) et le longueur du pilote ($L$) :
Et le transfert du conducteur vers l'ext rieur, avec le coefficient de transmission externe ($\alpha_e$), est repr sent par :
Tout cela est repr sent graphiquement par :
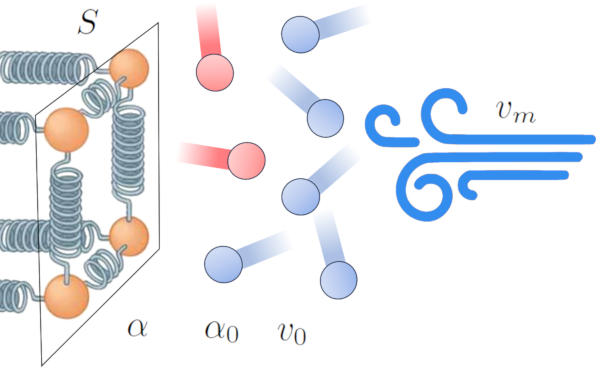
L'un des effets du transfert de chaleur d'un conducteur un milieu externe est le r chauffement du milieu pr s de l'interface, cr ant une zone d'interf rence dans la transmission. Cela diminue l'efficacit du transfert et tend former une couche isolante qui r duit le flux d' nergie.
Cependant, cet effet peut changer en pr sence de vent. Le vent peut liminer la couche d'atomes et de mol cules haute temp rature, am liorant ainsi l'efficacit du transfert de chaleur. Cela sugg re que le coefficient de transmission ($\alpha$) est influenc par a vitesse moyenne ($v_m$) [1,2] :
Dans ce contexte, nous mod lisons la relation en fonction de ERROR:9844,0 et d'un facteur de r f rence de le vitesse de référence du support ($v_0$).
La relation math matique qui d crit ce ph nom ne pour un gaz avec le coefficient de transmission dans les gaz, en fonction de la vitesse ($\alpha_{gv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans les gaz, indépendant de la vitesse ($\alpha_{g0}$) et le coefficient de transmission Facteur de vitesse du gaz ($v_{g0}$) est :
Et pour un liquide avec le coefficient de transmission dans le liquide, en fonction de la vitesse ($\alpha_{wv}$), a vitesse moyenne ($v_m$), le coefficient de transmission dans le liquide, indépendant de la vitesse ($\alpha_{w0}$) et le coefficient de transmission Facteur de vitesse du liquide ($v_{w0}$) :
Cela illustre comment le vent peut influencer de mani re significative l'efficacit du transfert de chaleur entre un conducteur et un milieu externe.
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sur le mouvement des fluides avec tr s peu de friction), Ludwig Prandtl, 1904
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (La d pendance du coefficient de transfert de chaleur la longueur du tuyau), Wilhelm Nusselt, 1910
A différence de température à l'interface interne ($\Delta T_i$) est calcul en soustrayant a température de la surface intérieure ($T_{is}$) de a température intérieure ($T_i$) :
A différence de température à l'interface externe ($\Delta T_e$) est calcul en soustrayant a température de la surface extérieure ($T_{es}$) de a température extérieure ($T_e$) :
Dans le cas d'un solide, et de mani re similaire pour un liquide, nous pouvons d crire le syst me comme une structure d'atomes li s par quelque chose qui se comporte comme un ressort. Lorsque les deux extr mit s ont des temp ratures de une différence de température dans le conducteur ($\Delta T_0$), avec a température de la surface intérieure ($T_{is}$) et a température de la surface extérieure ($T_{es}$) :
Dans le processus de transfert de chaleur, la temp rature diminue progressivement du syst me ayant la plus haute temp rature (interne) vers celui ayant la plus basse temp rature (externe). Dans ce processus, elle diminue d'abord de la temp rature moyenne interne a différence de température à l'interface interne ($\Delta T_i$), puis a différence de température dans le conducteur ($\Delta T_0$), et enfin a différence de température à l'interface externe ($\Delta T_e$). La somme de ces trois variations quivaut la chute totale, c'est- -dire a différence de température ($\Delta T$), comme illustr ci-dessous :
Le a débit de chaleur ($q$) est d fini en fonction du passage de a chaleur transportée ($dQ$) par a section ($S$) dans a variation temporelle ($dt$)xa0:
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface interne ($\Delta T_i$) et le coefficient de transmission interne ($\alpha_i$) :
De cette mani re, nous tablissons une relation qui nous permet de calculer a débit de chaleur ($q$) en fonction de a différence de température à l'interface externe ($\Delta T_e$) et le coefficient de transmission externe ($\alpha_e$) :
Le flux de chaleur ($q$) est une fonction de a conductivité thermique ($\lambda$), le longueur du pilote ($L$) et a différence de température dans le conducteur ($\Delta T_0$)xa0:
Si un milieu se d place avec une constante de le coefficient de transmission dans le liquide, en fonction de la vitesse ($\alpha_{wv}$), et que a vitesse moyenne ($v_m$) est gal
o le coefficient de transmission dans le liquide, indépendant de la vitesse ($\alpha_{w0}$) repr sente le cas o le milieu ne se d place pas, et le coefficient de transmission Facteur de vitesse du liquide ($v_{w0}$) est la vitesse de r f rence.
La constante de transfert thermique du mat riau pour le cas d'un liquide au repos est gale $340 J/m^2sK$, tandis que la vitesse de r f rence est de $0,0278 m/s$.
Dans le cas o un milieu se d place avec une constante de ERROR:5250.1 et que le coefficient de transmission dans les gaz, en fonction de la vitesse ($\alpha_{gv}$) est gal
o le coefficient de transmission dans les gaz, indépendant de la vitesse ($\alpha_{g0}$) repr sente le sc nario o le milieu ne se d place pas, et le coefficient de transmission Facteur de vitesse du gaz ($v_{g0}$) est la vitesse de r f rence.
La constante de transfert thermique pour le mat riau dans le cas d'un gaz au repos est de $5.6 J/m^2sK$, tandis que la vitesse de r f rence est de $1.41 m/s$.
ID:(776, 0)
