Position in einer Dimension
Storyboard 
Um die Position eines Objekts zu bestimmen, wird ein Koordinatensystem eingeführt, das es ermöglicht, einen Ursprungspunkt festzulegen und die Position durch die Messung der Entfernung entlang einer geraden Linie oder einer Kurve zu definieren. Demzufolge entspricht die Einheit der Position einer Längenmessung, wie Kilometer, Meter, Zentimeter und so weiter.Die Wahl des Koordinatensystems ist flexibel und erfolgt, um die Modellierung und die zugehörigen Berechnungen so weit wie möglich zu vereinfachen. Zum Beispiel, wenn sich das Objekt entlang einer Strecke bewegt, die nicht unbedingt gerade verläuft, ist es vorteilhaft, das Koordinatensystem entlang dieser Strecke zu definieren. In diesem speziellen Fall wird die Position als die Entfernung vom Ursprung oder dem Startpunkt der Strecke definiert.
ID:(607, 0)
Position, eine Dimension
Simulation 
Einer der grundlegenden Aspekte der Physik besteht darin, die Position der betrachteten Objekte zu bestimmen. Mit diesem Simulator lässt sich dieses Konzept erforschen: Man erzeugt einen roten Balken und verschiebt die Maus, um dessen Länge zu bestimmen. Diese Länge entspricht der Position des rechten Randes relativ zu einem Ursprung am linken Rand.
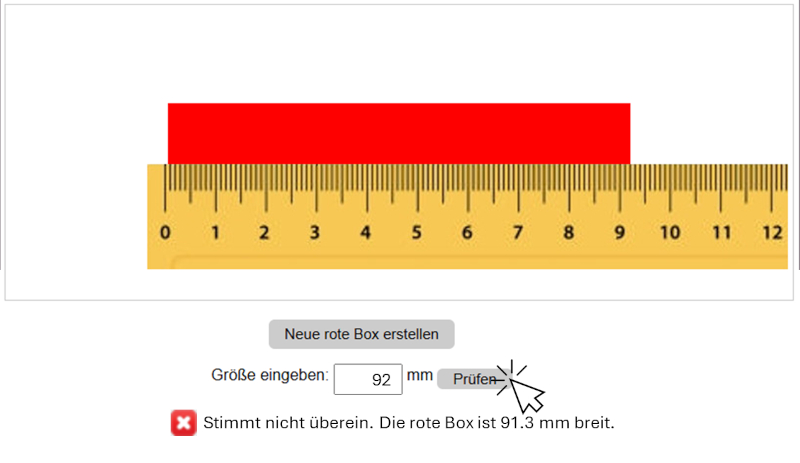
Messung der Größe der roten Box
Erstelle eine rote Box, indem du auf den Button unter dem Lineal klickst. Ziehe sie dann bei gedrückter linker Maustaste, bis die Null mit dem linken Rand der Box übereinstimmt. Lies den Wert am rechten Rand ab, gib ihn unten ein und klicke auf den Button, um zu überprüfen, ob die Messung korrekt ist.Betrachten Sie das Bedienfeld des Simulators:
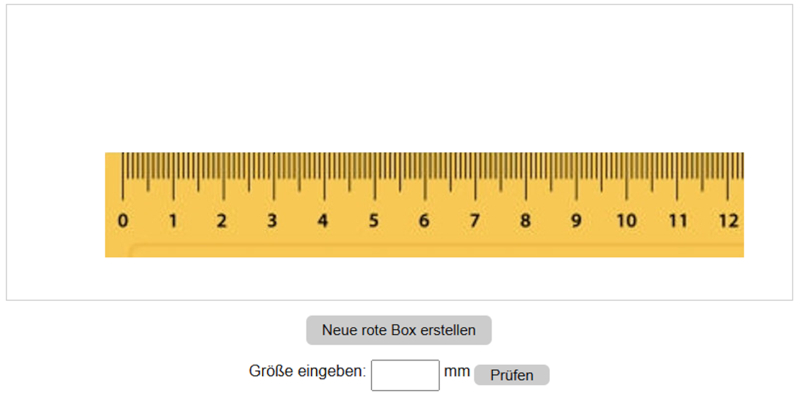
Erstellen Sie eine rote Box, indem Sie den Button unter dem Lineal drücken.
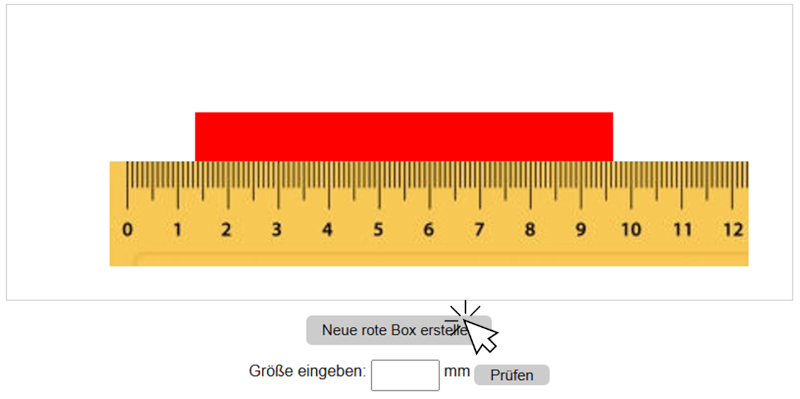
Ziehen Sie sie anschließend bei gedrückter linker Maustaste.
Achten Sie darauf, dass sie korrekt mit der Nullmarkierung am linken Rand der Box ausgerichtet ist.

Lesen Sie den Wert am rechten Rand ab.

Geben Sie den geschätzten Wert in das untere Feld ein (auch Dezimalwerte sind erlaubt).
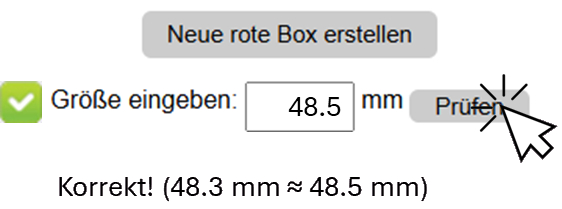
Wenn der Wert korrekt ist, wird dies bestätigt. Ist er falsch, wird der richtige Wert angezeigt.

Sie können experimentieren, indem Sie den Ursprung nach links verschieben und beobachten, wie schon eine kleine Fehljustierung zu einem abweichenden Ergebnis führt. Auch der eingegebene Wert kann angepasst werden er gilt als korrekt, solange er sich innerhalb einer Toleranz von einem Millimeter befindet.
Wenn uns jemand sagt, dass sich sein Standort 45km entfernt befindet, stellt sich sofort die Frage: Von wo aus? Das heißt, wir müssen den Ursprung kennen, der dieser Angabe Bedeutung verleiht.
Im Simulator bedeutet das, dass wir die Null der Messskala am linken Rand der roten Box platzieren müssen, um die Position des rechten Rands korrekt zu bestimmen.

Wird dies nicht sorgfältig gemacht, ist der an der rechten Seite abgelesene Wert falsch, und die Simulation zeigt uns, dass wir falsch gemessen haben:
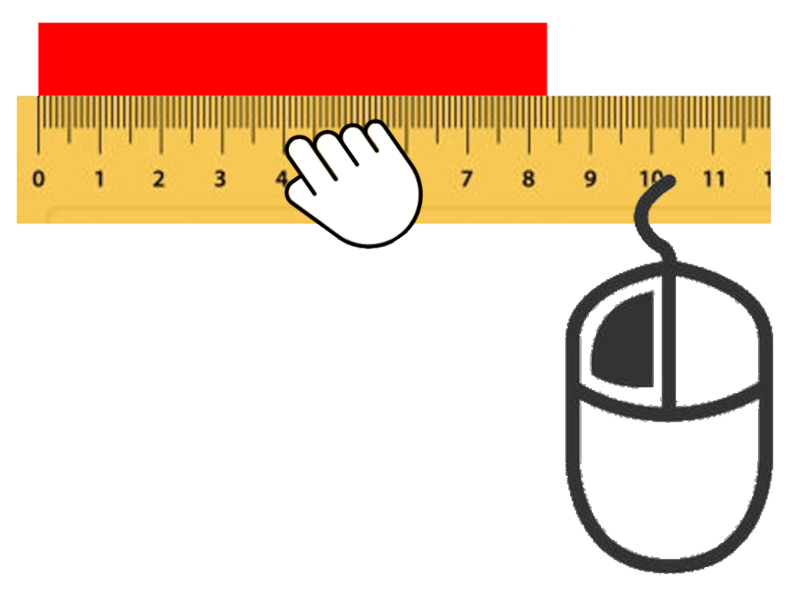
Wenn wir das Lineal am Ursprung anlegen, merken wir sofort, wie schwierig es ist, die Null exakt mit dem linken Rand auszurichten. Ähnlich verhält es sich am rechten Rand: Er liegt zwischen zwei Markierungen, und wir sind gezwungen, den entsprechenden Wert zu schätzen:

Schließlich schätzen wir den Anteil des Zwischenraums ab und geben einen Wert mit einer Zehntel Millimeter an. Dabei wird uns bewusst, dass wir uns auf der Skala von Zehntelmillimetern bewegen, ohne überhaupt Hundertstel zu berücksichtigen.Daraus schließen wir, dass jedes Messinstrument (nicht nur zur Längenmessung) eine inhärente Begrenzung besitzt. Aus diesem Grund sollten Messwerte stets zusammen mit ihrer Unsicherheit angegeben werden. Dies kann geschehen, indem man dem Wert einen Bereich zuordnet, zum Beispiel: [27,1; 27,7], oder indem man den Mittelwert (27,4) verwendet und angibt, wie viel man hinzufügen oder abziehen muss, um den Bereich zu bestimmen:27,4±0,3Dieses Prinzip gilt nicht nur für einzelne Messungen, sondern auch für die Berechnung von Entfernungen, wie im Modell anhand eines Beispiels gezeigt wird.
ID:(3, 0)
Referenz zur Längenmessung
Beschreibung 
Jede Messung entspricht einem Vergleich eines bestimmten Werts mit einem Referenzmuster, woraus der Wert in der entsprechenden Einheit abgeleitet wird.
Im Laufe der Zeit haben sich diese Muster weiterentwickelt und eine größere Genauigkeit erreicht. Beispiele sind:

Gefälschte Kopie des ersten Metermaßstabs (beachten Sie die falsche Schreibweise), versiegelt im Fundament eines Gebäudes, 36 rue de Vaugirard, Paris, Ken Eckert (Wikimedia Commons)
Eine Kopie des vorläufigen Meters, installiert von 1796 bis 1797, an der Wand eines Gebäudes in der 36 Rue de Vaugirard, Paris

Historische niederländische Nachbildungen metrischer Maßstäbe in der Sammlung des Rijksmuseums, Amsterdam: Eisenzähler mit Gehäuse (konstruiert von Étienne Lenoir, 1799; Katalognummer NG-2001-16-C-8), Kupfergrab-Kilogramm mit Gehäuse (1798; Katalognummer NG-2001-16-D-9), Kupfer-Volumenmaße ( 1829; Katalognummer NG-2001-16-B-28)., Yerpo (Wikimedia Commons)
Im Jahr 1799 fertigte Étienne Lenoir die Platin- und zwölf Eisenstandards des Meters an.

Rule (Geändert von Wikimedia Commons, Ein Lineal, das zwei übliche Längeneinheiten darstellt, den Zentimeter und den Zoll)
Das Gradmesser enthält eine längsgraduierte Skala aus rostfreiem Stahl, um zu verhindern, dass die Bildung von Rost das Lesen beeinträchtigt oder die Skala löscht.
ID:(2238, 0)
Lineal oder Maßband
Beschreibung 
Ein Lineal oder ein Maßband sind beide Methoden zur Messung von Längen. Ein Lineal ist ein flaches Messgerät, das mit Längeneinheiten wie Zoll, Zentimeter oder Millimeter markiert ist. Ein Maßband ist ein flexibles Messgerät, das mit Längeneinheiten markiert ist. Maßbänder sind in der Regel genauer als Lineale, da sie gekrümmte Oberflächen messen und auf größere Längen ausgedehnt werden können.

ID:(12508, 0)
Laser-Entfernungsmesser
Beschreibung 
Ein Laserentfernungsmesser ist ein Gerät, das einen Laserstrahl verwendet, um die Entfernung zwischen zwei Punkten zu messen. Es funktioniert, indem es einen Laserimpuls sendet, der von dem zu messenden Objekt reflektiert und dann vom Entfernungsmesser detektiert wird. Die Zeit, die der Laserimpuls benötigt, um von dem Entfernungsmesser zum Objekt und zurück zu reisen, kann dann verwendet werden, um die Entfernung zwischen den beiden Punkten zu berechnen. Laserentfernungsmesser werden häufig in Vermessungen, Navigation und anderen Anwendungen eingesetzt, in denen präzise Messungen erforderlich sind.

ID:(481, 0)
GPS (Global Positioning System)
Beschreibung 
Das Global Positioning System (GPS) ist ein satellitengestütztes Navigationssystem, das ein Netzwerk von 24 Satelliten verwendet, die die Erde umkreisen, um die exakte Position einer Person oder eines Objekts auf dem Planeten zu bestimmen. GPS-Empfänger berechnen die Entfernung zu jedem Satelliten, indem sie die Zeit messen, die die Signale benötigen, um vom Satelliten zum Empfänger zu gelangen. Sobald diese Entfernungen bekannt sind, kann der Empfänger einen Prozess namens Trilateration verwenden, um seine exakte Position, einschließlich Längen- und Breitengrad sowie Höhe, zu berechnen. Dies kann verwendet werden, um die Entfernungen zwischen zwei Standorten zu messen, sowie die Länge einer von einer Person oder einem Objekt zurückgelegten Strecke.

ID:(474, 0)
Position
Beschreibung 
Die Position ($s$) eines Objekts in einem eindimensionalen System bezieht sich auf den Standort des Objekts in Bezug auf einen Referenzpunkt. Diese Lage wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt ausgedrückt. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.

ID:(15, 0)
Ausgangsposition
Beschreibung 
Die Ausgangsstellung ($s_0$) ist der Startort eines Objekts, bevor sich dieses bewegt. Diese Position wird als Entfernung zwischen dem Objekt und dem Ursprungspunkt definiert. Diese Entfernung kann eine Gerade auf einem kartesischen Koordinatensystem sein oder einem gekrümmten Pfad folgen.

ID:(10302, 0)
Zurückgelegte Strecke
Beschreibung 
Die Zurückgelegte Strecke in einer Zeit ($\Delta s$) eines Objekts wird gemessen, indem man die Entfernung zwischen zwei spezifischen Punkten entlang einer Trajektorie misst. Diese Trajektorie kann eine Gerade auf einem kartesischen Koordinatensystem oder ein gekrümmter Pfad sein. Die Entfernung wird berechnet, indem man die Länge der Trajektorie zwischen den beiden Start- und Endpunkten misst.

ID:(9495, 0)
Position in einer Dimension
Modell 
Um die Position eines Objekts zu bestimmen, wird ein Koordinatensystem eingeführt, das es ermöglicht, einen Ursprungspunkt festzulegen und die Position durch die Messung der Entfernung entlang einer geraden Linie oder einer Kurve zu definieren. Demzufolge entspricht die Einheit der Position einer Längenmessung, wie Kilometer, Meter, Zentimeter und so weiter. Die Wahl des Koordinatensystems ist flexibel und erfolgt, um die Modellierung und die zugehörigen Berechnungen so weit wie möglich zu vereinfachen. Zum Beispiel, wenn sich das Objekt entlang einer Strecke bewegt, die nicht unbedingt gerade verläuft, ist es vorteilhaft, das Koordinatensystem entlang dieser Strecke zu definieren. In diesem speziellen Fall wird die Position als die Entfernung vom Ursprung oder dem Startpunkt der Strecke definiert.
Variablen
Berechnungen
Berechnungen
Gleichungen
Wenn man von die Ausgangsstellung ($s_0$) ausgeht und die Zurückgelegte Strecke in einer Zeit ($\Delta s$) berechnen möchte, muss ein Wert für die Position ($s$) festgelegt werden.
In einem eindimensionalen System erhält man die Zurückgelegte Strecke in einer Zeit ($\Delta s$), indem man die Ausgangsstellung ($s_0$) von die Position ($s$) subtrahiert. Das ergibt:
| $ \Delta s = s - s_0 $ |
(ID 4352)
Beispiele
Die Infinitesimal zurückgelegte Strecke ($ds$) zwischen zwei Punkten ist ein Abstand, der so klein ist, dass sich die Bewegung zwischen den beiden Punkten als gleichf rmig betrachtet werden kann.
Allgemein werden Differenzen einer Variablen dadurch dargestellt, dass dem entsprechenden Buchstaben das Symbol $\Delta$ vorangestellt wird. Die Ver nderung der Position $s$ wird also als $\Delta s$ ausgedr ckt. F r infinitesimale Ver nderungen wird anstelle von $\Delta$ ein $d$ verwendet, sodass eine infinitesimale Ver nderung in der Position als $ds$ dargestellt wird.
(ID 14451)
Um die Bewegung eines K rpers zu modellieren, ist es notwendig zu beschreiben, wie er sich bewegt, das hei t den Weg und die Richtung, in die er sich bewegt. Wenn der Weg gekr mmt ist, stimmt der Vektor zwischen der aktuellen und zuk nftigen Position nicht notwendigerweise mit dem tats chlichen Weg berein, es sei denn, der Weg ist infinitesimal. In einem solchen Fall ist die Abweichung von dem Segment vernachl ssigbar, und der Bogen entspricht dem tangentialen Vektor der Kurve.
(ID 14452)
In der Physik bezieht sich die Position auf den Ort eines Objekts im Raum in Bezug auf einen Referenzpunkt oder Ursprung. Es ist ein grundlegendes Konzept, das zur Beschreibung der Bewegung von Objekten verwendet wird und oft als Vektorgr e mit Gr e und Richtung dargestellt wird.Die Position kann mithilfe eines Koordinatensystems beschrieben werden, wie beispielsweise einem kartesischen Koordinatensystem, das drei Achsen (x, y und z) verwendet, um die Position eines Objekts im dreidimensionalen Raum zu definieren. Die Position eines Objekts kann in Einheiten von L nge wie Metern, Fu oder Kilometern gemessen und ausgedr ckt werden.Die nderung der Position eines Objekts im Laufe der Zeit wird als Verschiebung bezeichnet, die ebenfalls eine Vektorgr e ist und die Richtung der Bewegung des Objekts ber cksichtigt. Position, Verschiebung und andere damit zusammenh ngende Konzepte sind zentral f r das Studium der Mechanik, die eine Disziplin der Physik ist, die sich mit der Bewegung von Objekten und den Kr ften, die diese Bewegung verursachen, befasst.
(ID 14449)
ID:(607, 0)
