Accélération constante, deux étapes
Storyboard 
Dans le cas d'un mouvement accéléré en deux étapes, lors de la transition de la première à la deuxième accélération, la vitesse finale de la première étape devient la vitesse initiale de la deuxième. Il en va de même pour la position, où la position finale de la première étape est égale à la position initiale de la deuxième étape.Contrairement au modèle à deux vitesses, ce modèle ne présente pas de problèmes de discontinuité, à l'exception du fait que l'accélération peut changer brusquement, ce qui est techniquement possible mais souvent peu réaliste.
ID:(1435, 0)
Mouvement en deux étapes
Concept 
Dans un scénario de mouvement en deux étapes, d'abord l'objet modifie sa vitesse de a différence de vitesse dans la première étape ($\Delta v_1$) pendant un intervalle de temps de un temps écoulé dans la première étape ($\Delta t_1$) avec une accélération de une accélération lors de la première étape ($a_1$).
| $ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$ |
Ensuite, dans la deuxième étape, il progresse en modifiant sa vitesse de a différence de vitesse dans la deuxième étape ($\Delta v_2$) pendant un intervalle de temps de le temps passé dans la deuxième étape ($\Delta t_2$) avec une accélération de a accélération pendant la deuxième étape ($a_2$).
| $ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$ |
Lorsque cela est représenté graphiquement, nous obtenons un diagramme de vitesse et de temps comme montré ci-dessous :

La clé ici est que les valeurs le temps écoulé dans la première étape ($\Delta t_1$) et le temps passé dans la deuxième étape ($\Delta t_2$) sont séquentielles, tout comme les valeurs a différence de vitesse dans la première étape ($\Delta v_1$) et a différence de vitesse dans la deuxième étape ($\Delta v_2$).
ID:(4829, 0)
Evolution de la vitesse
Concept 
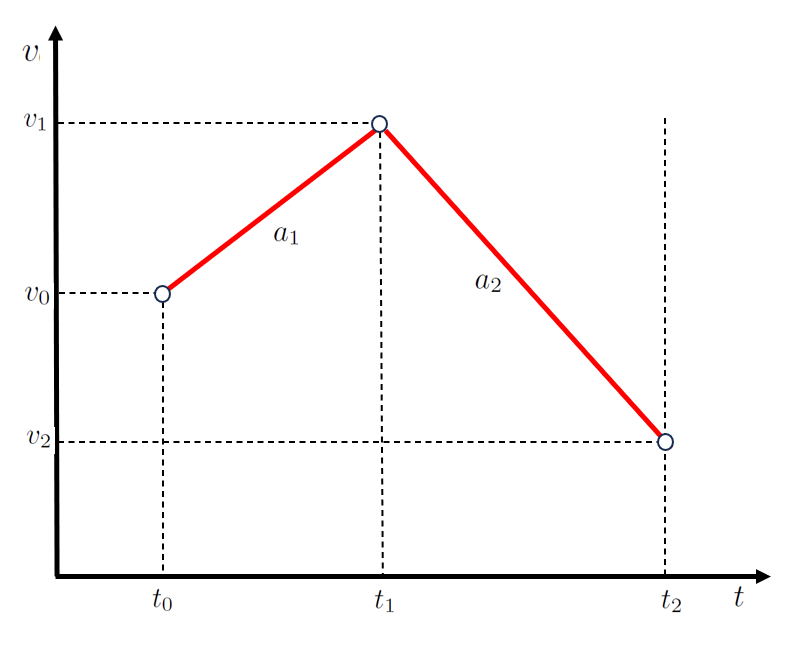
Dans le cas d'un mouvement en deux étapes, la première étape peut être décrite par une fonction impliquant les points le temps initial ($t_0$), le temps final de la première et départ de la deuxième étape ($t_1$), a vitesse initiale ($v_0$) et a vitesse du premier étage ($v_1$), représentée par une droite avec une pente de a accélération lors de la première étape ($a_1$) :
| $ v_1 = v_0 + a_1 ( t_1 - t_0 )$ |
Pour la deuxième étape, définie par les points a vitesse du premier étage ($v_1$), a vitesse du deuxième étage ($v_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), une deuxième droite avec une pente de a accélération pendant la deuxième étape ($a_2$) est employée :
| $ v_2 = v_1 + a_2 ( t_2 - t_1 )$ |
qui est représentée comme suit :
ID:(4357, 0)
Evolution de la position
Concept 
Dans le cas d'un mouvement en deux étapes, la position à laquelle se termine la première étape coïncide avec la position au début de la deuxième étape ($s_1$).
De même, le moment où se termine la première étape coïncide avec le début de la deuxième étape ($t_1$).
Puisque le mouvement est défini par l'accélération éprouvée, la vitesse atteinte à la fin de la première étape doit correspondre à la vitesse initiale de la deuxième étape ($v_1$).
En cas d'accélération constante, lors de la première étape, le première position finale et départ de la deuxième étape ($s_1$) dépend de a vitesse ($s_0$), a vitesse initiale ($v_0$), a accélération lors de la première étape ($a_1$), le temps final de la première et départ de la deuxième étape ($t_1$) et le temps initial ($t_0$), comme suit :
| $ s_1 = s_0 + v_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} a_1 ( t_1 - t_0 )^2$ |
Pour la deuxième étape, a position finale de la deuxième étape ($s_2$) dépend de le première position finale et départ de la deuxième étape ($s_1$), a vitesse du premier étage ($v_1$), a accélération pendant la deuxième étape ($a_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), comme suit :
| $ s_2 = s_1 + v_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} a_2 ( t_2 - t_1 )^2$ |
qui est représenté comme suit :

ID:(2254, 0)
Modèle
Concept 
Si le mouvement comprend deux étapes avec différentes accélérations constantes $a_1$ et $a_2$ :
• Il commence à un moment $t_0$ en une position $s_0$ avec une vitesse $v_0$.
• Il se termine à un moment $t_2$ en une position $s_2$ avec une vitesse $v_2$.
La clé réside dans la transition d'une étape à l'autre :
• Les vitesses varient en fonction des accélérations mais sont égales au point de transition entre les étapes ($v_1$).
• Les positions varient en fonction de la vitesse mais sont égales au point de transition entre les étapes ($s_1$).
• Les temps sont égaux au point de transition entre les étapes ($t_1$).
Ceci est résumé dans les graphiques suivants :
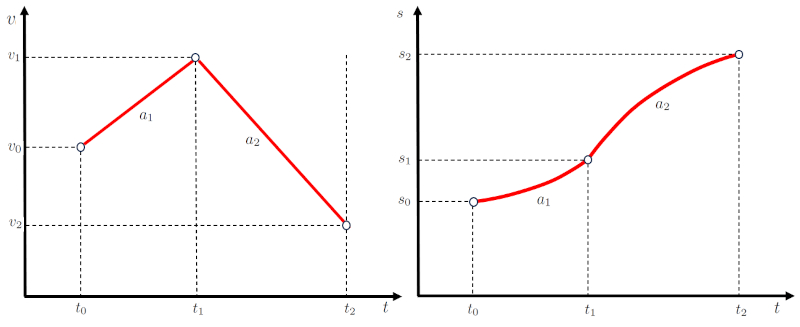
Les équations qui satisfont ces relations donnent lieu au modèle suivant, qui permet de calculer n'importe quel scénario :
ID:(15400, 0)
Accélération constante, deux étapes
Modèle 
Dans le cas d'un mouvement accéléré en deux étapes, lors de la transition de la première à la deuxième accélération, la vitesse finale de la première étape devient la vitesse initiale de la deuxième. Il en va de même pour la position, où la position finale de la première étape est égale à la position initiale de la deuxième étape. Contrairement au modèle à deux vitesses, ce modèle ne présente pas de problèmes de discontinuité, à l'exception du fait que l'accélération peut changer brusquement, ce qui est techniquement possible mais souvent peu réaliste.
Variables
Calculs
Calculs
Équations
Dans le cas o a accélération constante ($a_0$) est gal a accélération moyenne ($\bar{a}$), il sera gal
| $ a_0 = \bar{a} $ |
.
Ainsi, si nous consid rons a différence de vitesse ($\Delta v$) comme tant
| $ dv \equiv v - v_0 $ |
et le temps écoulé ($\Delta t$) comme tant
| $ \Delta t \equiv t - t_0 $ |
,
alors l' quation pour a accélération constante ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
peut tre crite comme
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
ainsi, en isolant, nous obtenons
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Dans le cas o a accélération constante ($a_0$) est gal a accélération moyenne ($\bar{a}$), il sera gal
| $ a_0 = \bar{a} $ |
.
Ainsi, si nous consid rons a différence de vitesse ($\Delta v$) comme tant
| $ dv \equiv v - v_0 $ |
et le temps écoulé ($\Delta t$) comme tant
| $ \Delta t \equiv t - t_0 $ |
,
alors l' quation pour a accélération constante ($a_0$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
peut tre crite comme
$a_0 = \bar{a} = \displaystyle\frac{\Delta v}{\Delta t} = \displaystyle\frac{v - v_0}{t - t_0}$
ainsi, en isolant, nous obtenons
| $ v = v_0 + a_0 ( t - t_0 )$ |
.
(ID 3156)
Dans le cas de a accélération constante ($a_0$), a vitesse ($v$) en fonction de le temps ($t$) est une droite passant par le temps initial ($t_0$) et a vitesse initiale ($v_0$) selon :
| $ v = v_0 + a_0 ( t - t_0 )$ |
Comme a distance parcourue en un temps ($\Delta s$) correspond l'aire sous la courbe de vitesse-temps, nous pouvons additionner la contribution du rectangle :
$v_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Ainsi, avec a position ($s$) et a vitesse ($s_0$), nous obtenons :
| $ \Delta s = s - s_0 $ |
Ce qui donne finalement :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Dans le cas de a accélération constante ($a_0$), a vitesse ($v$) en fonction de le temps ($t$) est une droite passant par le temps initial ($t_0$) et a vitesse initiale ($v_0$) selon :
| $ v = v_0 + a_0 ( t - t_0 )$ |
Comme a distance parcourue en un temps ($\Delta s$) correspond l'aire sous la courbe de vitesse-temps, nous pouvons additionner la contribution du rectangle :
$v_0(t-t_0)$
et du triangle :
$\displaystyle\frac{1}{2}a_0(t-t_0)^2$
Ainsi, avec a position ($s$) et a vitesse ($s_0$), nous obtenons :
| $ \Delta s = s - s_0 $ |
Ce qui donne finalement :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
(ID 3157)
Si l'on r sout les quations pour le temps ($t$) et le temps initial ($t_0$) dans l' quation de a vitesse ($v$), qui d pend de a vitesse initiale ($v_0$) et a accélération constante ($a_0$) :
| $ v = v_0 + a_0 ( t - t_0 )$ |
nous obtenons :
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Ensuite, en rempla ant cette expression dans l' quation de a position ($s$) avec a vitesse ($s_0$) :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
nous obtenons une expression du chemin parcouru en fonction de la vitesse :
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
Si l'on r sout les quations pour le temps ($t$) et le temps initial ($t_0$) dans l' quation de a vitesse ($v$), qui d pend de a vitesse initiale ($v_0$) et a accélération constante ($a_0$) :
| $ v = v_0 + a_0 ( t - t_0 )$ |
nous obtenons :
$t - t_0= \displaystyle\frac{v - v_0}{a_0}$
Ensuite, en rempla ant cette expression dans l' quation de a position ($s$) avec a vitesse ($s_0$) :
| $ s = s_0 + v_0 ( t - t_0 )+\displaystyle\frac{1}{2} a_0 ( t - t_0 )^2$ |
nous obtenons une expression du chemin parcouru en fonction de la vitesse :
| $ s = s_0 +\displaystyle\frac{ v ^2- v_0 ^2}{2 a_0 }$ |
(ID 3158)
La d finition de a accélération moyenne ($\bar{a}$) est consid r e comme la relation entre a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$). C'est- -dire,
| $ dv \equiv v - v_0 $ |
et
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme a accélération centrifuge ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
pendant cet intervalle de temps.
(ID 3678)
La d finition de a accélération moyenne ($\bar{a}$) est consid r e comme la relation entre a différence de vitesse ($\Delta v$) et le temps écoulé ($\Delta t$). C'est- -dire,
| $ dv \equiv v - v_0 $ |
et
| $ \Delta t \equiv t - t_0 $ |
La relation entre les deux est d finie comme a accélération centrifuge ($a_c$)
| $ \bar{a} \equiv\displaystyle\frac{ \Delta v }{ \Delta t }$ |
pendant cet intervalle de temps.
(ID 3678)
Si l’on part de a vitesse ($s_0$) et que l’on souhaite calculer a distance parcourue en un temps ($\Delta s$), il est nécessaire de définir une valeur pour a position ($s$).
Dans un système unidimensionnel, a distance parcourue en un temps ($\Delta s$) est simplement obtenu en soustrayant a vitesse ($s_0$) de a position ($s$), ce qui donne :
| $ \Delta s = s - s_0 $ |
(ID 4352)
Si l’on part de a vitesse ($s_0$) et que l’on souhaite calculer a distance parcourue en un temps ($\Delta s$), il est nécessaire de définir une valeur pour a position ($s$).
Dans un système unidimensionnel, a distance parcourue en un temps ($\Delta s$) est simplement obtenu en soustrayant a vitesse ($s_0$) de a position ($s$), ce qui donne :
| $ \Delta s = s - s_0 $ |
(ID 4352)
(ID 4355)
(ID 4355)
Exemples
(ID 15397)
Dans un sc nario de mouvement en deux tapes, d'abord l'objet modifie sa vitesse de a différence de vitesse dans la première étape ($\Delta v_1$) pendant un intervalle de temps de un temps écoulé dans la première étape ($\Delta t_1$) avec une acc l ration de une accélération lors de la première étape ($a_1$).
| $ a_1 \equiv\displaystyle\frac{ \Delta v_1 }{ \Delta t_1 }$ |
Ensuite, dans la deuxi me tape, il progresse en modifiant sa vitesse de a différence de vitesse dans la deuxième étape ($\Delta v_2$) pendant un intervalle de temps de le temps passé dans la deuxième étape ($\Delta t_2$) avec une acc l ration de a accélération pendant la deuxième étape ($a_2$).
| $ a_2 \equiv\displaystyle\frac{ \Delta v_2 }{ \Delta t_2 }$ |
Lorsque cela est repr sent graphiquement, nous obtenons un diagramme de vitesse et de temps comme montr ci-dessous :

La cl ici est que les valeurs le temps écoulé dans la première étape ($\Delta t_1$) et le temps passé dans la deuxième étape ($\Delta t_2$) sont s quentielles, tout comme les valeurs a différence de vitesse dans la première étape ($\Delta v_1$) et a différence de vitesse dans la deuxième étape ($\Delta v_2$).
(ID 4829)
Dans le cas d'un mouvement en deux tapes, la premi re tape peut tre d crite par une fonction impliquant les points le temps initial ($t_0$), le temps final de la première et départ de la deuxième étape ($t_1$), a vitesse initiale ($v_0$) et a vitesse du premier étage ($v_1$), repr sent e par une droite avec une pente de a accélération lors de la première étape ($a_1$) :
| $ v_1 = v_0 + a_1 ( t_1 - t_0 )$ |
Pour la deuxi me tape, d finie par les points a vitesse du premier étage ($v_1$), a vitesse du deuxième étage ($v_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), une deuxi me droite avec une pente de a accélération pendant la deuxième étape ($a_2$) est employ e :
| $ v_2 = v_1 + a_2 ( t_2 - t_1 )$ |
qui est repr sent e comme suit :

(ID 4357)
Dans le cas d'un mouvement en deux tapes, la position laquelle se termine la premi re tape co ncide avec la position au d but de la deuxi me tape ($s_1$).
De m me, le moment o se termine la premi re tape co ncide avec le d but de la deuxi me tape ($t_1$).
Puisque le mouvement est d fini par l'acc l ration prouv e, la vitesse atteinte la fin de la premi re tape doit correspondre la vitesse initiale de la deuxi me tape ($v_1$).
En cas d'acc l ration constante, lors de la premi re tape, le première position finale et départ de la deuxième étape ($s_1$) d pend de a vitesse ($s_0$), a vitesse initiale ($v_0$), a accélération lors de la première étape ($a_1$), le temps final de la première et départ de la deuxième étape ($t_1$) et le temps initial ($t_0$), comme suit :
| $ s_1 = s_0 + v_0 ( t_1 - t_0 )+\displaystyle\frac{1}{2} a_1 ( t_1 - t_0 )^2$ |
Pour la deuxi me tape, a position finale de la deuxième étape ($s_2$) d pend de le première position finale et départ de la deuxième étape ($s_1$), a vitesse du premier étage ($v_1$), a accélération pendant la deuxième étape ($a_2$), le temps final de la première et départ de la deuxième étape ($t_1$) et le heure de fin de la deuxième étape ($t_2$), comme suit :
| $ s_2 = s_1 + v_1 ( t_2 - t_1 )+\displaystyle\frac{1}{2} a_2 ( t_2 - t_1 )^2$ |
qui est repr sent comme suit :

(ID 2254)
Si le mouvement comprend deux tapes avec diff rentes acc l rations constantes $a_1$ et $a_2$ :
• Il commence un moment $t_0$ en une position $s_0$ avec une vitesse $v_0$.
• Il se termine un moment $t_2$ en une position $s_2$ avec une vitesse $v_2$.
La cl r side dans la transition d'une tape l'autre :
• Les vitesses varient en fonction des acc l rations mais sont gales au point de transition entre les tapes ($v_1$).
• Les positions varient en fonction de la vitesse mais sont gales au point de transition entre les tapes ($s_1$).
• Les temps sont gaux au point de transition entre les tapes ($t_1$).
Ceci est r sum dans les graphiques suivants :

Les quations qui satisfont ces relations donnent lieu au mod le suivant, qui permet de calculer n'importe quel sc nario :
(ID 15400)
ID:(1435, 0)
