Benützer:


Hebelgesetz
Storyboard

Das Hebelgesetz entspricht einem System, das zwei gleichen und entgegengesetzten Drehmomenten ausgesetzt ist, mit denen das System im Gleichgewicht bleibt.

>Modell

ID:(1457, 0)


Hebelgesetz
Modell

Das Hebelgesetz entspricht einem System, das zwei gleichen und entgegengesetzten Drehmomenten ausgesetzt ist, mit denen das System im Gleichgewicht bleibt.

Variablen
Symbol
Text
Variable
Wert
Einheiten
Berechnen
MKS-Wert
MKS-Einheiten
$d_1$
d_1
Abstand Kraft - Achse (Arm) 1
m
$d_2$
d_2
Abstand Kraft - Achse (Arm) 2
m
$T_1$
T_1
Drehmoment 1
N m
$T_2$
T_2
Drehmoment 2
N m
$F_1$
F_1
Kraft 1
N
$F_2$
F_2
Kraft 2
N
$m_1$
m_1
Masse 1
kg
$m_2$
m_2
Masse 2
kg

Berechnungen

Zuerst die Gleichung auswählen:   zu ,  dann die Variable auswählen:   zu 
Symbol
Gleichung
Gelöst
Übersetzt

Berechnungen

Symbol
Gleichung
Gelöst
Übersetzt

 Variable   Gegeben   Berechnen   Ziel :   Gleichung   Zu verwenden


Gleichungen

Im Falle einer Waage wirkt auf jeden Arm eine Gravitationskraft, die ein Drehmoment erzeugt

$ T = r F $



Wenn die L ngen der Arme $d_i$ betragen und die Kr fte $F_i$ mit $i=1,2$ sind, verlangt die Gleichgewichtsbedingung, dass die Summe der Drehmomente null ist:

$\displaystyle\sum_i \vec{T}_i=0$



Daher, unter Ber cksichtigung, dass das Vorzeichen jedes Drehmoments von der Richtung abh ngt, in der es eine Rotation induziert,

$d_1F_1-d_2F_2=0$



was zu

$ d_1 F_1 = d_2 F_2 $

f hrt.

(ID 3250)

Si se deriva en el tiempo la relaci n para el momento angular

$ L = r p $



para el caso de que el radio sea constante

$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$



por lo que

$ T = r F $

(ID 4431)

Si se deriva en el tiempo la relaci n para el momento angular

$ L = r p $



para el caso de que el radio sea constante

$T=\displaystyle\frac{dL}{dt}=r\displaystyle\frac{dp}{dt}=rF$



por lo que

$ T = r F $

(ID 4431)

Beispiele


(ID 15845)

Da das durch die Schwerkraft erzeugte Drehmoment und der Hebelarm

$ T = r F $



auf jeder Seite der Waage vorhanden sind, muss es im Gleichgewichtszustand aufgehoben werden, um ein Gleichgewicht zu erreichen:



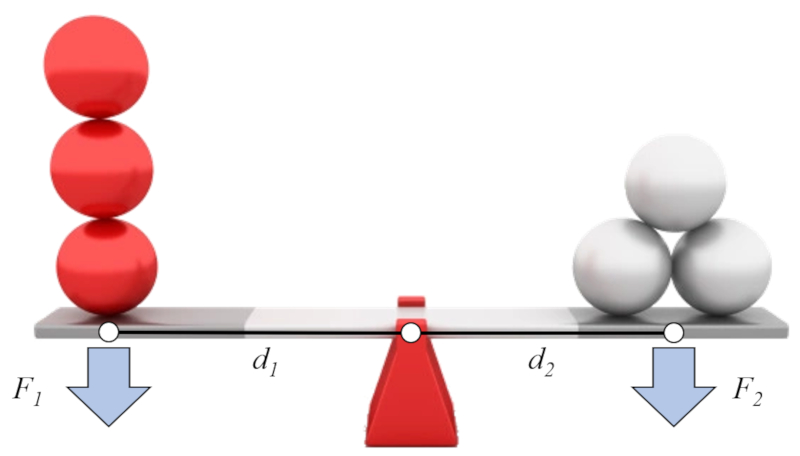
Wenn wir annehmen, dass auf der einen Seite die Kraft 1 ($F_1$) und der Abstand Kraft - Achse (Arm) 1 ($d_1$) und auf der anderen Seite die Kraft 2 ($F_2$) und der Abstand Kraft - Achse (Arm) 2 ($d_2$) vorhanden sind, kann das sogenannte Hebelgesetz wie folgt aufgestellt werden:

$ d_1 F_1 = d_2 F_2 $

(ID 15847)


(ID 15846)

ID:(1457, 0)