Usuario:
Teorema de Steiner
Storyboard 
Por lo general los momentos de inercia se calculan respecto de ejes que pasan por el centro de masa. Sin embargo en muchas situaciones la rotación ocurre en torno de otro eje. En ese caso se puede calcular el momento de inercia en trono de cualquier eje paralelo en función del teorema de Steiner para lo que se necesita solo el momento de inercia respecto del centro de masa, la masa y la distancia entre el eje real y el que pasa por el centro de masa.
ID:(1456, 0)
Aplicación del teorema de Steiner para un cilindro, eje $\parallel$
Imagen
Para un cilindro con un eje paralelo al eje del cilindro:
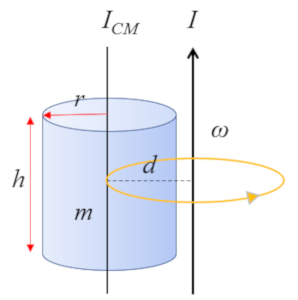
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
el cálculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11551, 0)
Aplicación del teorema de Steiner para un cilindro, eje $\perp$
Imagen
Para un cilindro con un eje perpendicular al eje del cilindro:
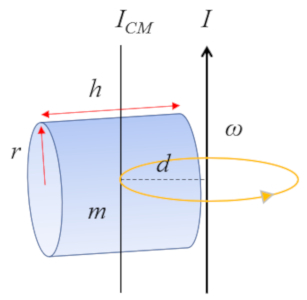
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
el cálculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11552, 0)
Aplicación del teorema de Steiner para un paralelepipedo recto
Imagen
Para un paralelepípedo recto con un eje paralelo a una arista:
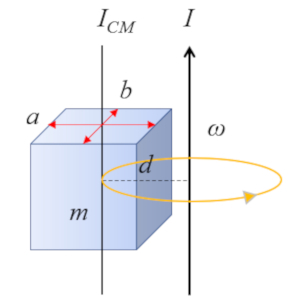
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
el cálculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente fórmula
| $ I = I_{CM} + m d ^2$ |
.
ID:(11554, 0)
Aplicación del teorema de Steiner para una esfera
Imagen
Para una esfera con un eje a una distancia del centro de esta:
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
el cálculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente fórmula distancia centro de masa y eje $m$, masa del cuerpo $kg$, momento de inercia del centro de masa $kg m^2$ y momento de inercia para eje que no pasa por el CM $kg m^2$
| $ I = I_{CM} + m d ^2$ |
.
ID:(11553, 0)
Teorema de Steiner
Modelo
Por lo general los momentos de inercia se calculan respecto de ejes que pasan por el centro de masa. Sin embargo en muchas situaciones la rotación ocurre en torno de otro eje. En ese caso se puede calcular el momento de inercia en trono de cualquier eje paralelo en función del teorema de Steiner para lo que se necesita solo el momento de inercia respecto del centro de masa, la masa y la distancia entre el eje real y el que pasa por el centro de masa.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
Ejemplos
Para un cilindro con un eje paralelo al eje del cilindro:
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{2} m r_c ^2$ |
el c lculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente f rmula
| $ I = I_{CM} + m d ^2$ |
.
(ID 11551)
Para un cilindro con un eje perpendicular al eje del cilindro:
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( h ^2+3 r_c ^2)$ |
el c lculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente f rmula
| $ I = I_{CM} + m d ^2$ |
.
(ID 11552)
Para un paralelep pedo recto con un eje paralelo a una arista:
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{1}{12} m ( a ^2+ b ^2)$ |
el c lculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente f rmula
| $ I = I_{CM} + m d ^2$ |
.
(ID 11554)
Para una esfera con un eje a una distancia del centro de esta:
cuyo momento de inercia con respecto al centro de masa (CM) se define como
| $ I_{CM} =\displaystyle\frac{2}{5} m r_e ^2$ |
el c lculo del momento de inercia se puede realizar utilizando el teorema de Steiner con la siguiente f rmula distancia centro de masa y eje $m$, masa del cuerpo $kg$, momento de inercia del centro de masa $kg m^2$ y momento de inercia para eje que no pasa por el CM $kg m^2$
| $ I = I_{CM} + m d ^2$ |
.
(ID 11553)
ID:(1456, 0)