Fuerza de un resorte
Storyboard 
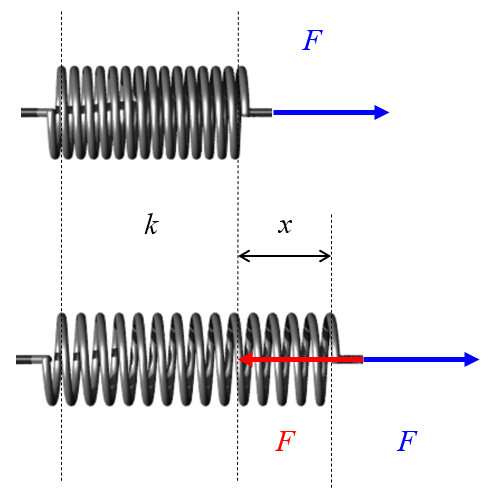
La fuerza generada por un resorte es directamente proporcional a su elongación.
La constante de proporcionalidad se conoce como la constante del resorte o constante de Hooke. De igual manera, la relación de esta fuerza se denomina Ley de Hooke.
ID:(1414, 0)
Fuerza de un resorte
Storyboard 
La fuerza generada por un resorte es directamente proporcional a su elongación. La constante de proporcionalidad se conoce como la constante del resorte o constante de Hooke. De igual manera, la relación de esta fuerza se denomina Ley de Hooke.
Variables
Cálculos
Cálculos
Ecuaciones
Dado que el momento ($p$) se define con la masa inercial ($m_i$) y la velocidad ($v$),
Si la masa inercial ($m_i$) es igual a la masa inicial ($m_0$), entonces podemos derivar el momento respecto al tiempo y obtener la fuerza con masa constante ($F$):
$F=\displaystyle\frac{d}{dt}p=m_i\displaystyle\frac{d}{dt}v=m_ia$
Por lo tanto, llegamos a la conclusi n de que
Given that la fuerza con masa constante ($F$) is equal to la fuerza elástica ($F_k$) minus la fuerza gravitacional ($F_g$):
If we consider that la fuerza con masa constante ($F$) with la masa inercial ($m_i$) and la aceleración instantanea ($a$) is
and la fuerza elástica ($F_k$) is with la constante de Hooke ($k$) and la elongación ($u$) is
and that la fuerza gravitacional ($F_g$) is with la masa gravitacional ($m_g$) and la aceleración gravitacional ($g$)
which results in
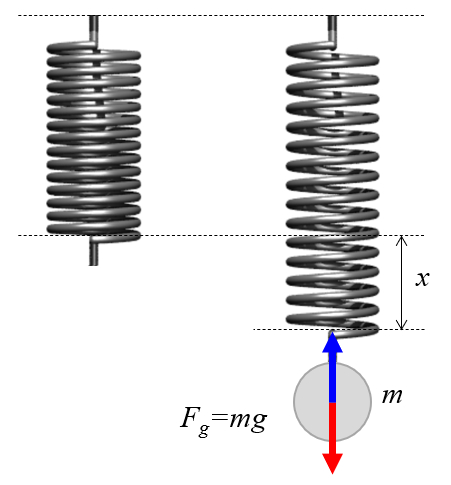
Si se cuelga una masa generando una fuerza
a un resorte este ltimo se dilata hasta generar una fuerza que es
que iguala a la fuerza gravitacional que es
Ejemplos
Un resorte es un alambre retorcido que puede estirarse o comprimirse.
Cuando se realizan estas deformaciones, el resorte genera una fuerza que se opone al movimiento.
Si se mide la fuerza requerida para lograr una determinada elongaci n en el resorte, se observar que ambas son proporcionales:
Se cuelga el resorte en forma vertical y se van a adiendo masas de peso conocido. Luego se mide la elongaci n resultante y se grafica la fuerza frente a la elongaci n. La pendiente de esta relaci n, conocida como constante de elasticidad del resorte o constante de Hooke, depende de las propiedades del resorte.
La linealidad de esta relaci n permite utilizar los resortes como un m todo para medir fuerzas.
La fuerza puede medirse utilizando un resorte, estableciendo una escala proporcional a la elongaci n que indique directamente la fuerza asociada.
El instrumento utilizado para medir la fuerza mediante un resorte se llama dinam metro (la 'dina' es la unidad de fuerza en el sistema cgs - cent metros, gramos, segundos - de tal manera que 10^5 dinas equivalen a un Newton).
Para investigar c mo se estira el resorte, se puede suspender verticalmente y a adir pesos conocidos gradualmente.
La ecuaci n de movimiento se establece con el equilibrio de fuerzas que significa que la fuerza con masa constante ($F$) es igual a la fuerza elástica ($F_k$) menos la fuerza gravitacional ($F_g$):
En el caso en que la masa inercial ($m_i$) es igual a la masa inicial ($m_0$),
la derivada del momento ser igual a la masa multiplicada por la derivada de la velocidad ($v$). Dado que la derivada de la velocidad es la aceleración instantanea ($a$), obtenemos que la fuerza con masa constante ($F$) es igual a
La relaci n entre la fuerza elástica ($F_k$) y la elongaci n la elongación ($u$) se expresa y se conoce como la Ley de Hooke. La constante la constante de Hooke ($k$) se denomina la constante de elasticidad del resorte:
La fuerza gravitacional ($F_g$) se basa en la masa gravitacional ($m_g$) del objeto y en una constante que refleja la intensidad de la gravedad en la superficie del planeta. Esta ltima es identificada por la aceleración gravitacional ($g$), que es igual a $9.8 m/s^2$.
En consecuencia, se concluye que:
La ecuaci n de movimiento se obtiene directamente de la ecuaci n de las fuerzas, donde la fuerza con masa constante ($F$) es igual a la fuerza elástica ($F_k$) menos la fuerza gravitacional ($F_g$):
Esta ecuaci n se expresa en funci n de las distintas fuerzas involucradas, incluyendo la aceleración instantanea ($a$), la elongación del resorte ($x$), la constante de Hooke ($k$), la masa inercial ($m_i$), la masa gravitacional ($m_g$) y la aceleración gravitacional ($g$) de la siguiente manera:
Las masas que Newton utiliz en sus principios est n relacionadas con la inercia de los cuerpos, lo que lleva al concepto de la masa inercial ($m_i$).
La ley de Newton que se vincula con la fuerza entre cuerpos debido a sus masas est relacionada con la gravedad, por lo que se conoce como la masa gravitacional ($m_g$).
De manera emp rica, se ha concluido que ambas masas son equivalentes, y por lo tanto, definimos
Einstein fue quien cuestion esta igualdad y, a partir de esa duda, comprendi por qu ambas 'aparecen' iguales en su teor a de la gravedad. En su argumento, Einstein explic que las masas deforman el espacio, y esta deformaci n del espacio provoca un cambio en el comportamiento de los cuerpos. De esta manera, las masas resultan ser equivalentes. El concepto revolucionario de la curvatura del espacio implica que incluso la luz, que carece de masa, se ve afectada por los cuerpos celestes, lo que contradice la teor a de la gravitaci n de Newton. Esto se demostr experimentalmente al estudiar el comportamiento de la luz durante un eclipse solar. En esta situaci n, los haces de luz se desv an debido a la presencia del sol, lo que permite observar estrellas que se encuentran detr s de l.
El producto de la constante de Hooke ($k$) y la masa inercial ($m_i$) se denomina la frecuencia angular del resorte ($\omega$) y se define como:
La frecuencia angular ($\omega$) es con la período ($T$) igual a
La relación entre la frecuencia angular ($\omega$) y la frecuencia del sonido ($\nu$) se expresa como:
La frecuencia del sonido ($\nu$) representa la cantidad de oscilaciones que ocurren en un segundo. Mientras tanto, la período ($T$) es el tiempo que tarda una sola oscilaci n. Por lo tanto, el n mero de oscilaciones por segundo es:
La frecuencia se expresa en Hertz (Hz).
La variable la amplitud de la oscilación ($x$) evoluciona en el tiempo ($t$) seg n la ecuaci n de movimiento con la frecuencia angular del oscilador ($\omega_0$) y la aceleración gravitacional ($g$), expresada como:
Si suponemos que la amplitud inicial de la oscilación ($x_0$) y la velocidad inicial del oscilador ($v_0$) son la soluci n, podemos escribirlo como:
Para obtener la velocidad del oscilador ($v$), simplemente hay que derivar la amplitud de la oscilación ($x$) con respecto a el tiempo ($t$), lo que nos da:
Por lo tanto, con la amplitud inicial de la oscilación ($x_0$), la velocidad inicial ($v_0$) y la frecuencia angular del oscilador ($\omega_0$), obtenemos:
ID:(1414, 0)