Flujo laminar
Storyboard 
En caso de que el numero de Reynold es muy pequeño el flujo es laminar. Con ello se observa que el flujo se puede representar como una serie de laminas sin la parecencia de torbellinos y que se adapta a las condiciones de borde y fluye en forma armónica.
ID:(879, 0)
Flujo laminar, tinta
Descripción 
Una forma efectiva de visualizar el flujo laminar es mediante la inyección de tinta en un flujo utilizando una aguja delgada que no perturbe dicho flujo. Esta técnica permite observar claramente las capas de fluido deslizándose sin mezclarse entre sí. La tinta se dispersa en el fluido de manera ordenada, creando líneas definidas que revelan la dirección y el patrón del flujo laminar. Esta metodología es ampliamente utilizada en experimentos y demostraciones para ilustrar las características y propiedades del flujo laminar de forma visualmente impactante.

ID:(7059, 0)
Imágenes de flujo laminar
Descripción 
La observación en el laboratorio muestra cómo la tinta dibuja una línea (en este caso roja). Si se repite el experimento en distintas posiciones, se observa un patrón de capas, lo que indica que el flujo es laminar.

Los líquidos que fluyen de forma laminar exhiben un flujo suave, sin la formación de vórtices ni movimientos laterales bruscos.
ID:(7060, 0)
Flujo laminar en torno de una esfera
Descripción 
Un ejemplo de flujo laminar alrededor de una esfera muestra que las capas de líquido se desplazan manteniendo su paralelismo.

Aquí tienes una imagen que ilustra el cálculo del flujo entre dos placas y una esfera/cilindro (enlace a la imagen: http://luxsignifer.blogspot.com/2016/10/hele-shaw-flow-past-circle.html).
Esta situación se produce cuando el número de Reynolds $Re$ es menor que 5.
ID:(1889, 0)
Flujo de miel
Descripción 
Existen líquidos que exhiben un comportamiento peculiar, ya que parecen fluir en cámara lenta. Un ejemplo clásico de este fenómeno es la miel.

La causa subyacente de este comportamiento es la fuerza viscosa que se genera cuando una capa de líquido se desliza o se desplaza con respecto a sus capas adyacentes. Esta fuerza viscosa es proporcional a la variación de la velocidad entre las capas del líquido dividida por el grosor de la capa en consideración.
ID:(1655, 0)
Láminas en la corriente
Concepto 
En el flujo laminar, capas contiguas se desplazan y existe una fuerza generada por la viscosidad entre ellas. La capa más rápida arrastra a su vecina más lenta, mientras que la más lenta restringe el avance de la más rápida.
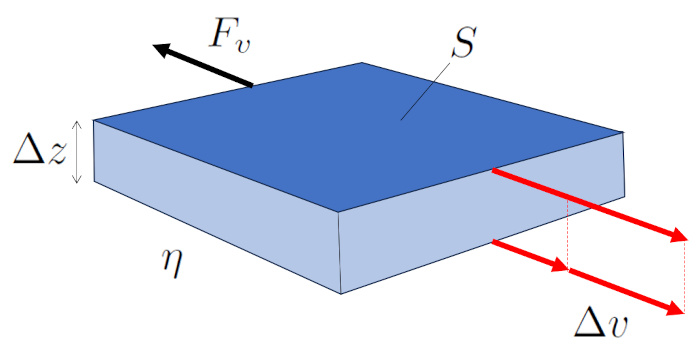
Por lo tanto, la fuerza la fuerza viscosa ($F_v$) generada por unas superficies paralelas ($S$) sobre la otra es una función de una diferencia de velocidad entre superficies ($\Delta v$), una distancia entre las superficies ($\Delta z$) y una viscosidad ($\eta$), como se muestra en la siguiente ecuación:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
y en el diagrama correspondiente:
ID:(7053, 0)
Flujo por un cilindro
Concepto 
El flujo laminar alrededor de un cilindro se puede representar como múltiples capas cilíndricas que se deslizan bajo la influencia de las capas adyacentes. En ese caso, la fuerza viscosa ($F_v$) con el largo de tubo ($\Delta L$), la viscosidad ($\eta$), y las variables la posición radial en cilindro ($r$) y la velocidad en un radio del cilindro ($v$) se expresa como:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
La capa en el borde a un radio del tubo ($R$) no se mueve debido al efecto del borde y, a través de la viscosidad ($\eta$), ralentiza la capa contigua que sí tiene velocidad.
El centro es la parte que se mueve a la velocidad máxima del flujo ($v_{max}$), arrastrando a la capa que lo rodea. A su vez, esta capa arrastra a la siguiente y así sucesivamente hasta llegar a la capa en contacto con la pared del cilindro, que está detenida.
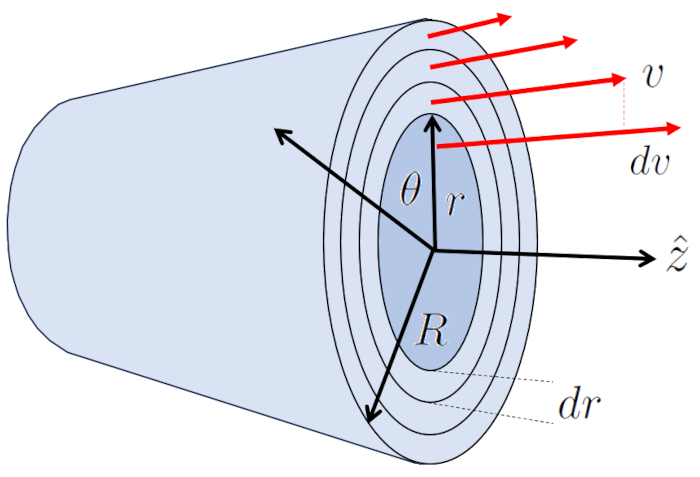
De esta manera, el sistema transfiere energía desde el centro hasta la pared, generando un perfil de velocidad representado por:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
con:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
ID:(7057, 0)
Flujo laminar
Modelo 
En caso de que el numero de Reynold es muy pequeño el flujo es laminar. Con ello se observa que el flujo se puede representar como una serie de laminas sin la parecencia de torbellinos y que se adapta a las condiciones de borde y fluye en forma armónica.
Variables
Cálculos
Cálculos
Ecuaciones
Como
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
y las superficies paralelas ($S$) es
$S=2\pi r \Delta L$
donde el radio de la posición en un tubo ($r$) y el largo de tubo ($\Delta L$), con lo que la la fuerza de resistencia en cilindro ($F_v$) es
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
donde la viscosidad ($\eta$), la variación de la velocidad entre dos radios ($dv$) y el variación del radio en un tubo ($dr$).
(ID 3623)
Ejemplos
Una forma efectiva de visualizar el flujo laminar es mediante la inyecci n de tinta en un flujo utilizando una aguja delgada que no perturbe dicho flujo. Esta t cnica permite observar claramente las capas de fluido desliz ndose sin mezclarse entre s . La tinta se dispersa en el fluido de manera ordenada, creando l neas definidas que revelan la direcci n y el patr n del flujo laminar. Esta metodolog a es ampliamente utilizada en experimentos y demostraciones para ilustrar las caracter sticas y propiedades del flujo laminar de forma visualmente impactante.

(ID 7059)
La observaci n en el laboratorio muestra c mo la tinta dibuja una l nea (en este caso roja). Si se repite el experimento en distintas posiciones, se observa un patr n de capas, lo que indica que el flujo es laminar.

Los l quidos que fluyen de forma laminar exhiben un flujo suave, sin la formaci n de v rtices ni movimientos laterales bruscos.
(ID 7060)
Un ejemplo de flujo laminar alrededor de una esfera muestra que las capas de l quido se desplazan manteniendo su paralelismo.

Aqu tienes una imagen que ilustra el c lculo del flujo entre dos placas y una esfera/cilindro (enlace a la imagen: http://luxsignifer.blogspot.com/2016/10/hele-shaw-flow-past-circle.html).
Esta situaci n se produce cuando el n mero de Reynolds $Re$ es menor que 5.
(ID 1889)
Existen l quidos que exhiben un comportamiento peculiar, ya que parecen fluir en c mara lenta. Un ejemplo cl sico de este fen meno es la miel.

La causa subyacente de este comportamiento es la fuerza viscosa que se genera cuando una capa de l quido se desliza o se desplaza con respecto a sus capas adyacentes. Esta fuerza viscosa es proporcional a la variaci n de la velocidad entre las capas del l quido dividida por el grosor de la capa en consideraci n.
(ID 1655)
En el flujo laminar, capas contiguas se desplazan y existe una fuerza generada por la viscosidad entre ellas. La capa m s r pida arrastra a su vecina m s lenta, mientras que la m s lenta restringe el avance de la m s r pida.
Por lo tanto, la fuerza la fuerza viscosa ($F_v$) generada por unas superficies paralelas ($S$) sobre la otra es una funci n de una diferencia de velocidad entre superficies ($\Delta v$), una distancia entre las superficies ($\Delta z$) y una viscosidad ($\eta$), como se muestra en la siguiente ecuaci n:
| $ F_v =- S \eta \displaystyle\frac{ \Delta v }{ \Delta z }$ |
y en el diagrama correspondiente:

(ID 7053)
El flujo laminar alrededor de un cilindro se puede representar como m ltiples capas cil ndricas que se deslizan bajo la influencia de las capas adyacentes. En ese caso, la fuerza viscosa ($F_v$) con el largo de tubo ($\Delta L$), la viscosidad ($\eta$), y las variables la posición radial en cilindro ($r$) y la velocidad en un radio del cilindro ($v$) se expresa como:
| $ F_v =-2 \pi r \Delta L \eta \displaystyle\frac{ dv }{ dr }$ |
La capa en el borde a un radio del tubo ($R$) no se mueve debido al efecto del borde y, a trav s de la viscosidad ($\eta$), ralentiza la capa contigua que s tiene velocidad.
El centro es la parte que se mueve a la velocidad máxima del flujo ($v_{max}$), arrastrando a la capa que lo rodea. A su vez, esta capa arrastra a la siguiente y as sucesivamente hasta llegar a la capa en contacto con la pared del cilindro, que est detenida.

De esta manera, el sistema transfiere energ a desde el centro hasta la pared, generando un perfil de velocidad representado por:
| $ v = v_{max} \left(1-\displaystyle\frac{ r ^2}{ R ^2}\right)$ |
con:
| $ v_{max} =-\displaystyle\frac{ R ^2}{4 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
(ID 7057)
ID:(879, 0)
