User:


Hydraulic element networks
Storyboard

When comparing Darcy's law to Ohm's law in electricity, we notice an analogy where the flow of liquid resembles electric current, the pressure difference relates to the voltage difference, and hydraulic elements are compared to their hydraulic resistances, similar to electric resistors.This analogy implies that, just as there are electrical networks, hydraulic networks can also be defined in which total hydraulic resistances are calculated based on partial hydraulic resistances.

>Model

ID:(1388, 0)


Mechanisms
Concept


ID:(15729, 0)


Hydrodynamic networks
Description

The hydraulic resistance ($R_h$) for an element modeled as a cylindrical tube can be calculated using the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$) through the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



and the hydraulic conductance ($G_h$) can be calculated using:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



which are related by:

$ R_h = \displaystyle\frac{1}{ G_h }$



Both the hydraulic resistance ($R_h$) and the hydraulic conductance ($G_h$) allow for a relationship between the variación de la Presión ($\Delta p$) and the volume flow ($J_V$) using:

$ \Delta p = R_h J_V $



or

$ J_V = G_h \Delta p $

ID:(11098, 0)


Sum of hydraulic resistances in series
Description

In the case of hydraulic resistances connected in series:



the sum of the pressure drop ERROR:10132,0 across each ERROR:9887,0 corresponds to the total pressure difference ($\Delta p_t$):

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



while the total hydraulic resistance in series ($R_{st}$) is described by:

$ R_{st} =\displaystyle\sum_k R_{hk} $



and the total Series Hydraulic Conductance ($G_{st}$) is defined by:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

ID:(15736, 0)


Process for the addition of hydraulic resistances in series
Description

First, values for the hydraulic resistance in a network ($R_{hk}$) are calculated using the variables the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) through the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



These values are then summed to obtain the total hydraulic resistance in series ($R_{st}$):

$ R_{st} =\displaystyle\sum_k R_{hk} $



With this result, it is possible to calculate the volume flow ($J_V$) for the total pressure difference ($\Delta p_t$) using:

$ \Delta p_t = R_{st} J_V $



Once the volume flow ($J_V$) is determined, the pressure difference in a network ($\Delta p_k$) is calculated via:

$ \Delta p_k = R_{hk} J_V $



For the case of three resistances, the calculations can be visualized in the following chart:

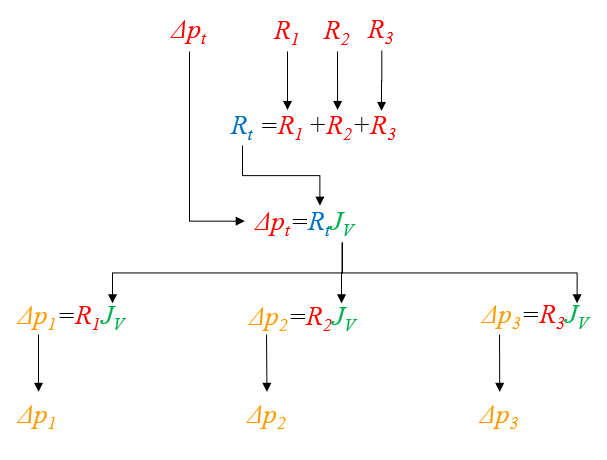
ID:(11069, 0)


Sum of hydraulic resistances in parallel
Description

In the case of hydraulic resistances connected in series:



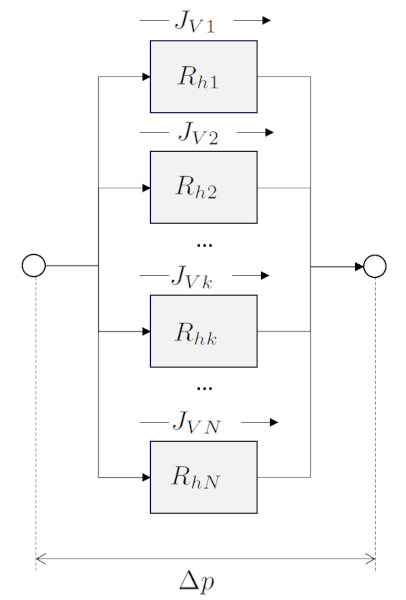
the sum of the pressure drop ERROR:10132,0 across each ERROR:9887,0 corresponds to the total pressure difference ($\Delta p_t$):

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



while the total hydraulic resistance in series ($R_{st}$) is described by:

$ R_{st} =\displaystyle\sum_k R_{hk} $



and the total Series Hydraulic Conductance ($G_{st}$) is defined by:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

ID:(15737, 0)


Process for the addition of hydraulic resistances in parallel
Description

First, values for the hydraulic resistance in a network ($R_{hk}$) are calculated using the variables the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) through the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



These values are then summed to obtain the total hydraulic resistance in series ($R_{st}$):

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$



With this result, it is possible to calculate the variación de la Presión ($\Delta p$) for the total hydraulic resistance in parallel ($R_{pt}$) using:

$ \Delta p = R_{pt} J_{Vt} $



Once the variación de la Presión ($\Delta p$) is determined, the volume flow in a network ($J_{Vk}$) is calculated via:

$ \Delta p = R_{hk} J_{Vk} $



For the case of three resistances, the calculations can be visualized in the following chart:

ID:(11070, 0)


Model
Concept


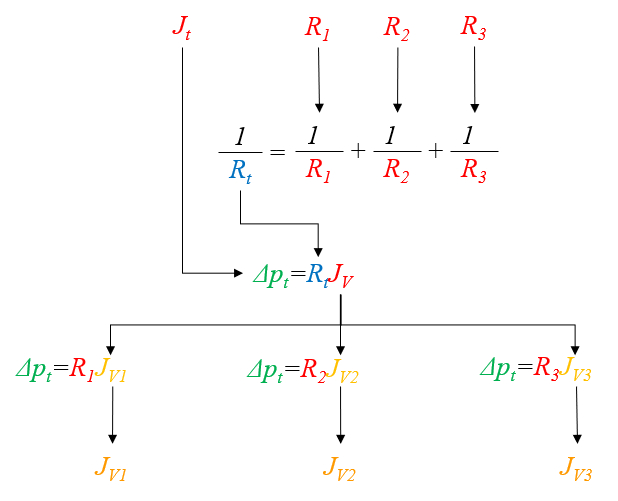
ID:(15734, 0)


Hydraulic element networks
Model

When comparing Darcy's law to Ohm's law in electricity, we notice an analogy where the flow of liquid resembles electric current, the pressure difference relates to the voltage difference, and hydraulic elements are compared to their hydraulic resistances, similar to electric resistors. This analogy implies that, just as there are electrical networks, hydraulic networks can also be defined in which total hydraulic resistances are calculated based on partial hydraulic resistances.

Variables
Symbol
Text
Variable
Value
Units
Calculate
MKS Value
MKS Units
$J_{Vt}$
J_Vt
Flujo de Volumen Total
m^3/s
$G_h$
G_h
Hydraulic conductance
m^4s/kg
$G_{hk}$
G_hk
Hydraulic conductance in a network
m^4s/kg
$R_h$
R_h
Hydraulic resistance
kg/m^4s
$R_{hk}$
R_hk
Hydraulic resistance in a network
kg/m^4s
$G_{pt}$
G_pt
Parallel total hydraulic conductance
m^4s/kg
$\Delta p_k$
Dp_k
Pressure difference in a network
Pa
$R_{pt}$
R_pt
Total hydraulic resistance in parallel
kg/m^4s
$R_{st}$
R_st
Total hydraulic resistance in series
kg/m^4s
$\Delta p_t$
Dp_t
Total pressure difference
Pa
$G_{st}$
G_st
Total Series Hydraulic Conductance
m^4s/kg
$\Delta L$
DL
Tube length
m
$R$
R
Tube radius
m
$\Delta p$
Dp
Variación de la Presión
Pa
$\eta$
eta
Viscosity
Pa s
$J_V$
J_V
Volume flow
m^3/s
$J_{Vk}$
J_Vk
Volume flow in a network
m^3/s

Calculations

First, select the equation:   to ,  then, select the variable:   to 
Symbol
Equation
Solved
Translated

Calculations

Symbol
Equation
Solved
Translated

 Variable   Given   Calculate   Target :   Equation   To be used


Equations

The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:

$ J_V = G_h \Delta p $



Furthermore, using the relationship for the hydraulic resistance ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



results in:

$ \Delta p = R_h J_V $

(ID 3179)

The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:

$ J_V = G_h \Delta p $



Furthermore, using the relationship for the hydraulic resistance ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



results in:

$ \Delta p = R_h J_V $

(ID 3179)

The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:

$ J_V = G_h \Delta p $



Furthermore, using the relationship for the hydraulic resistance ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



results in:

$ \Delta p = R_h J_V $

(ID 3179)

The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:

$ J_V = G_h \Delta p $



Furthermore, using the relationship for the hydraulic resistance ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



results in:

$ \Delta p = R_h J_V $

(ID 3179)

The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:

$ J_V = G_h \Delta p $



Furthermore, using the relationship for the hydraulic resistance ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



results in:

$ \Delta p = R_h J_V $

(ID 3179)

One way to model a tube with varying cross-section is to divide it into sections with constant radius and then sum the hydraulic resistances in series. Suppose we have a series of the hydraulic resistance in a network ($R_{hk}$), which depends on the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) via the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



In each segment, there will be a pressure difference in a network ($\Delta p_k$) with the hydraulic resistance in a network ($R_{hk}$) and the volume flow ($J_V$) to which Darcy's Law is applied:

$ \Delta p_k = R_{hk} J_V $



the total pressure difference ($\Delta p_t$) will be equal to the sum of the individual ERROR:10132,0:

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



therefore,

$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$



Thus, the system can be modeled as a single conduit with the hydraulic resistance calculated as the sum of the individual components:

$ R_{st} =\displaystyle\sum_k R_{hk} $

(ID 3180)

The parallel total hydraulic conductance ($G_{pt}$) combined with the hydraulic conductance in a network ($G_{hk}$) in

$ G_{pt} =\displaystyle\sum_k G_{hk} $



and along with the hydraulic resistance in a network ($R_{hk}$) and the equation

$ R_{st} = \displaystyle\frac{1}{ G_{st} }$



leads to the total hydraulic resistance in parallel ($R_{pt}$) via

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

(ID 3181)

Since the hydraulic resistance ($R_h$) is equal to the hydraulic conductance ($G_h$) as per the following equation:

$ R_h = \displaystyle\frac{1}{ G_h }$



and since the hydraulic conductance ($G_h$) is expressed in terms of the viscosity ($\eta$), the tube radius ($R$), and the tube length ($\Delta L$) as follows:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



we can conclude that:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$

(ID 3629)

The total hydraulic resistance in series ($R_{st}$), along with the hydraulic resistance in a network ($R_{hk}$), in

$ R_{st} =\displaystyle\sum_k R_{hk} $



and along with the hydraulic conductance in a network ($G_{hk}$) and the equation

$ R_{st} = \displaystyle\frac{1}{ G_{st} }$



leads to the total Series Hydraulic Conductance ($G_{st}$) can be calculated with:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 3633)

With the total flow ($J_{Vt}$) being equal to the volume flow in a network ($J_{Vk}$):

$ J_{Vt} =\displaystyle\sum_k J_{Vk} $



and with the pressure difference ($\Delta p$) and the hydraulic conductance in a network ($G_{hk}$), along with the equation

$ J_V = G_h \Delta p $



for each element, it leads us to the conclusion that with the parallel total hydraulic conductance ($G_{pt}$),

$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$



we have

$ G_{pt} =\displaystyle\sum_k G_{hk} $

.

(ID 3634)

If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):

$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$



we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



to arrive at:

$ J_V = G_h \Delta p $

(ID 14471)

Examples


(ID 15729)

The hydraulic resistance ($R_h$) for an element modeled as a cylindrical tube can be calculated using the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$) through the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



and the hydraulic conductance ($G_h$) can be calculated using:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



which are related by:

$ R_h = \displaystyle\frac{1}{ G_h }$



Both the hydraulic resistance ($R_h$) and the hydraulic conductance ($G_h$) allow for a relationship between the variación de la Presión ($\Delta p$) and the volume flow ($J_V$) using:

$ \Delta p = R_h J_V $



or

$ J_V = G_h \Delta p $

(ID 11098)

In the case of hydraulic resistances connected in series:



the sum of the pressure drop ERROR:10132,0 across each ERROR:9887,0 corresponds to the total pressure difference ($\Delta p_t$):

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



while the total hydraulic resistance in series ($R_{st}$) is described by:

$ R_{st} =\displaystyle\sum_k R_{hk} $



and the total Series Hydraulic Conductance ($G_{st}$) is defined by:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 15736)

First, values for the hydraulic resistance in a network ($R_{hk}$) are calculated using the variables the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) through the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



These values are then summed to obtain the total hydraulic resistance in series ($R_{st}$):

$ R_{st} =\displaystyle\sum_k R_{hk} $



With this result, it is possible to calculate the volume flow ($J_V$) for the total pressure difference ($\Delta p_t$) using:

$ \Delta p_t = R_{st} J_V $



Once the volume flow ($J_V$) is determined, the pressure difference in a network ($\Delta p_k$) is calculated via:

$ \Delta p_k = R_{hk} J_V $



For the case of three resistances, the calculations can be visualized in the following chart:

(ID 11069)

In the case of hydraulic resistances connected in series:



the sum of the pressure drop ERROR:10132,0 across each ERROR:9887,0 corresponds to the total pressure difference ($\Delta p_t$):

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



while the total hydraulic resistance in series ($R_{st}$) is described by:

$ R_{st} =\displaystyle\sum_k R_{hk} $



and the total Series Hydraulic Conductance ($G_{st}$) is defined by:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 15737)

First, values for the hydraulic resistance in a network ($R_{hk}$) are calculated using the variables the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$) through the following equation:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



These values are then summed to obtain the total hydraulic resistance in series ($R_{st}$):

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$



With this result, it is possible to calculate the variación de la Presión ($\Delta p$) for the total hydraulic resistance in parallel ($R_{pt}$) using:

$ \Delta p = R_{pt} J_{Vt} $



Once the variación de la Presión ($\Delta p$) is determined, the volume flow in a network ($J_{Vk}$) is calculated via:

$ \Delta p = R_{hk} J_{Vk} $



For the case of three resistances, the calculations can be visualized in the following chart:

(ID 11070)


(ID 15734)

ID:(1388, 0)