Componentes del Suelo
Storyboard 
Las tres componentes fundamentales del suelo son la arena, el limo y la arcilla. Mientras que los granos de arena y limo tienen una forma relativamente esférica, la arcilla se asemeja más a pequeñas plaquitas. Además, existe una notable diferencia en sus tamaños: los granos de arena son solo una fracción de milímetro, los granos de limo tienen dimensiones del orden de micrones, y la arcilla consiste en partículas aún más diminutas, de unos pocos micrones.
Esta variación en los tamaños de partículas tiene un impacto significativo en la capacidad del suelo para compactarse. La arcilla, por ejemplo, puede llenar los espacios intersticiales entre los granos de arena y limo, lo que influye en los diferentes grados de compactación que se pueden lograr en el suelo.
ID:(362, 0)
Componentes del Suelo
Storyboard 
Las tres componentes fundamentales del suelo son la arena, el limo y la arcilla. Mientras que los granos de arena y limo tienen una forma relativamente esférica, la arcilla se asemeja más a pequeñas plaquitas. Además, existe una notable diferencia en sus tamaños: los granos de arena son solo una fracción de milímetro, los granos de limo tienen dimensiones del orden de micrones, y la arcilla consiste en partículas aún más diminutas, de unos pocos micrones. Esta variación en los tamaños de partículas tiene un impacto significativo en la capacidad del suelo para compactarse. La arcilla, por ejemplo, puede llenar los espacios intersticiales entre los granos de arena y limo, lo que influye en los diferentes grados de compactación que se pueden lograr en el suelo.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Cuando observamos la superficie del suelo, con frecuencia encontramos algunas bolos, guijarros, piedrecillas, una masa de color marr n que llamamos suelo y algunas plantas.
Sin embargo, si observamos con mayor atenci n, notaremos que el suelo contiene restos de plantas, desde piedras m s peque as hasta granos de arena. Estos restos de plantas descompuestas corresponden a material org nico de menor tama o que a veces se confunde con el suelo circundante.
En resumen, podemos identificar:
• Bolos, guijarros, piedrecillas
• Materia org nica presente en el suelo.
• El propio suelo en s .
En todos os tipos de solo, encontramos pedras grandes, seixos e pequenas pedras distribu dos em v rias profundidades. Da mesma forma, medida que o solo erodido na superf cie, essas pedras tendem a permanecer nela, uma vez que o solo ao seu redor foi lavado por fluxos superficiais de gua.
A concentra o de pedras grandes, seixos e pequenas pedras varia e afeta as propriedades mec nicas e hidrodin micas do solo. Por um lado, as rochas no interior estabilizam o solo, conferindo-lhe maior resist ncia deforma o. Por outro lado, devido falta de porosidade, elas obstruem o fluxo de gua, afetando o transporte de umidade por difus o. Nesse sentido, o papel das pedras deve ser levado em considera o na modelagem do solo.
En los poros del suelo superficial, se encuentra materia org nica que consiste en residuos de plantas y animales, biomasa microbiana, humus y materia exudada por las ra ces.
Dentro de la biomasa microbiana, encontramos microorganismos como bacterias y hongos. Por otro lado, el humus es un material org nico altamente descompuesto que proviene de restos vegetales y microbianos. El humus mejora significativamente la capacidad del suelo para retener nutrientes y agua.
Cuando observamos un corte en el suelo, en la superficie vemos la cobertura vegetal, y debajo encontramos las ra ces que penetran los primeros cent metros del suelo, que contiene materia org nica. Por materia org nica entendemos material en descomposici n, organismos y microorganismos que viven en entornos acuosos, por lo que se encuentran en los poros del suelo donde se encuentra el agua.
Si observamos en las capas inferiores, notamos que la materia org nica comienza a desaparecer y vemos el suelo en s , con sus tres componentes: arena, limo y arcilla, as como rocas. La concentraci n de estas distintas componentes var a, creando diferentes capas con propiedades f sicas y capacidad de absorci n y transporte de agua diversas.
En resumen, en el suelo podemos identificar componentes distintas a la materia org nica y las rocas principales:
• Arena
• Limo
• Arcilla
La arena fina es un tipo de part cula de suelo caracterizada por su tama o relativamente peque o. Se encuentra entre las part culas m s gruesas de arena y las part culas m s finas de limo en t rminos de tama o. Las part culas de arena fina suelen tener un tama o que va desde 0.02 hasta 0.2 mil metros o de 20 a 200 micr metros.
La arena fina se encuentra com nmente en la composici n del suelo y se caracteriza por su capacidad para retener cierta cantidad de humedad mientras permite un drenaje razonable. Puede contribuir a la textura del suelo y afectar su capacidad para soportar el crecimiento de las plantas. El suelo con una mayor proporci n de arena fina tiende a tener buenas propiedades de aireaci n y drenaje.
La composici n qu mica de la arena puede variar seg n su origen y composici n mineral. La arena generalmente est compuesta por varios minerales, siendo el cuarzo uno de los m s comunes. Sin embargo, la composici n qu mica exacta de la arena puede variar ampliamente. Aqu tienes una visi n general de la composici n qu mica de la arena, con rangos aproximados en porcentaje:
• Quarzo ($SiO_2$) 90% - 95% [1]: El di xido de silicio, com nmente conocido como s lice, es el componente principal de la mayor a de las arenas. Puede constituir entre un 60% y un 95% o m s de la composici n de la arena.
• Feldespato ($KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8$) <10% [1]: El feldespato es otro mineral com n en la arena, y su composici n puede variar. El feldespato pot sico (K-feldespato), el feldespato s dico (Na-feldespato) y el feldespato c lcico (Ca-feldespato) son diferentes tipos de minerales de feldespato que se encuentran en la arena.
• Mica (Muscovita, Biotita) <5% [1]: Los minerales de mica, como la muscovita y la biotita, pueden variar entre el 1% y el 5% o menos de la composici n del limo.
• Otros Minerales: Dependiendo de la fuente geol gica de la arena, esta puede contener trazas de otros minerales, como feldespato, mica o magnetita.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
El limo es un tipo de part cula de suelo que se encuentra entre la arena y la arcilla en t rminos de tama o de part cula. Las part culas de limo generalmente tienen un tama o que oscila entre 0.002 y 0.02 mil metros, lo que equivale a 2 a 20 micr metros. Estas part culas son m s peque as que las de arena pero m s grandes que las de arcilla.
Una caracter stica distintiva del limo es su capacidad para retener la humedad y los nutrientes, lo que lo convierte en un suelo adecuado para la agricultura. Sin embargo, es importante tener en cuenta que el limo puede compactarse y presentar problemas de drenaje si predomina en la composici n del suelo. Los suelos con contenido de limo suelen ser f rtiles y pueden sustentar una variedad de cultivos cuando se manejan adecuadamente.
La composici n qu mica del limo puede variar seg n su origen y ubicaci n geogr fica. Sin embargo, en t rminos generales, el limo est compuesto por varios minerales y puede contener materia org nica. A continuaci n, proporciono una aproximaci n de la composici n qu mica del limo en t rminos de los principales elementos, expresados como porcentaje de la composici n total:
• Quarzo ($SiO_2$) 40-60% [1]: El cuarzo suele ser el mineral dominante en el limo, representando aproximadamente entre el 50% y el 70% o incluso m s de su composici n.
• Feldespato ($KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8$) <10% [1]: Los minerales de feldespato, que incluyen feldespato pot sico, feldespato s dico y feldespato c lcico, pueden variar desde un 10% hasta un 30% o m s de la composici n.
• Mica (Muscovita, Biotita) < 5% [1]: Los minerales de mica, como la muscovita y la biotita, pueden variar entre el 1% y el 5% o menos de la composici n del limo.
• Otros Minerales: El limo puede contener trazas de varios otros minerales seg n su origen geol gico espec fico, como circ n, granate y otros.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
La arcilla es un tipo de part cula de suelo con part culas muy finas, t picamente m s peque as de 0.002 mil metros de tama o o menos de 2 micr metros. Las part culas de arcilla son mucho m s peque as que las part culas de arena y limo. Los suelos arcillosos son conocidos por su capacidad para retener agua y nutrientes debido a su peque o tama o de part cula y alta rea superficial. Sin embargo, tambi n pueden compactarse f cilmente y pueden tener propiedades de drenaje deficientes. Los suelos arcillosos pueden variar en color y textura seg n su composici n mineral y contenido de materia org nica. Son un componente importante de muchos tipos de suelos y pueden influir en la fertilidad y estructura del suelo.
La composici n qu mica de la arcilla puede variar seg n su composici n mineral espec fica y su origen. La arcilla est compuesta principalmente por diminutas part culas minerales y generalmente consiste en varios minerales, que incluyen:
• Caolinita ($Al_2Si_2O_5(OH)_4$) 20-40% [1]: La caolinita es un mineral de arcilla com n y el principal componente de la arcilla de caol n.
• Illita ($(K, H_3O)(Al, Mg, Fe)_2(Si, Al)_4O_{10}[(OH)_2,(H_2O)]$) 10-40% [1]: La illita es otro mineral de arcilla com n.
• Esmectitas/Montmorillonita ($(Na, Ca)_{0.33}(Al, Mg)_2(Si_4O_{10})(OH)_2 n(H_2O)$) 10-40% [1]: La montmorillonita es un mineral de arcilla conocido por sus propiedades de hinchamiento.
• Clorita ($(Mg, Fe)_3(Si, Al)_4O_{10}(OH)_2 (Mg, Fe)_3(OH)_6$) <10% [1]: A veces, se encuentra clorita en minerales de arcilla.
• Otros Minerales: Adem s, dependiendo del dep sito de arcilla espec fico, otros minerales tambi n pueden estar presentes en cantidades m nimas, incluyendo cuarzo, feldespato y varios xidos met licos.
[1] Clay Mineralogy, Ralph E. Grim, McGraw-Hill International Series
Para modelar el suelo de manera efectiva, es fundamental considerar las formas geom tricas que mejor describen los diversos tipos de granos que componen el suelo.
Para ello, se deben observar m ltiples granos de cada tipo. En el caso de la arena, esto es posible bajo un microscopio normal y permite obtener colecciones de granos como la que se observa a continuaci n:
En este caso, podemos concluir que la forma es redondeada, por lo que se les puede representar efectivamente como esferas.
Por lo general, los granos de arena y granos de limo son conglomerados de m ltiples cristales que est n expuestos a impactos a medida que son transportados por el agua o el viento. Estos impactos generan fracturas a lo largo de los planos del cristal, eliminando fragmentos sobresalientes y, como resultado, redondeando el grano:
De esta manera, tienden a volverse m s redondeados y adquieren una forma que se asemeja a peque as esferas.
Los granos de arcilla suelen ser peque os cristales que est n expuestos a impactos a medida que son transportados por el agua o el viento. Estos impactos generan fracturas a lo largo de los planos del cristal, lo que, dado que el grano es un cristal, implica que mantenga su forma sin redondear las esquinas:
Por lo tanto, los granos de arcilla se caracterizan por tener una forma geom trica similar a peque as placas que se asemejan a paralelep pedos rectos.
Si observamos los granos bajo un microscopio, notaremos que tienen formas relativamente redondeadas y tama os variables, aunque tienden a ser de un tama o similar:
Por lo tanto, en una primera aproximaci n, los granos pueden ser modelados como esferas:
Los granos de arena pueden modelarse como esferas. Para simplificar el modelo, se asume que todos son iguales. Sin embargo, un modelo m s detallado podr a considerar la distribuci n de radios diversos.
En l nea con la hip tesis inicial de que los granos de arena se pueden modelar como esferas, se puede introducir su correspondiente radio.
Por lo tanto, introducimos el radio el radio del grano de arena ($r_a$) para describir las esferas de los granos de arena.
Debe tenerse presente que el radio es un valor medio, dado que varia entre los distintos granos.
Si observamos los granos de limo bajo un microscopio, notaremos que tienen formas relativamente cubicas y tama os variables, aunque tienden a ser de un tama o similar:
Por lo tanto, en una primera aproximaci n, los granos pueden ser modelados como cubos:
Los granos de limo pueden modelarse como cubos. Para simplificar el modelo, se asume que todos son iguales. Sin embargo, un modelo m s detallado podr a considerar la distribuci n de lados diversos.
En l nea con la hip tesis inicial de que los granos de limo se pueden modelar como cubos, se puede introducir su correspondiente lado.
Por lo tanto introducimos el lado del cubo el lado del grano de limo ($a_i$) para describir los granos de limo.
Debe tenerse presente que el lado es un valor medio, dado que varia entre los distintos granos.
Los granos de arcilla son relativamente planos y tienden a apilarse en forma paralela, como se puede apreciar en esta imagen obtenida mediante un microscopio electr nico:
Su forma se asemeja a elementos planos de grosor reducido que se parecen a paralelep pedos rectos:
Los granos de arcilla pueden modelarse como paralelep pedos rectos. Para simplificar el modelo, se asume que todos son iguales. Sin embargo, un modelo m s detallado podr a considerar la distribuci n de longitudes y alturas diversas.
En l nea con la hip tesis inicial de que los granos de arcilla se pueden modelar como paralelep pedos rectos, se pueden introducir sus correspondientes longitudes y altura.
Por lo tanto se introduce para describir el paralelepipedo recto el largo y ancho de una plaquita de arcilla ($l_c$) y la altura de una plaquita de arcilla ($w_c$).
Debe tenerse presente que las longitudes y la altura son valores medios, dado que en realidad var an entre los distintos granos.
Para calcular la masa de un grano de arena, es esencial conocer su densidad. Sin embargo, es importante destacar que la densidad del grano en s difiere significativamente de la densidad de la arena en su conjunto, debido a la presencia de una alta porosidad en esta ltima. Por lo tanto, para estimar la densidad de un grano de arena, se debe analizar la densidad de sus minerales principales, que se detallan a continuaci n:
| Mineral | Ocurrencia | Densidad [$g/cm^3$] |
| Quarzo | 90-95% [1] | 2.65 [2] |
| Feldspars | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Para desarrollar un modelo simple, se puede asumir una densidad homog nea:
Si suponemos que los minerales de los que est n compuestos los granos de arena est n distribuidos de manera homog nea, podemos asumir que los granos tienen una densidad constante y uniforme en todos ellos.
Con ello se introduce la densidad de un grano de arena ($\rho_a$).
Es importante tener presente que valor puede variar seg n la composici n de los granos de arena.
Para calcular la masa de un grano de limo, es esencial conocer su densidad. Sin embargo, es importante destacar que la densidad del grano en s difiere significativamente de la densidad del limo en su conjunto, debido a la presencia de una alta porosidad en esta ltima. Por lo tanto, para estimar la densidad de un grano de limo, se debe analizar la densidad de sus minerales principales, que se detallan a continuaci n:
| Mineral | Ocurrencia | Densidad [$g/cm^3$] |
| Quarzo | 40-60% [1] | 2.65 [2] |
| Feldspars | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Para desarrollar un modelo simple, se puede asumir una densidad homog nea:
Si suponemos que los minerales de los que est n compuestos los granos de limo est n distribuidos de manera homog nea, podemos asumir que los granos tienen una densidad constante y uniforme en todos ellos.
Con ello se introduce la densidad de un grano de limo ($\rho_i$).
Es importante tener presente que valor puede variar seg n la composici n de los granos de limo.
Para calcular la masa de un grano de arcilla, resulta fundamental conocer su densidad. No obstante, es crucial destacar que la densidad del grano en s difiere significativamente de la densidad de arcilla en su totalidad, debido a la notable presencia de una alta porosidad en esta ltima. Por lo tanto, para estimar la densidad de un grano de arcilla, es necesario analizar la densidad de sus minerales principales, que se describen a continuaci n:
| Mineral | Ocurrencia | Densidad [$g/cm^3$] |
| Esmectitas | 0-80% [1] | 2.75-2.78 [2] |
| Illitas | 10-80% [1] | 2.60-2.86 [2] |
| Caolinitas | 20-80% [1] | 2.62-2.66 [2] |
| Cloritas | 0-30% [1] | 2.60-2.96 [2] |
[1] Clay Mineralogy, Ralph E. Grim (1968), McGraw-Hill
[2] Geotechnical Engineering Principles and Practices, Donald P. Coduto et al. (1998), Prentice-Hall
Para desarrollar un modelo simple, se puede asumir una densidad homog nea:
Si suponemos que los minerales de los que est n compuestos los granos de arcilla est n distribuidos de manera homog nea, podemos asumir que los granos tienen una densidad constante y uniforme en todos ellos.
Con ello se introduce la densidad de un grano de arcilla ($\rho_c$).
Es importante tener presente que este valor puede variar seg n la composici n espec fica de los granos de arcilla.
El estudio de los granos en una muestra de suelo implica un an lisis exhaustivo de varios aspectos que contribuyen a comprender las propiedades f sicas y el comportamiento del suelo. A continuaci n, se presenta una explicaci n detallada de los componentes clave de este estudio:
T rminos de Tama o:
- Los t rminos de tama o se refieren a la categorizaci n de las part culas de suelo seg n su di metro. Las part culas de suelo suelen clasificarse en tres categor as principales:
Arena: Las part culas m s grandes, con di metros que van desde 0.05 mm hasta 2 mm.
Limo: Part culas de tama o intermedio, que van desde 0.002 mm hasta 0.05 mm.
Arcilla: Las part culas m s peque as, con di metros inferiores a 0.002 mm.
- Las proporciones relativas de estas fracciones de tama o determinan la textura del suelo, lo que, a su vez, afecta sus propiedades, como la retenci n de agua y el drenaje.
Tama os de Tamices:
- Los tama os de tamices son tama os de malla estandarizados utilizados para separar las part culas de suelo por tama o. Los tama os comunes de tamices est n definidos por los est ndares ASTM (Sociedad Estadounidense de Pruebas y Materiales) o ISO (Organizaci n Internacional de Normalizaci n).
- El an lisis de tamices implica pasar una muestra de suelo a trav s de un conjunto de tamices con mallas progresivamente m s finas para determinar la distribuci n del tama o de las part culas.
N mero de Granos por mg:
- Esta m trica representa la densidad de part culas de suelo dentro de una masa dada de suelo. Se calcula contando el n mero de part culas dentro de una masa conocida de suelo (generalmente 1 mg) y luego extrapolando para estimar el n mero total de part culas en una muestra m s grande.
- Proporciona informaci n sobre la poblaci n y el espaciado de las part culas de suelo, lo que puede ser esencial para comprender la compactaci n del suelo y la penetraci n de las ra ces.
Velocidad de Sedimentaci n:
- La velocidad de sedimentaci n se refiere a la velocidad a la que las part culas de suelo caen a trav s de un fluido (generalmente agua) bajo la influencia de la gravedad. Esta velocidad est determinada por el tama o, la forma y la densidad de las part culas y la viscosidad del fluido.
- El conocimiento de las velocidades de sedimentaci n es valioso en estudios de sedimentaci n y puede ayudar a predecir cu nto tiempo lleva que las part culas se sedimenten fuera de la suspensi n en cuerpos de agua.
Velocidad Umbral para la Tracci n:
- La velocidad umbral para la tracci n representa la velocidad m nima del flujo de agua necesaria para iniciar el movimiento de part culas de suelo en el lecho de un arroyo o r o. Es un par metro importante en estudios de transporte de sedimentos.
- Cuando la velocidad del agua supera la velocidad umbral para un tama o de part cula espec fico, puede erosionar y transportar esas part culas, lo que puede tener importantes implicaciones ambientales.
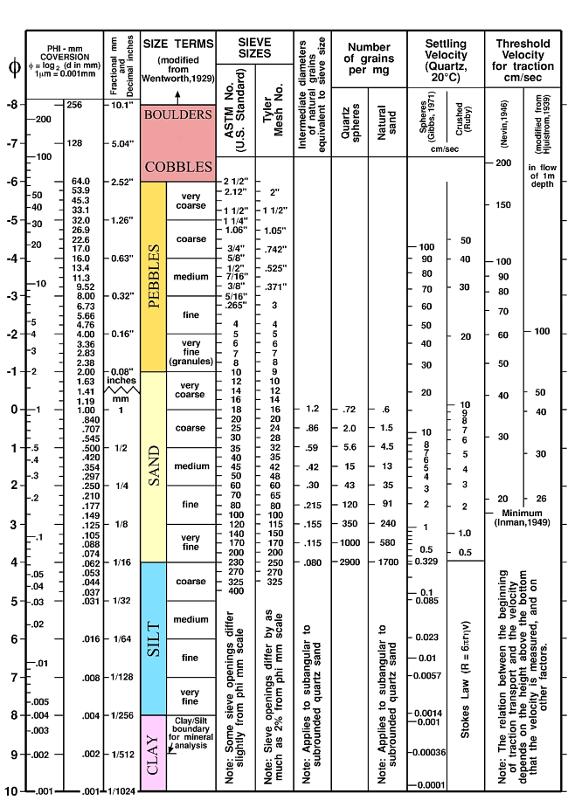
A modo de ejemplo, aqu se muestra la tabla de tama os de part culas medida en el Long Island Sound por la Oficina Geol gica de los Estados Unidos (USGS).
El modelo se puede definir considerando tres tipos de materiales (arena, limo y arcilla), con granos modelados de la siguiente manera: en los dos primeros casos, los granos se representan como esferas con radios de diferentes tama os, mientras que en el caso de la arcilla, los granos se modelan como paralelep pedos rectos.
Los rangos de los par metros se resumen en la siguiente tabla:
| Tipo | Par metro | S mbolo | Rango | Unidad |
| Arena | Radio | $r_a$ | 62 - 2000 | $\mu m$ |
| Volumen | $v_a$ | 1 - 33500 | $nl$ | |
| Densidad | $\rho_a$ | 2.64 - 2.69 | $g/cm^3$ | |
| Masa | $m_a$ | 2.6 - 90100 | $\mu g$ | |
| Limo | Radio | $r_i$ | 4 - 62 | $\mu m$ |
| Volumen | $v_i$ | 0.27 - 990 | $pl$ | |
| Densidad | $\rho_i$ | 2.63 - 2.72 | $g/cm^3$ | |
| Masa | $m_i$ | 0.71 - 2700 | $ng$ | |
| Arcilla | Largo | $l_c$ | 1 - 4 | $\mu m$ |
| Altura | $w_c$ | 0.1 - 0.4 | $\mu m$ | |
| Volumen | $v_c$ | 0.1 - 6.4 | $fl$ | |
| Densidad | $\rho_c$ | 2.66 - 2.80 | $g/cm^3$ | |
| Masa | $m_c$ | 0.27 - 17.9 | $pg$ |
Al ser tan peque os los granos se hace necesario trabajar en un gran rango de las dimensiones. Por ello se emplean las abreviaviaciones:
Largos
| S mbolo | Unidad | MKS |
| $m$ | metro | $1 m$ |
| $mm$ | milimetro | $10^{-3} m$ |
| $\mu m$ | micrometro | $10^{-6} m$ |
Volumen
| S mbolo | Unidad | MKS |
| $m^3$ | metro cubico | $1 m^3$ |
| $l$ | litro | $10^{-3} m^3$ |
| $ml$ | mililitro | $10^{-6} m^3$ |
| $\mu l$ | microlitro | $10^{-9} m^3$ |
| $nl$ | nanolitro | $10^{-12} m^3$ |
| $pl$ | picolitro | $10^{-15} m^3$ |
| $fl$ | fentolitro | $10^{-18} m^3$ |
Masa
| S mbolo | Unidad | MKS |
| $kg$ | kilogramo | $1 kg$ |
| $g$ | gramo | $10^{-3} kg$ |
| $mg$ | miligramo | $10^{-6} kg$ |
| $\mu g$ | microgramo | $10^{-9} kg$ |
| $ng$ | nanogramo | $10^{-12} kg$ |
| $pg$ | picogramo | $10^{-15} kg$ |
Densidad
| S mbolo | Unidad | MKS |
| $kg/m^3$ | kilogramo por metro cubico | $1 kg/m^3$ |
| $g/cm^3$ | gramo por centimetro cubico | $10^{3} kg/m^3$ |
Si modelamos un grano de arena como una esfera y asumimos que el radio del grano de arena ($r_a$), podemos calcular su el volumen de un grano de arena ($v_a$) utilizando la siguiente ecuaci n:
Sin embargo, es importante tener en cuenta que este c lculo proporciona un valor estimado del volumen, ya que el radio es un valor promedio. Para obtener un c lculo m s preciso e incluso determinar un volumen promedio, ser a necesario estudiar la distribuci n de los radios de los granos de arena en el estudio.
Es relevante destacar que el volumen calculado es solo un valor de referencia, ya que se basa en la suposici n de que la arena est compuesta por esferas perfectas e id nticas, lo cual no es el caso en la realidad.
Si modelamos un grano de limo como un paralelepipedo recto y asumimos que el lado del grano de limo ($a_i$), podemos calcular su el volumen de un grano de limo ($v_i$) utilizando la siguiente ecuaci n:
Sin embargo, es importante destacar que este c lculo proporciona un valor estimado del volumen, ya que el lado es un valor promedio. Para obtener un c lculo m s preciso e incluso determinar un volumen promedio, ser a necesario estudiar la distribuci n de los lados de los granos de limo en el estudio.
Es relevante enfatizar que el volumen calculado sirve como un valor de referencia, ya que se basa en la suposici n de que el limo est compuesto por cubos perfectas e id nticas, lo cual no es el caso en la realidad.
Si modelamos un grano de arcilla como un paralelep pedo recto y asumimos que tiene el largo y ancho de una plaquita de arcilla ($l_c$) y la altura de una plaquita de arcilla ($w_c$), podemos calcular el volumen de un grano de arcilla ($v_c$) mediante:
Sin embargo, es importante tener en cuenta que este c lculo proporciona un valor estimado del volumen, ya que los lados y la altura son valores promedio. Para obtener un c lculo m s preciso e incluso determinar un volumen promedio, ser a necesario estudiar la distribuci n de los lados y alturas de los granos de arcilla en el estudio.
Es relevante destacar que el volumen calculado es solo un valor de referencia, ya que se basa en la suposici n de que la arcilla est compuesta por paralelepipedos rectos perfectas e id nticas, lo cual no es el caso en la realidad.
Una vez que disponemos de el volumen de un grano de arena ($v_a$) y la densidad de un grano de arena ($\rho_a$), podemos determinar la masa de un grano de arena ($m_a$) mediante la siguiente ecuaci n:
Sin embargo, es importante tener en cuenta que tanto el volumen como la densidad del grano de arena son estimaciones, por lo que la masa resultante es principalmente un valor de referencia. Para realizar un c lculo m s preciso, ser a necesario analizar la distribuci n de las formas y composiciones mineral gicas para obtener un valor medio m s exacto.
Es fundamental destacar que la masa calculada se utiliza como punto de referencia, ya que se basa en la suposici n de que la arena est compuesta por esferas perfectas y que las densidades de los granos son id nticas, lo cual no es el caso en la realidad.
Una vez que disponemos de el volumen de un grano de limo ($v_i$) y la densidad de un grano de limo ($\rho_i$), podemos determinar la masa de un grano de limo ($m_i$) mediante la siguiente ecuaci n:
Sin embargo, es fundamental recordar que tanto el volumen como la densidad del grano de limo son estimaciones, por lo que la masa resultante es un valor de referencia. Para obtener un c lculo m s preciso, ser a necesario estudiar la distribuci n de las formas y composiciones mineral gicas para obtener un valor medio m s exacto.
Es relevante subrayar que la masa calculada sirve como un punto de referencia, ya que se basa en la suposici n de que el limo est compuesto por esferas perfectas y que las densidades de los granos son id nticas, lo cual no es el caso en la realidad.
Una vez que disponemos de el volumen de un grano de arcilla ($v_c$) y la densidad de un grano de arcilla ($\rho_c$), podemos determinar la masa de una plaquita de arcilla ($m_c$) mediante la siguiente ecuaci n:
Sin embargo, es fundamental recordar que tanto el volumen como la densidad del grano de arcilla son estimaciones, por lo que la masa resultante es un valor de referencia. Para obtener un c lculo m s preciso, ser a necesario estudiar la distribuci n de las formas y composiciones mineral gicas para obtener un valor medio m s exacto.
Es relevante subrayar que la masa calculada sirve como un punto de referencia, ya que se basa en la suposici n de que la arcilla est compuesta por paralelep pedos perfectos y que las densidades de los granos son id nticas, lo cual no es el caso en la realidad.
ID:(362, 0)