Usuario:


Flujo por múltiples Capas
Storyboard

Una vez calculada la resistencia hidráulica y la conductividad, es posible modelar un sistema de suelo con múltiples capas. Para lograrlo, es necesario calcular la resistencia y la conductividad totales, y después de establecer el flujo global, determinar los flujos parciales (en el caso de capas paralelas) o la caída de presión en cada capa (en el caso de capas en serie).

>Modelo

ID:(371, 0)


Flujo por múltiples Capas
Descripción

Una vez calculada la resistencia hidráulica y la conductividad, es posible modelar un sistema de suelo con múltiples capas. Para lograrlo, es necesario calcular la resistencia y la conductividad totales, y después de establecer el flujo global, determinar los flujos parciales (en el caso de capas paralelas) o la caída de presión en cada capa (en el caso de capas en serie).

Variables
Símbolo
Texto
Variable
Valor
Unidades
Calcule
Valor MKS
Unidades MKS
$H$
H
Altura de la capa
m
$G_h$
G_h
Conductancia hidráulica
m^4s/kg
$G_{hk}$
G_hk
Conductancia hidráulica en una red
m^4s/kg
$G_{pt}$
G_pt
Conductancia hidráulica total en paralelo
m^4s/kg
$G_{st}$
G_st
Conductancia hidráulica total en serie
m^4s/kg
$\rho_b$
rho_b
Densidad aparente seca
kg/m^3
$\rho_s$
rho_s
Densidad sólida
kg/m^3
$\Delta p_k$
Dp_k
Diferencia de presión en una red
Pa
$\Delta p_t$
Dp_t
Diferencia de presión total
Pa
$\Delta p$
Dp
Diferencial de la presión
Pa
$d$
d
Distancia Horizontal
m
$\theta_c$
theta_c
Factor de relación porosidad-arcilla
-
$J_V$
J_V
Flujo de volumen
m^3/s
$J_{V1}$
J_V1
Flujo de volumen 1
m^3/s
$J_{V2}$
J_V2
Flujo de volumen 2
m^3/s
$J_{Vk}$
J_Vk
Flujo de volumen en una red
m^3/s
$J_{Vt}$
J_Vt
Flujo de volumen total
m^3/s
$g_a$
g_a
Fracción de masa de arena en la muestra
-
$h$
h
Incremento de altura
m
$d_2$
d_2
Media altura de la capa
m
$m$
m
Pendiente
-
$f$
f
Porosidad
-
$R_h$
R_h
Resistencia hidráulica
kg/m^4s
$R_{hk}$
R_hk
Resistencia hidráulica en una red
kg/m^4s
$R_{pt}$
R_pt
Resistencia hidráulica total en paralelo
kg/m^4s
$R_{st}$
R_st
Resistencia hidráulica total en serie
kg/m^4s
$S_1$
S_1
Sección en el punto 1
m^2
$S_2$
S_2
Sección en el punto 2
m^2
$S$
S
Sección o superficie
m^2
$V_p$
V_p
Volumen de los poros
m^3
$V_c$
V_c
Volumen sólido de arcilla
m^3

Cálculos

Primero, seleccione la ecuación:   a ,  luego, seleccione la variable:   a 
Símbolo
Ecuación
Resuelto
Traducido

Cálculos

Símbolo
Ecuación
Resuelto
Traducido

 Variable   Dado   Calcule   Objetivo :   Ecuación   A utilizar


Ecuaciones

El flujo de volumen ($J_V$) se puede determinar a partir de la conductancia hidráulica ($G_h$) y la diferencia de presión ($\Delta p$) utilizando la ecuaci n siguiente:

$ J_V = G_h \Delta p $



Adem s, utilizando la relaci n para la resistencia hidráulica ($R_h$):

$ R_h = \displaystyle\frac{1}{ G_h }$



se obtiene el resultado final:

$ \Delta p = R_h J_V $

(ID 3179)

Una forma de modelar un tubo en el que var a la secci n es dividirlo en secciones de radio constante y luego sumar las resistencias hidr ulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la siguiente ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



En cada elemento habr una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy

$ \Delta p = R_h J_V $



la diferencia de presión total ($\Delta p_t$) ser igual a la suma de las ERROR:10132,0 individuales

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



por lo que

$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$



Por lo tanto, el sistema se puede modelar como un conducto nico con la resistencia hidr ulica calculada como la suma de las componentes individuales:

$ R_{st} =\displaystyle\sum_k R_{hk} $

(ID 3180)

La conductancia hidráulica total en paralelo ($G_{pt}$) junto con la conductancia hidráulica en una red ($G_{hk}$) en

$ G_{pt} =\displaystyle\sum_k G_{hk} $



y junto con la resistencia hidráulica en una red ($R_{hk}$) y la ecuaci n

$ R_h = \displaystyle\frac{1}{ G_h }$



conduce a la resistencia hidráulica total en paralelo ($R_{pt}$) mediante

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

(ID 3181)

La resistencia hidráulica total en serie ($R_{st}$), junto con la resistencia hidráulica en una red ($R_{hk}$) en

$ R_{st} =\displaystyle\sum_k R_{hk} $



y junto con la conductancia hidráulica en una red ($G_{hk}$) y la ecuaci n

$ R_h = \displaystyle\frac{1}{ G_h }$



conduce a que la conductancia hidráulica total en serie ($G_{st}$) se puede calcular con:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 3633)

Con el flujo total ($J_{Vt}$) siendo igual a el flujo de volumen en una red ($J_{Vk}$):

$ J_{Vt} =\displaystyle\sum_k J_{Vk} $



y con la diferencia de presión ($\Delta p$) y la conductancia hidráulica en una red ($G_{hk}$), junto con la ecuaci n

$ J_V = G_h \Delta p $



para cada elemento, podemos deducir que, con la conductancia hidráulica total en paralelo ($G_{pt}$),

$J_{Vt}=\displaystyle\sum_k J_{Vk} = \displaystyle\sum_k G_{hk}\Delta p = G_{pt}\Delta p$



lo que implica que

$ G_{pt} =\displaystyle\sum_k G_{hk} $

.

(ID 3634)

Dado que la densidad de flujo ($j_s$) est relacionado con el radio de un grano genérico ($r_0$), la porosidad ($f$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$), la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), la diferencia de altura ($\Delta h$) y el largo de la muestra ($\Delta L$) a trav s de la ecuaci n

$ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$



Podemos definir un factor al que llamaremos la conductividad hidráulica ($K_s$) de la siguiente manera:

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$

Este factor incorpora todos los elementos relacionados con las propiedades del suelo y del l quido que fluye a trav s de l.

(ID 4739)

Como la resistencia hidráulica ($R_h$) est relacionado con la conductividad hidráulica ($K_s$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$), la sección de la columna ($S$) y el largo de la muestra ($\Delta L$), se expresa como

$ R_h = \displaystyle\frac{ \rho_w g }{ K_s }\displaystyle\frac{ \Delta L }{ S }$



Y la relaci n para la conductancia hidráulica ($G_h$)

$ R_h = \displaystyle\frac{1}{ G_h }$



lleva a

$ G_h = \displaystyle\frac{ K_s }{ \rho_w g }\displaystyle\frac{ S }{ \Delta L }$

(ID 10592)

Usando la Ley de Darcy, donde la diferencia de presión ($\Delta p$) se iguala a la resistencia hidráulica ($R_h$) y el flujo total ($J_{Vt}$):

$ \Delta p = R_h J_V $



As , con la ecuaci n para el suelo con la sección del flujo ($S$), el radio de un grano genérico ($r_0$), la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), la porosidad ($f$), la diferencia de presión ($\Delta p$) y el largo de la muestra ($\Delta L$):

$ J_{Vt} =-\displaystyle\frac{ r_0 ^2}{8 \eta q_0 }\displaystyle\frac{ f ^3}{(1- f )^2}\displaystyle\frac{ S }{ \Delta L } \Delta p $



Entonces, la resistencia hidráulica ($R_h$) es:

$ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$

(ID 10594)

Calculando la resistencia hidráulica ($R_h$) utilizando la viscosidad ($\eta$), la porosidad propia genérica ($q_0$), el radio de un grano genérico ($r_0$), la porosidad ($f$), el largo de la muestra ($\Delta L$) y la sección de la columna ($S$) a trav s de

$ R_h = \displaystyle\frac{8 \eta q_0 }{ r_0 ^2}\displaystyle\frac{(1- f )^2 }{f ^3}\displaystyle\frac{ \Delta L }{ S }$



y utilizando la expresi n para la conductividad hidráulica ($K_s$)

$ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$



se obtiene despu s de reemplazar los factores comunes

$ R_h = \displaystyle\frac{ \rho_w g }{ K_s }\displaystyle\frac{ \Delta L }{ S }$

(ID 10635)

Si observamos la ley de Hagen-Poiseuille, que nos permite calcular el flujo de volumen ($J_V$) a partir de el radio del tubo ($R$), la viscosidad ($\eta$), el largo de tubo ($\Delta L$) y la diferencia de presión ($\Delta p$):

$ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$



podemos introducir la conductancia hidráulica ($G_h$) definido en t rminos de el largo de tubo ($\Delta L$), el radio del tubo ($R$) y la viscosidad ($\eta$) de la siguiente manera:

$ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$



y as obtener:

$ J_V = G_h \Delta p $

(ID 14471)

Ejemplos


(ID 15204)

En el caso de una suma en la que los elementos est n conectados en serie, la resistencia hidr ulica total del sistema se calcula sumando las resistencias individuales de cada elemento.



Una forma de modelar un tubo en el que var a la secci n es dividirlo en secciones de radio constante y luego sumar las resistencias hidr ulicas en serie. Supongamos que tenemos una serie de la resistencia hidráulica en una red ($R_{hk}$), que depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$) a trav s de la siguiente ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



En cada elemento habr una diferencia de presión en una red ($\Delta p_k$) con la resistencia hidráulica en una red ($R_{hk}$) y el flujo de volumen ($J_V$) para los que se aplica la ley de Darcy

$ \Delta p = R_h J_V $



la diferencia de presión total ($\Delta p_t$) ser igual a la suma de las ERROR:10132,0 individuales

$ \Delta p_t =\displaystyle\sum_k \Delta p_k $



por lo que

$\Delta p_t=\displaystyle\sum_k \Delta p_k=\displaystyle\sum_k (R_{hk}J_V)=\left(\displaystyle\sum_k R_{hk}\right)J_V\equiv R_{st}J_V$



Por lo tanto, el sistema se puede modelar como un conducto nico con la resistencia hidr ulica calculada como la suma de las componentes individuales:

$ R_{st} =\displaystyle\sum_k R_{hk} $

(ID 3630)

En el caso de una suma en la que los elementos est n conectados en serie, la conductancia hidr ulica total del sistema se calcula sumando las conductancias individuales de cada elemento.



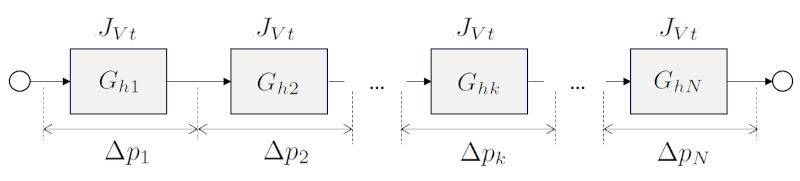
la resistencia hidráulica total en serie ($R_{st}$), junto con la resistencia hidráulica en una red ($R_{hk}$) en

$ R_{st} =\displaystyle\sum_k R_{hk} $



y junto con la conductancia hidráulica en una red ($G_{hk}$) y la ecuaci n

$ R_h = \displaystyle\frac{1}{ G_h }$



conduce a que la conductancia hidráulica total en serie ($G_{st}$) se puede calcular con:

$\displaystyle\frac{1}{ G_{st} }=\displaystyle\sum_k\displaystyle\frac{1}{ G_{hk} }$

(ID 11067)

Una situaci n en el suelo en la que los elementos est n conectados en serie es cuando el agua se filtra verticalmente a trav s de varias capas para finalmente terminar en la napa fre tica. En este caso, la sección de la columna ($S$) es constante, mientras que cada capa tiene un ancho distinto que act a como la ancho de la k-esima capa ($L_k$).



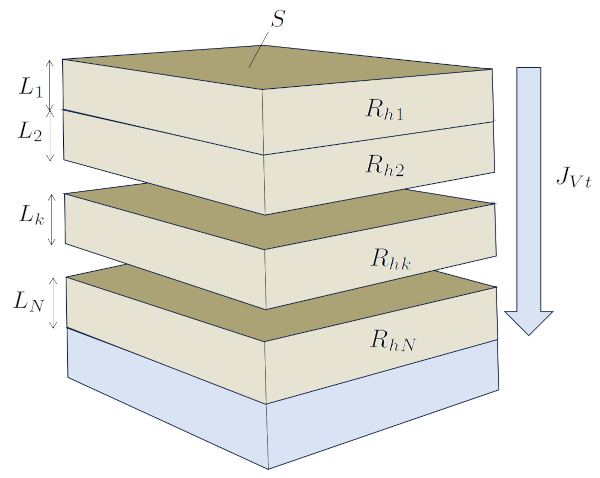
En esta situaci n, las resistencias hidr ulicas se suman directamente, y sus valores dependen del tipo de suelo, y por lo tanto, de la conductividad hidráulica en la k-esima capa ($K_{sk}$) y de la ancho de la k-esima capa ($L_k$).

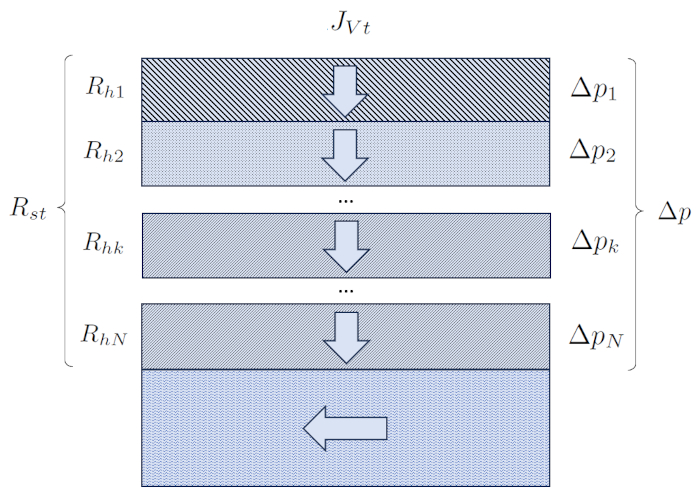
(ID 936)

Una forma eficiente de modelar un tubo de secci n variable es dividirlo en m ltiples secciones con radios constantes, sumando posteriormente las resistencias hidr ulicas de cada secci n en serie. Consideremos que tenemos una serie de elementos la resistencia hidráulica en una red ($R_{hk}$), cuya resistencia depende de la viscosidad ($\eta$), el radio del cilindro k ($R_k$) y el largo de tubo k ($\Delta L_k$), de acuerdo con la siguiente ecuaci n:

$ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$



En cada elemento se considera una diferencia de presión en una red ($\Delta p_k$) junto con la resistencia hidráulica en una red ($R_{hk}$) y el caudal volum trico el flujo de volumen ($J_V$), aplicando la ley de Darcy a cada uno de ellos:

$ \Delta p = R_h J_V $



La resistencia total del sistema, el flujo de volumen total ($J_{Vt}$), ser la suma de las resistencias hidr ulicas individuales ERROR:10133,0 de cada secci n:

$ J_{Vt} =\displaystyle\sum_k J_{Vk} $



Por lo tanto, tenemos:

$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$



De esta forma, el sistema se puede modelar como un conducto nico con una resistencia hidr ulica total que resulta de la suma de las resistencias individuales de cada secci n:

$\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$

(ID 11068)

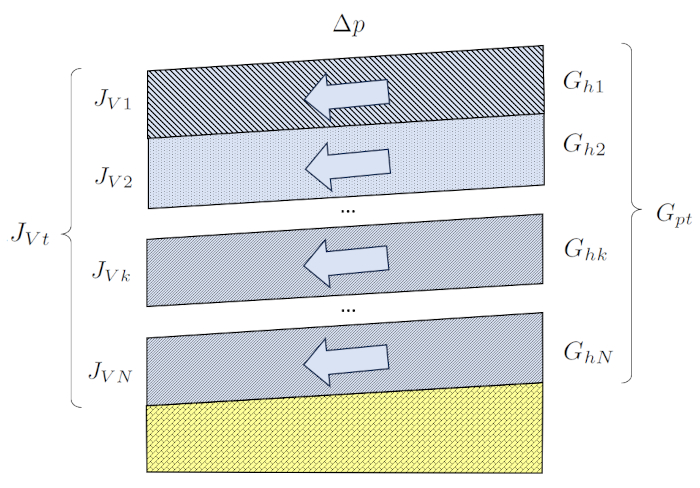
Una situaci n en el suelo en la que los elementos est n conectados en paralelo ocurre cuando el agua fluye a trav s de diferentes capas en paralelo. Si las capas tienen una inclinaci n, se genera una diferencia de presi n. Si las capas tienen un grosor similar, la diferencia de presi n ser igual en todas las capas. En este caso, el largo de la muestra ($\Delta L$) es constante, mientras que cada capa tiene una la sección de la k-esima capa ($S_k$) diferente.



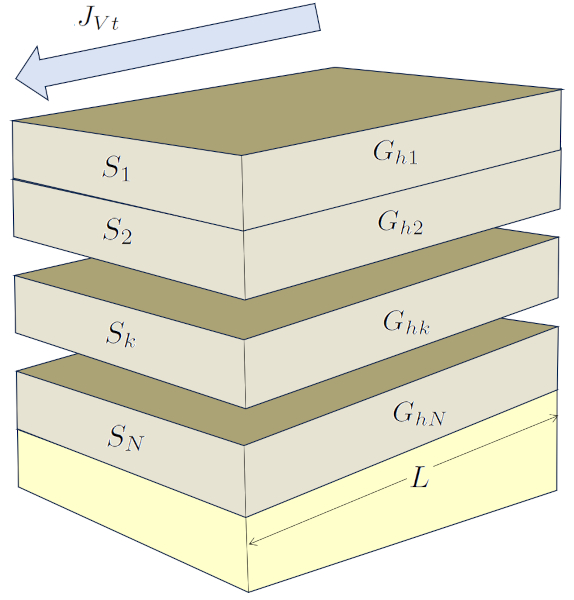
En esta situaci n, las conductividades hidr ulicas se suman directamente, y sus valores dependen del tipo de suelo, y, por lo tanto, de la conductividad hidráulica en la k-esima capa ($K_{sk}$) y la sección de la k-esima capa ($S_k$).

(ID 4373)


(ID 15223)

ID:(371, 0)