Usuario:
Diagrama de Fase
Storyboard 
La presión osmótica se genera en una solución cuando existe una membrana semipermeable. Esta membrana permite el paso del solvente, pero impide que el soluto la atraviese, lo que provoca un efecto de desequilibrio de presión. Como resultado, se produce una disminución de presión en el lado del solvente puro. Esta reducción impulsa el movimiento del solvente a través de la membrana hacia el lado que contiene el soluto. El proceso continúa hasta que la presión en el lado con soluto aumenta lo suficiente para equilibrar la disminución inicial de presión, o hasta que la dilución del soluto reduce el desequilibrio de presión, alcanzando un estado de equilibrio osmótico.
ID:(660, 0)
Diagrama de fase del agua
Concepto
Uno de los diagramas de fase más significativos para nuestro planeta es el del agua. Este diagrama presenta las tres fases clásicas: sólido, líquido y gas, además de una variedad de fases con diferentes estructuras cristalinas del hielo.
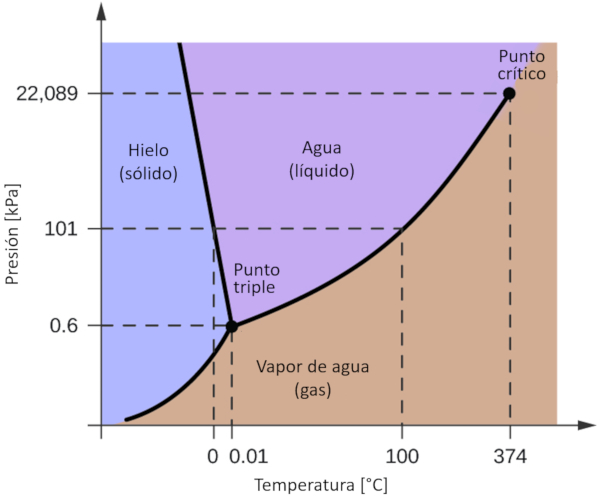
La característica más destacada en comparación con otros materiales es que en un rango de presión comprendido entre 611 Pa y 209.9 MPa, el estado sólido ocupa un volumen mayor que el estado líquido. Este fenómeno se refleja en el diagrama de fase como una pendiente negativa en la línea que separa las fases sólidas (hielo con estructura hexagonal) y líquidas (agua).
ID:(836, 0)
Fase gaseosa, vapor de agua
Concepto
La fase gaseosa, que en nuestro caso corresponde al vapor de agua, es aquella en la que los átomos pueden desplazarse relativamente libremente.
En esta fase, existe una interacción mínima que puede afectar el comportamiento de los átomos sin confinarlos de manera significativa.
ID:(15142, 0)
Fase liquida, agua
Concepto
La fase líquida, que en nuestro caso corresponde al agua, es aquella en la que los átomos pueden desplazarse relativa y libremente, manteniendo su unidad pero adaptándose a la forma que los contiene.
En esta fase, no se observa ninguna estructura definida.
ID:(15140, 0)
Fase solida, hielo
Concepto
La fase sólida, que en nuestro caso corresponde al hielo, es aquella en la que los átomos no pueden desplazarse relativamente y solo pueden oscilar en torno a su punto de equilibrio.
En esta fase, se puede observar una estructura que suele ser cristalina y, por lo tanto, regular.
ID:(15141, 0)
Presión osmótica
Modelo
La presión osmótica se genera en una solución cuando existe una membrana semipermeable. Esta membrana permite el paso del solvente, pero impide que el soluto la atraviese, lo que provoca un efecto de desequilibrio de presión. Como resultado, se produce una disminución de presión en el lado del solvente puro. Esta reducción impulsa el movimiento del solvente a través de la membrana hacia el lado que contiene el soluto. El proceso continúa hasta que la presión en el lado con soluto aumenta lo suficiente para equilibrar la disminución inicial de presión, o hasta que la dilución del soluto reduce el desequilibrio de presión, alcanzando un estado de equilibrio osmótico.
Variables
Cálculos
a 
,
luego, seleccione la variable: 
a 
Cálculos
Variable
Dado
Calcule
Objetivo :
Ecuación
A utilizar
Ecuaciones
(ID 4252)
Si hay la diferencia de presión ($\Delta p$) entre dos puntos, como lo indica la ecuaci n:
| $ dp = p - p_0 $ |
podemos usar la presión de la columna de agua ($p$), que es:
| $ p_t = p_0 + \rho_w g h $ |
Esto nos da:
$\Delta p=p_2-p_1=p_0+\rho_wh_2g-p_0-\rho_wh_1g=\rho_w(h_2-h_1)g$
Dado que la diferencia de altura ($\Delta h$) es:
| $ \Delta h = h_2 - h_1 $ |
la diferencia de presión ($\Delta p$) se puede expresar como:
| $ \Delta p = \rho_w g \Delta h $ |
(ID 4345)
El número de moles ($n$) corresponde a el número de partículas ($N$) dividido por el número de Avogadro ($N_A$):
| $ n \equiv\displaystyle\frac{ N_s }{ N_A }$ |
Si multiplicamos el numerador y el denominador por la masa de la partícula ($m$), obtenemos:
$n=\displaystyle\frac{N}{N_A}=\displaystyle\frac{Nm}{N_Am}=\displaystyle\frac{M}{M_m}$
As que es:
| $ n = \displaystyle\frac{ M }{ M_m }$ |
(ID 4854)
Como la energ a molar libre de Gibbs es
| $ dg = - s dT + v dp + \mu dN $ |
se tiene que para el equilibrio entre un sistema con y sin material disuelto (
$\displaystyle\frac{V}{N_A}dp=\displaystyle\frac{V}{N_A}(p - \Phi)=\mu dN=\mu (N-N_s)$
Como sin material disuelto se debe asumir que el vapor satisface la ecuaci n de los gases se tiene que
$\mu\sim \displaystyle\frac{R}{N_A} T$
con lo que se obtiene que
| $ \Psi =\displaystyle\frac{ N_s }{ V_C } R T $ |
(ID 12820)
(ID 12827)
Ejemplos
(ID 15287)
Cuando se coloca una membrana semipermeable en el fondo de un tubo en forma de U y se agrega agua, se puede observar que al agregar material disuelto, la columna con el soluto se eleva:
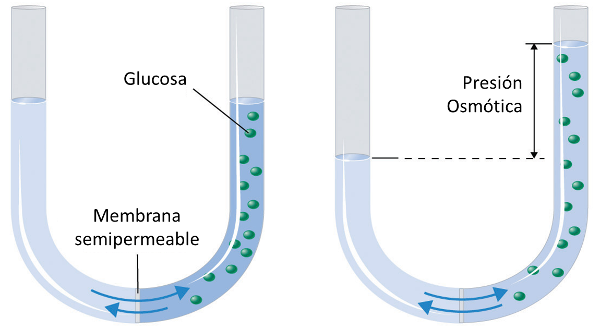
Esto se debe a la presi n negativa generada por la presi n osm tica.
(ID 2024)
(ID 15634)
ID:(660, 0)