Transferência de calor
Storyboard 
O calor é conduzido dentro de um meio até a interface com outro meio. Entre os dois, o calor é transferido com base na diferença de temperatura entre os meios, na superfície de contato e em uma constante de transferência térmica. Quando um dos meios é um gás (por exemplo, ar) ou um líquido (por exemplo, água), a constante de transferência térmica depende da estrutura da interface e da velocidade de fluxo do meio gasoso ou líquido.
ID:(776, 0)
Transporte de calor
Conceito 
O sistema básico inclui uma transferência gerada por la diferença de temperatura ($\Delta T$), que consiste de la diferença de temperatura na interface interna ($\Delta T_i$), la diferença de temperatura no condutor ($\Delta T_0$) e la diferença de temperatura na interface externa ($\Delta T_e$). Portanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Com la taxa de fluxo de calor ($q$) sendo responsável pela transferência entre o interior e o condutor, utilizando o coeficiente de transmissão interna ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
A condução envolve la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
E a transferência do condutor para o exterior, com o coeficiente de transmissão externa ($\alpha_e$), é representada por:
| $ q = \alpha_e \Delta T_e $ |
Tudo isso é representado graficamente por:
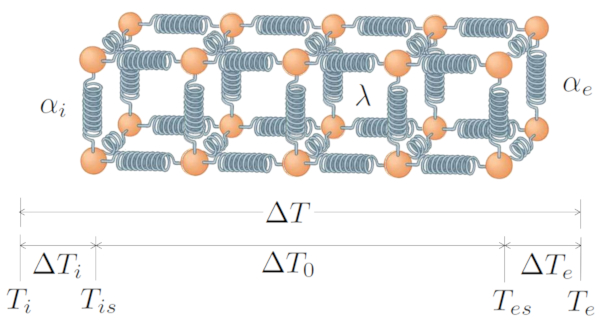
ID:(7723, 0)
Transferência de calor
Modelo 
O calor é conduzido dentro de um meio até a interface com outro meio. Entre os dois, o calor é transferido com base na diferença de temperatura entre os meios, na superfície de contato e em uma constante de transferência térmica. Quando um dos meios é um gás (por exemplo, ar) ou um líquido (por exemplo, água), a constante de transferência térmica depende da estrutura da interface e da velocidade de fluxo do meio gasoso ou líquido.
Variáveis
Cálculos
Cálculos
Equações
Exemplos
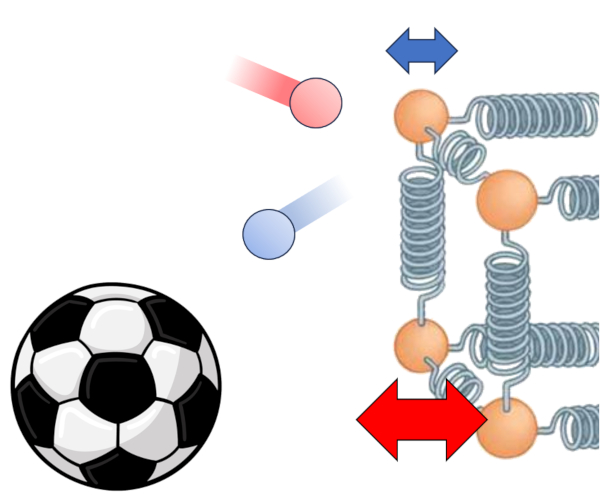
Considere um volume onde part culas colidem com as paredes a uma velocidade que representa a sua temperatura. Sempre que atingem uma grelha central, colidem com os tomos de um s lido, fazendo-os oscilar. Essa oscila o propaga-se atrav s do s lido at atingir a extremidade oposta, onde a energia transferida para o g s por meio de novas colis es.
Experimenta o:Pode-se ajustar a velocidade das part culas nas caixas laterais e observar como a energia transferida para o s lido e, a seguir, para o g s do lado oposto.
(ID 15276)
O principal impulsionador da transfer ncia de calor de um meio para um condutor a diferen a de temperatura. No meio la temperatura interna ($T_i$), as part culas t m mais energia e, ao colidirem com as do condutor a uma temperatura da superfície interna ($T_{is}$), tendem a aumentar a energia deste ltimo. Essa intera o pode ser representada da seguinte forma:
Al m da temperatura em si, o fluxo de calor depende de la diferença de temperatura na interface interna ($\Delta T_i$):
| $ \Delta T_i = T_i - T_{is} $ |
Outro fator fundamental o n mero de tomos aos quais a amplitude de oscila o pode ser aumentada, o que depende de la seção ($S$). Por fim, devemos considerar as propriedades da superf cie, descritas por o coeficiente de transmissão interna ($\alpha_i$), que corresponde rela o entre o calor transmitido, a rea superficial, a diferen a de temperatura e o tempo decorrido:
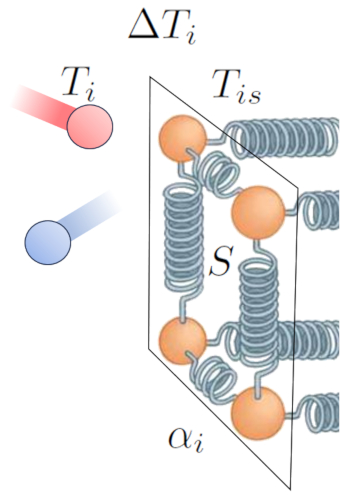
(ID 15237)
Dessa maneira, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) com base em la diferença de temperatura na interface interna ($\Delta T_i$) e o coeficiente de transmissão interna ($\alpha_i$):
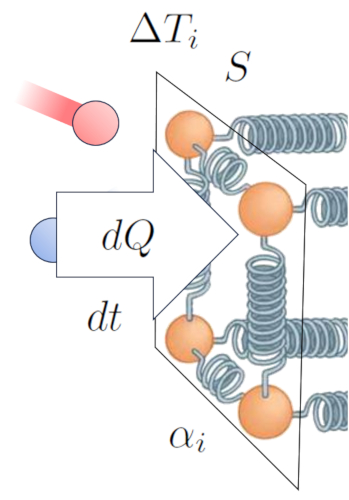
Isso pode ser expresso matematicamente da seguinte forma:
| $ q = \alpha_i \Delta T_i $ |
(ID 15238)
O principal impulsionador da transfer ncia de calor de um condutor para um meio a diferen a de temperatura. Quando la temperatura da superfície externa ($T_{es}$), as part culas t m mais energia e oscilam com uma amplitude maior ao interagirem com os tomos e mol culas do meio a uma temperatura externa ($T_e$). Isso tende a aumentar a energia destes ltimos. Essa intera o pode ser representada da seguinte forma:

Al m da temperatura, o fluxo de calor depende de la diferença de temperatura na interface externa ($\Delta T_e$).
| $ \Delta T_e = T_{es} - T_e $ |
Outro fator fundamental o n mero de tomos que podem ter aumentada a sua amplitude de oscila o, o que depende de la seção ($S$). Por fim, devemos considerar as propriedades superficiais, representadas por o coeficiente de transmissão externa ($\alpha_e$), que correspondem rela o entre o calor transmitido, a rea superficial, a diferen a de temperatura e o tempo decorrido:

(ID 15239)
Dessa forma, estabelecemos uma rela o que nos permite calcular la taxa de fluxo de calor ($q$) com base em la diferença de temperatura na interface externa ($\Delta T_e$) e o coeficiente de transmissão externa ($\alpha_e$):
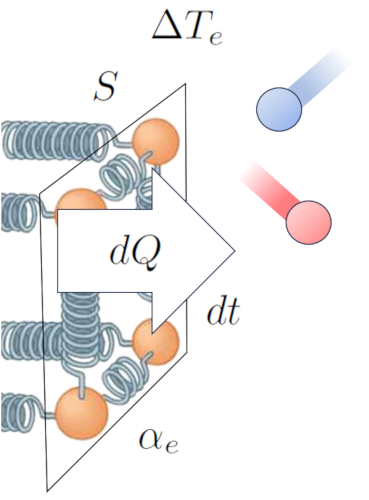
Isso pode ser expresso matematicamente da seguinte maneira:
| $ q = \alpha_e \Delta T_e $ |
(ID 15240)
A primeira descri o do modelo de transmiss o de calor na interface entre dois meios foi desenvolvida por Thomas Graham Balfour [1]. Sua teoria sugere que a taxa de calor transmitido depende da diferen a de temperatura e de uma constante espec fica da interface.
Quando o calor transferido para o condutor, representado por la taxa de fluxo de calor ($q$) juntamente com o coeficiente de transmissão interna ($\alpha_i$) e la diferença de temperatura na interface interna ($\Delta T_i$), a rela o expressa pela seguinte equa o:
| $ q = \alpha_i \Delta T_i $ |
No caso de o calor passar do condutor, identificado por la taxa de fluxo de calor ($q$) com o coeficiente de transmissão externa ($\alpha_e$) e la diferença de temperatura na interface externa ($\Delta T_e$), a rela o especificada como:
| $ q = \alpha_e \Delta T_e $ |
![]() [1] "The Theory of Heat" (A Teoria do Calor), Thomas Graham Balfour, 1876.
[1] "The Theory of Heat" (A Teoria do Calor), Thomas Graham Balfour, 1876.
(ID 15123)
O sistema b sico inclui uma transfer ncia gerada por la diferença de temperatura ($\Delta T$), que consiste de la diferença de temperatura na interface interna ($\Delta T_i$), la diferença de temperatura no condutor ($\Delta T_0$) e la diferença de temperatura na interface externa ($\Delta T_e$). Portanto:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Com la taxa de fluxo de calor ($q$) sendo respons vel pela transfer ncia entre o interior e o condutor, utilizando o coeficiente de transmissão interna ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
A condu o envolve la condutividade térmica ($\lambda$) e o comprimento do conductor ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
E a transfer ncia do condutor para o exterior, com o coeficiente de transmissão externa ($\alpha_e$), representada por:
| $ q = \alpha_e \Delta T_e $ |
Tudo isso representado graficamente por:
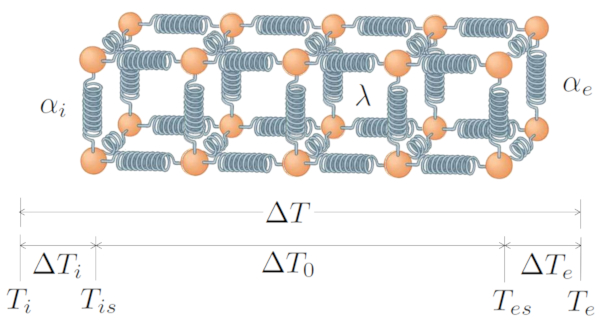
(ID 7723)
Um dos efeitos da transfer ncia de calor de um condutor para um meio externo o aquecimento do meio pr ximo interface, criando uma zona de interfer ncia na transmiss o. Isso diminui a efici ncia da transfer ncia e tende a formar uma camada isolante que reduz o fluxo de energia.
No entanto, esse efeito pode mudar na presen a de vento. O vento pode remover a camada de tomos e mol culas em alta temperatura, aumentando a efici ncia da transfer ncia de calor. Isso indica que o coeficiente de transmissão ($\alpha$) influenciado por la velocidade média ($v_m$) [1,2]:
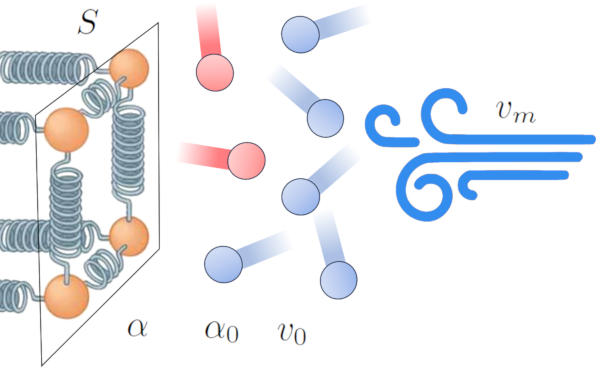
Nesse contexto, modelamos a rela o com base em ERROR:9844,0 e um fator de refer ncia de o velocidade de referência de mídia ($v_0$).
A rela o matem tica que descreve esse fen meno para um g s com o coeficiente de transmissão em gases, dependente da velocidade ($\alpha_{gv}$), la velocidade média ($v_m$), o coeficiente de transmissão em gases, independente da velocidade ($\alpha_{g0}$) e o coeficiente de transmissão fator de velocidade do gás ($v_{g0}$) :
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
E para um l quido com o coeficiente de transmissão em líquido, dependente da velocidade ($\alpha_{wv}$), la velocidade média ($v_m$), o coeficiente de transmissão em líquido, independente da velocidade ($\alpha_{w0}$) e o coeficiente de transmissão fator de velocidade do líquido ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Isso demonstra como o vento pode influenciar significativamente a efici ncia da transfer ncia de calor entre um condutor e um meio externo.![]() [1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sobre o Movimento de Fluidos com Muito Pouca Fric o), Ludwig Prandtl, 1904
[1] " ber Fl ssigkeitsbewegung bei sehr kleiner Reibung" (Sobre o Movimento de Fluidos com Muito Pouca Fric o), Ludwig Prandtl, 1904![]() [2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (A Depend ncia do Coeficiente de Transfer ncia de Calor com o Comprimento da Tubula o), Wilhelm Nusselt, 1910
[2] "Die Abh ngigkeit der W rme bergangszahl von der Rohrl nge" (A Depend ncia do Coeficiente de Transfer ncia de Calor com o Comprimento da Tubula o), Wilhelm Nusselt, 1910
(ID 3620)
(ID 15335)
ID:(776, 0)
