Interceptar a velocidad angular constante
Storyboard 
Los objetos pueden intersectarse cuando coinciden en ángulo en un mismo momento. Para lograrlo, deben desplazarse desde sus respectivos ángulos iniciales con velocidades angulares que les permitan coincidir en ángulo y tiempo al final del recorrido.
ID:(1450, 0)
Concepto de interceptar
Concepto 
En el caso de una intersección, se trata de dos cuerpos que se desplazan de tal manera que coincidirán en ERROR:10307,0 en el tiempo un tiempo de intersección ($t$).
Para lograr esto, cada cuerpo:
• Comienza su desplazamiento en el tiempo inicial del primer objeto ($t_1$) en el ángulo inicial del primer cuerpo ($\theta_1$) con una velocidad angular del cuerpo 1 ($\omega_1$).
• Comienza su desplazamiento en el tiempo inicial del segundo objeto ($t_2$) en el ángulo inicial del segundo cuerpo ($\theta_2$) con una velocidad angular del cuerpo 2 ($\omega_2$).
Estas condiciones deben cumplirse para lograr la intersección.
Con ello, los diagramas del ángulo en el tiempo pueden ser acoplados como se muestra en la siguiente representación:
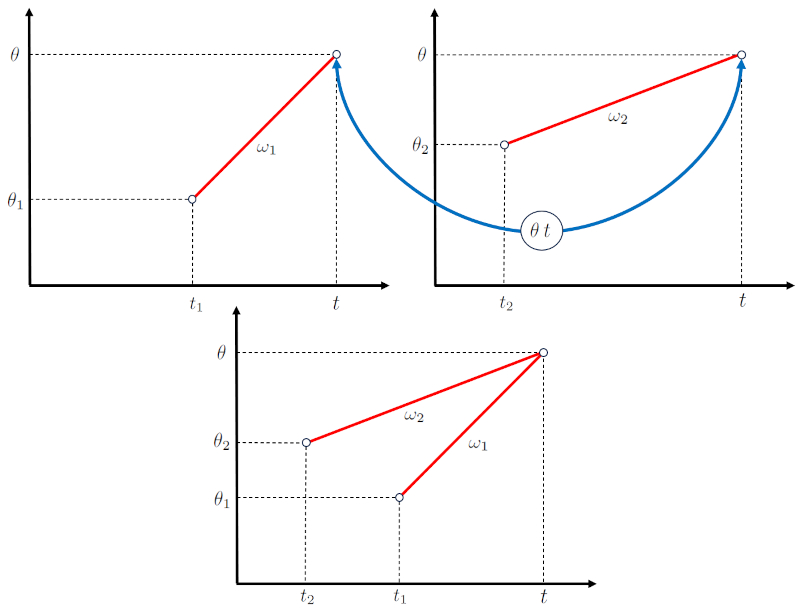
ID:(15517, 0)
Ángulos y duraciones de recorrido
Concepto 
En el caso de una intersección o choque entre dos objetos, es común que la velocidad angular del cuerpo 1 ($\omega_1$) y la velocidad angular del cuerpo 2 ($\omega_2$) deban estar configurados de manera que se produzca la coincidencia.
Esto implica que el ángulo recorrido por el primer cuerpo ($\Delta\theta_1$) y la duración del viaje del primer objeto ($\Delta t_1$) deben resultar en una velocidad angular del cuerpo 1 ($\omega_1$),
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
de manera que, con el ángulo recorrido por el segundo cuerpo ($\Delta\theta_2$) y la duración de viaje del segundo objeto ($\Delta t_2$), se obtenga una velocidad angular del cuerpo 2 ($\omega_2$),
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
para que finalmente coincidan en tiempo y espacio (posición):
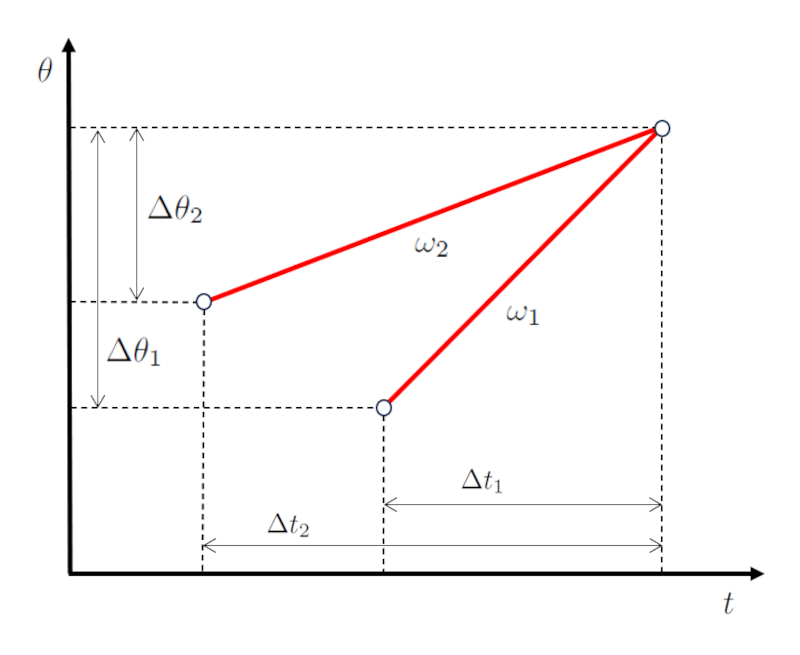
ID:(15516, 0)
Ángulo y tiempo al interceptar
Concepto 
En el caso de un movimiento en el que dos objetos se interceptan, como la ángulo de la intersección ($\theta$) y el tiempo de intersección ($t$), es común para ambos. Por lo tanto, si para el primer objeto, el tiempo inicial del primer objeto ($t_1$) y el ángulo inicial del primer cuerpo ($\theta_1$) con la velocidad angular del cuerpo 1 ($\omega_1$) cumplen:
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
y para el segundo objeto, el tiempo inicial del segundo objeto ($t_2$) y el ángulo inicial del segundo cuerpo ($\theta_2$) con la velocidad angular del cuerpo 2 ($\omega_2$) se cumplen:
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
Esto se representa como:

ID:(15518, 0)
Interceptar a velocidad angular constante
Modelo 
Los objetos pueden intersectarse cuando coinciden en ángulo en un mismo momento. Para lograrlo, deben desplazarse desde sus respectivos ángulos iniciales con velocidades angulares que les permitan coincidir en ángulo y tiempo al final del recorrido.
Variables
Cálculos
Cálculos
Ecuaciones
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
En el caso de que la velocidad angular inicial ($\omega_0$) sea igual a la velocidad angular media ($\bar{\omega}$),
| $ \bar{\omega} = \omega_0 $ |
Por lo tanto, con la diferencia de ángulos ($\Delta\theta$), que es igual a el ángulo ($\theta$) dividido por el ángulo inicial ($\theta_0$), obtenemos:
| $ \Delta\theta = \theta_2 - \theta_1 $ |
Y con el tiempo transcurrido ($\Delta t$), que es igual a el tiempo ($t$) dividido por el tiempo inicial ($t_0$), obtenemos:
| $ \Delta t \equiv t - t_0 $ |
Podemos reescribir la ecuaci n de la velocidad angular media ($\bar{\omega}$) como:
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
Esto se puede expresar como:
$\omega_0 = \omega = \displaystyle\frac{\Delta\theta}{\Delta t} = \displaystyle\frac{\theta - \theta_0}{t - t_0}$
Despejando, obtenemos:
| $ \theta = \theta_0 + \omega_0 ( t - t_0 )$ |
(ID 1023)
Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son
| $ \Delta s=r \Delta\theta $ |
y la definici n de la velocidad angular media ($\bar{\omega}$) es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en
| $ v = r \omega $ |
.
(ID 3233)
Como la velocidad media ($\bar{v}$) es con la distancia recorrida en un tiempo ($\Delta s$) y el tiempo transcurrido ($\Delta t$), igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y con la distancia recorrida en un tiempo ($\Delta s$) expresado como arco de un c rculo, y el radio ($r$) y la variación del angulo ($\Delta\theta$) son
| $ \Delta s=r \Delta\theta $ |
y la definici n de la velocidad angular media ($\bar{\omega}$) es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relaci n es general, se puede aplicar para valores instant neos, lo que resulta en
| $ v = r \omega $ |
.
(ID 3233)
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
y el tiempo transcurrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
La definici n de la velocidad angular media ($\bar{\omega}$) se considera la variación del angulo ($\Delta\theta$),
| $ \Delta\theta = \theta_2 - \theta_1 $ |
y el tiempo transcurrido ($\Delta t$),
| $ \Delta t \equiv t - t_0 $ |
La relaci n entre ambos se define como la velocidad angular media ($\bar{\omega}$):
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
(ID 3679)
Ejemplos
(ID 15411)
En el caso de una intersecci n, se trata de dos cuerpos que se desplazan de tal manera que coincidir n en ERROR:10307,0 en el tiempo un tiempo de intersección ($t$).
Para lograr esto, cada cuerpo:
• Comienza su desplazamiento en el tiempo inicial del primer objeto ($t_1$) en el ángulo inicial del primer cuerpo ($\theta_1$) con una velocidad angular del cuerpo 1 ($\omega_1$).
• Comienza su desplazamiento en el tiempo inicial del segundo objeto ($t_2$) en el ángulo inicial del segundo cuerpo ($\theta_2$) con una velocidad angular del cuerpo 2 ($\omega_2$).
Estas condiciones deben cumplirse para lograr la intersecci n.
Con ello, los diagramas del ngulo en el tiempo pueden ser acoplados como se muestra en la siguiente representaci n:

(ID 15517)
En el caso de una intersecci n o choque entre dos objetos, es com n que la velocidad angular del cuerpo 1 ($\omega_1$) y la velocidad angular del cuerpo 2 ($\omega_2$) deban estar configurados de manera que se produzca la coincidencia.
Esto implica que el ángulo recorrido por el primer cuerpo ($\Delta\theta_1$) y la duración del viaje del primer objeto ($\Delta t_1$) deben resultar en una velocidad angular del cuerpo 1 ($\omega_1$),
| $ \omega_1 \equiv\displaystyle\frac{ \Delta\theta_1 }{ \Delta t_1 }$ |
de manera que, con el ángulo recorrido por el segundo cuerpo ($\Delta\theta_2$) y la duración de viaje del segundo objeto ($\Delta t_2$), se obtenga una velocidad angular del cuerpo 2 ($\omega_2$),
| $ \omega_2 \equiv\displaystyle\frac{ \Delta\theta_2 }{ \Delta t_2 }$ |
para que finalmente coincidan en tiempo y espacio (posici n):

(ID 15516)
En el caso de un movimiento en el que dos objetos se interceptan, como la ángulo de la intersección ($\theta$) y el tiempo de intersección ($t$), es com n para ambos. Por lo tanto, si para el primer objeto, el tiempo inicial del primer objeto ($t_1$) y el ángulo inicial del primer cuerpo ($\theta_1$) con la velocidad angular del cuerpo 1 ($\omega_1$) cumplen:
| $ \theta = \theta_1 + \omega_1 ( t - t_1 )$ |
y para el segundo objeto, el tiempo inicial del segundo objeto ($t_2$) y el ángulo inicial del segundo cuerpo ($\theta_2$) con la velocidad angular del cuerpo 2 ($\omega_2$) se cumplen:
| $ \theta = \theta_2 + \omega_2 ( t - t_2 )$ |
Esto se representa como:

(ID 15518)
(ID 15422)
ID:(1450, 0)
