Tiefe Zirkulationsströme
Storyboard 
Es gibt mehrere Punkte, an denen Strömungen von der ozeanischen Oberfläche in größere Tiefen führen und so eine tiefgehende Zirkulation erzeugen. Diese Zirkulation unterliegt der Corioliskraft, was zu Abweichungen und einigen Strömungen zur Oberfläche (Auftrieb) führt, die mit Oberflächenströmungen verbunden sind.Das klassische Modell für diese Strömungen ist das von Stommel und Arons, das, obwohl einfach, die beobachteten unterschiedlichen Tiefenströmungen erklärt.[1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
ID:(1623, 0)
Thermohaline Zirkulation
Konzept 
Die tiefere Zirkulation wird als thermohaline Zirkulation (THC) bezeichnet, da ihre Bewegung mit Variationen der Temperatur (thermo) und Salinität (halin) verbunden ist. Um zu verstehen, wie dies geschieht, müssen wir zunächst die Struktur des Systems beschreiben.
In vereinfachter Form kann der Ozean als ein System mit drei Schichten modelliert werden:
- Eine obere Schicht, in der die Wasserbewegung durch luftgetriebene Strömungen erzeugt wird.
- Eine mittlere Schicht, deren Bewegung durch Dichteunterschiede im Ozean verursacht wird, die auf Unterschiede in Temperatur und Salinität zurückzuführen sind (thermohalin).
- Eine tiefe Schicht, die als ruhend angenommen werden kann.
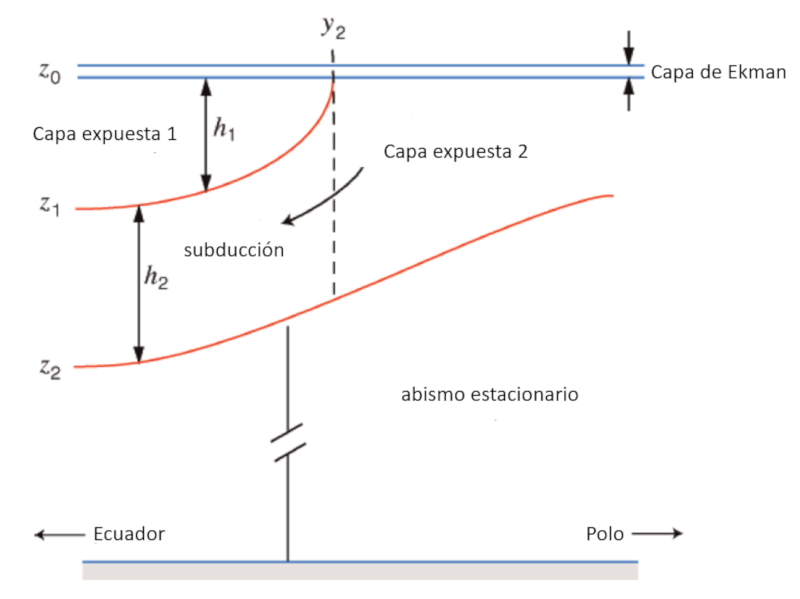
Der Anstieg der Dichte in Richtung der Pole, wo das Wasser kälter ist, führt dazu, dass das Wasser buchstäblich absinkt und eine Subduktion unterhalb der oberen Schicht erzeugt. Das folgende Diagramm fasst den beschriebenen Prozess zusammen:
ID:(12095, 0)
Thermohaline Zirkulation über dem Planeten
Beschreibung 
Wenn wir den Globus betrachten, entsteht die thermohaline Zirkulation in der Nähe eines der Pole (Nord oder Süd) durch Wasser, das aufgrund einer höheren Salinität und niedrigeren Temperaturen zu sinken beginnt. Der Fluss dieser Zirkulation geht in Richtung des Äquators und erzeugt eine Aufwärtsbewegung, bei der Wasser teilweise aufsteigt und in Richtung des Pols fließt, um das absteigende Wasser zu ersetzen.
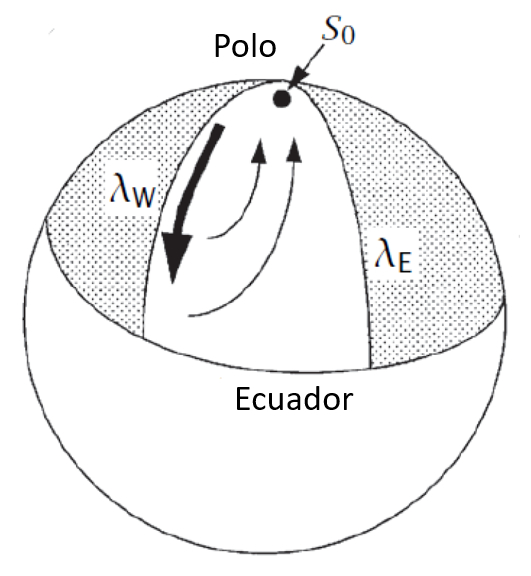
Darstellung des Nordatlantiks im Stommel- und Arons-Modell [1], [2]
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Über die abyssale Zirkulation des Weltmeeres - I. Stationäre planetare Strömungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Über die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12096, 0)
Boxmodell
Beschreibung 
Das Modell von Stommel und Arons [1], [2] betrachtet den Ozean als eine zweidimensionale Box mit Koordinaten auf den Achsen x und y. Speziell:
- Koordinaten auf der x-Achse: $x_w$ (Westen) und $x_e$ (Osten).
- Koordinaten auf der y-Achse: $y_s$ (Süden) und $y_n$ (Norden).
Diese Koordinaten sind in folgender Grafik dargestellt:
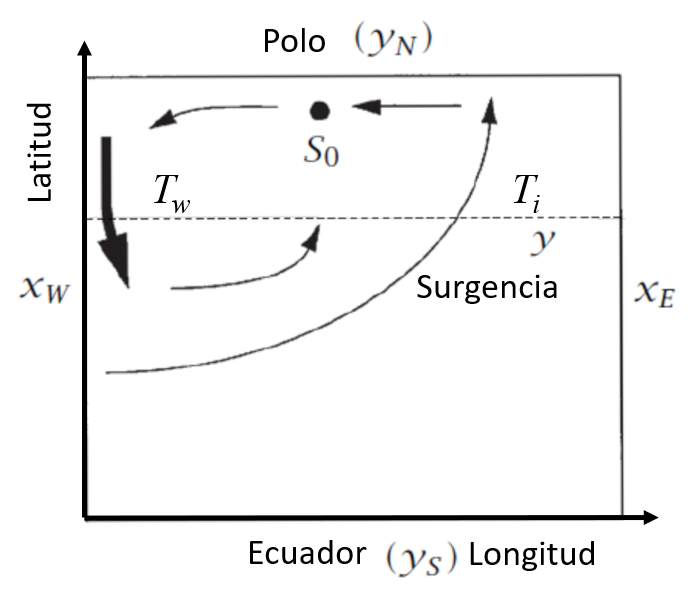
Atlantic-Box-Modell [1], [2].
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Über die abyssale Zirkulation des Weltmeeres - I. Stationäre planetare Strömungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Über die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12082, 0)
Charakteristische Zeiten
Beschreibung 
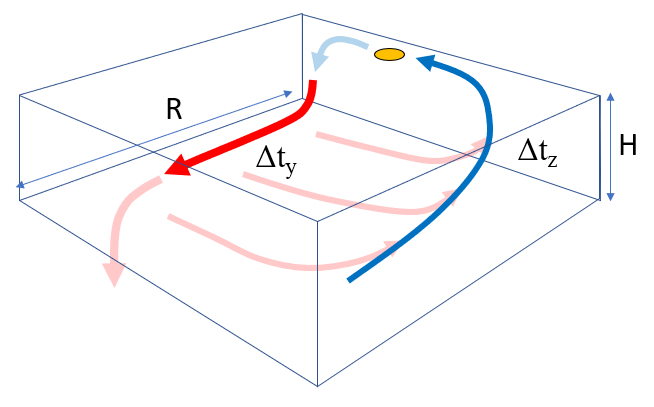
Jeder Schritt ist mit einer charakteristischen Zeit verbunden:
- Reisezeit mit dem Haupt-Fluss $\Delta t_y$
- Ablenkungszeit mit dem Verlust-Fluss $\Delta t_x$
- Auftriebszeit $\Delta t_z$
ID:(13426, 0)
Geschwindigkeiten und Beschleunigungen pro Fluss
Beschreibung 
Jede charakteristische Zeit wird mit Geschwindigkeiten und Beschleunigungen entlang des zurückgelegten Weges assoziiert:
- Mit dem Hauptfluss $v_y, a_y$.
- Mit dem Verlustfluss $v_x, a_x$.
- Mit der Aufwärtsbewegung $v_z, a_z$.
Im Allgemeinen löst die Anfangsgeschwindigkeit (
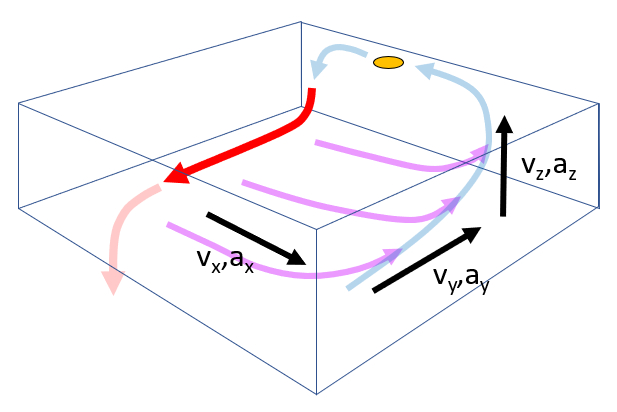
ID:(13427, 0)
Verlorene Strömungsgeometrie
Beschreibung 
Der Verlustfluss ist nicht gleichmäßig und verteilt sich entlang der Breitengrade, daher wird er entsprechend seines Abstands zur nördlichsten Position modelliert. Somit ist er in nördlichen Breitengraden null und maximal am südlichen Rand des Rechtecks, in dem die Zirkulation modelliert wird:
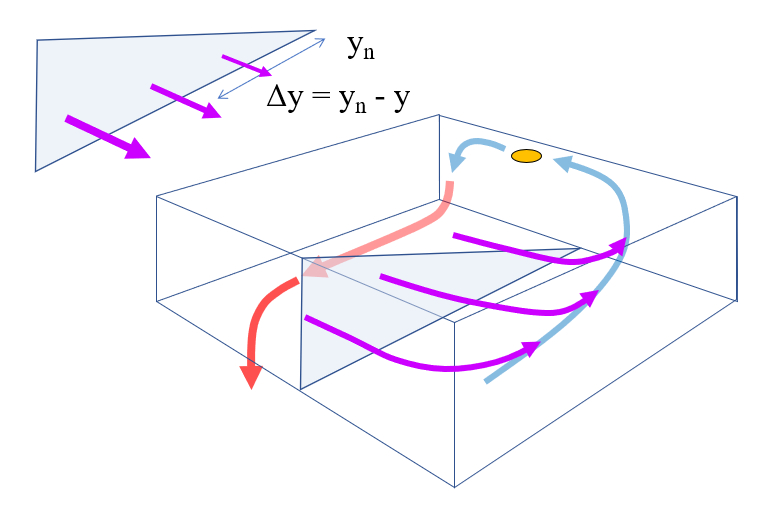
ID:(13428, 0)
Auftriebsströmungsgeometrie
Beschreibung 
Da der Verlustfluss nicht gleichmäßig ist, ist auch die Auftriebsströmung nicht gleichmäßig. Innerhalb des gleichen Modells wird angenommen, dass die Auftriebsströmung am östlichen Rand des Rechtecks, in dem die Zirkulation modelliert wird, maximal ist. Ähnlich wie beim Verlust wird eine lineare Beziehung angenommen:
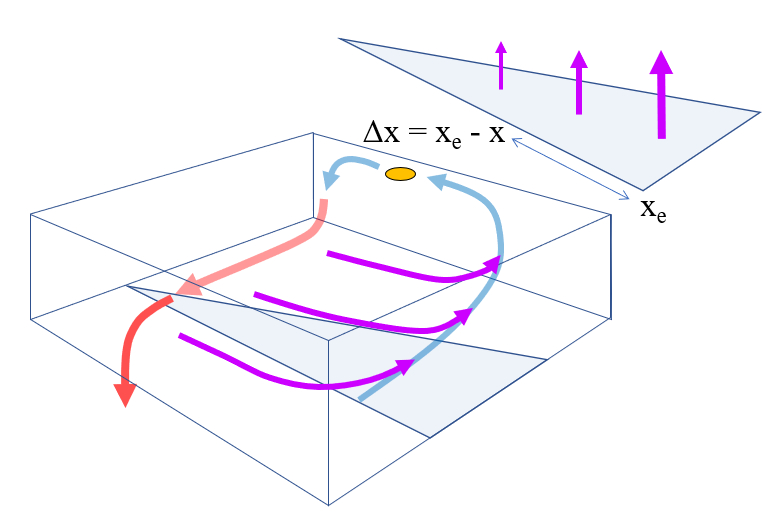
ID:(13429, 0)
Hauptflüsse tiefer Strömungen
Beschreibung 
In der Modellierung des Tiefenflusses sind vier Strömungen zu berücksichtigen:
Der Hauptfluss $F_w$, der sich entlang des Meeresbodens bewegt.
Der Verlustfluss $F_i$, der aufgrund der Corioliskraft abgelenkt wird.
Der Auftriebsfluss $U_x$, der dem Anteil des Verlustflusses entspricht, der die Oberfläche erreicht.
Der Sinkfluss $S_0$, der aus den Oberflächenströmungen stammt und auch die zurückgesunkenen Verluste einschließt.
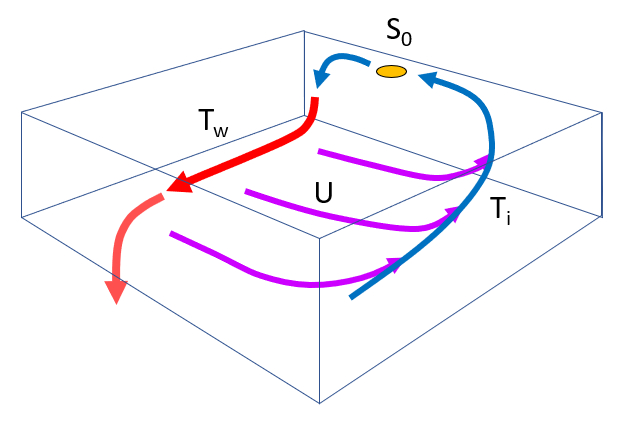
ID:(13425, 0)
Unterwasserströmungen und Coriolis
Beschreibung 
Die sogenannte Coriolis-Kraft spielt eine wesentliche Rolle in der Dynamik des Wassers an den Polen und beeinflusst, wie Wassermassen aufgrund von Temperatur- und Salinitätsunterschieden absteigen.
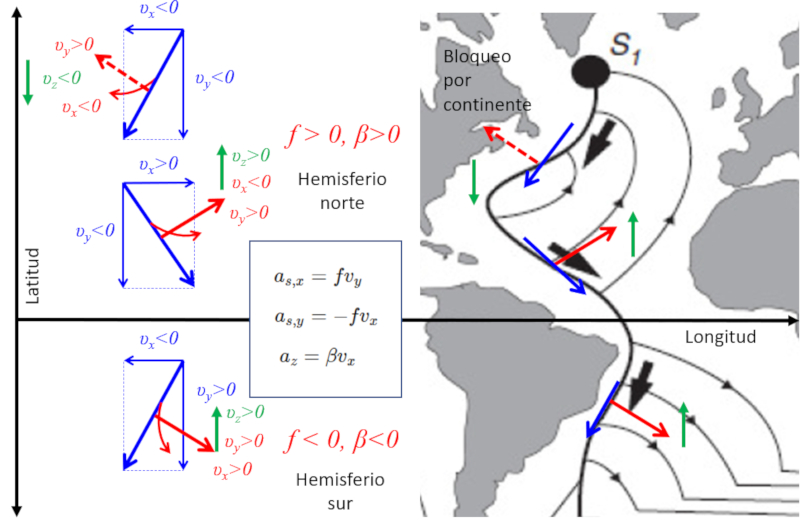
Bei der Analyse des Atlantischen Ozeans kann man eine Bewegung des Wassers vom Pol zum Äquator beobachten, die nach Westen abgelenkt wird. Dieses Phänomen wird durch die Verzögerung im Vergleich zur Rotation des Planeten verursacht, wenn man von einer Zone geringerer Geschwindigkeit entlang der Breitengrade zu einer Zone höherer Geschwindigkeit übergeht. Dieses Verhalten kann mit der Coriolis-Gleichung für die x-Richtung modelliert werden, die durch coriolis-Beschleunigung an der Oberfläche in x-Richtung $m/s^2$, coriolis-Faktor $rad/s$ und geschwindigkeit im Meridian $m/s$ gegeben ist:
| $ a_{c,x} = f v_y $ |
In dieser Gleichung ist der Coriolis-Faktor
Die geografische Kontur des Kontinents ermöglicht eine Bewegung in der x-Richtung (Längengrad), was zu einer Beschleunigung in der y-Richtung (Breitengrad) führt. Diese kann mit coriolis-Beschleunigung an der Oberfläche in y-Richtung $m/s^2$, coriolis-Faktor $rad/s$ und parallelgeschwindigkeit $m/s$ berechnet werden:
| $ a_{c,y} = - f v_x $ |
Diese Berechnung zeigt, dass in der Nähe des Äquators Verschiebungen auftreten, bei denen Wasser von der Hauptströmung weg und nach Norden bewegt wird. Wenn wir die Beschleunigung in der z-Richtung (Tiefe) betrachten und berücksichtigen, dass
| $ a_{cz} = R \beta v_x $ |
.
ID:(12122, 0)
Stommel-Arons-Tiefenströmungen
Beschreibung 
Am Ende lösen Stommel und Arons [1], [2] das Modell und zeigen die wichtigsten Tiefenströmungen, die weltweit existieren:
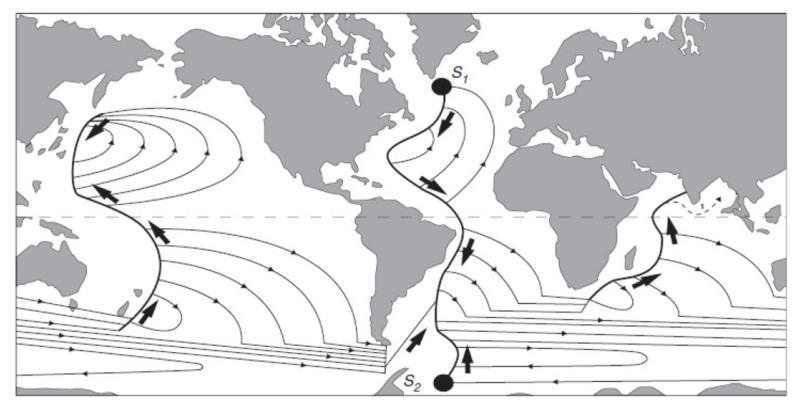
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Über die abyssale Zirkulation des Weltmeeres - I. Stationäre planetare Strömungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Über die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12099, 0)
Struktur des Stommel-Arons-Modells
Beschreibung 
Als Stommel und Arons [1], [2] ihr erstes Modell der thermohalinen Zirkulation entwickelten, unterteilten sie die verschiedenen Ozeane in Zonen mit definierter Auftriebsströmung (nach oben zeigende Pfeile) und zwei Quellen, eine in der Arktis und eine andere in der Antarktis:
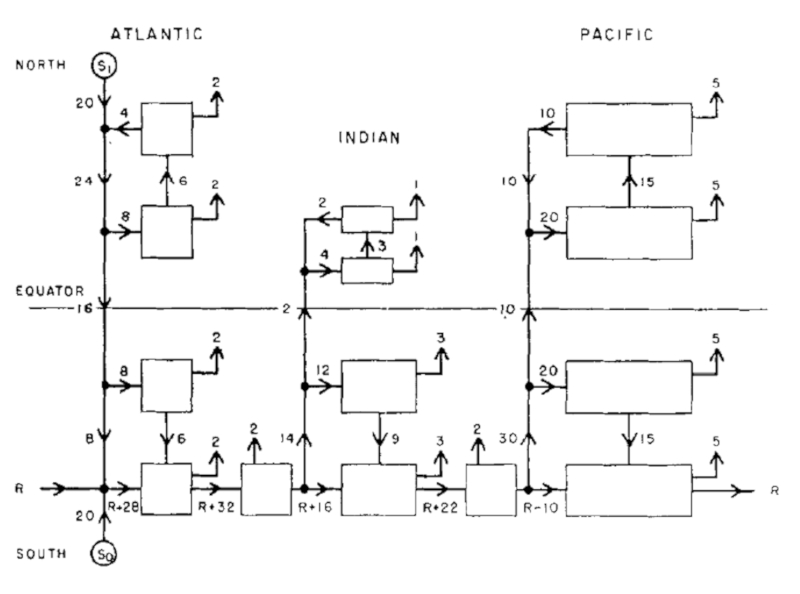
Globales Zirkulationsmodell in Sv (Sverdrup) ($10^6 m^3/s$) [2].
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. (Über die abyssale Zirkulation des Weltmeeres - I. Stationäre planetare Strömungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. (Über die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
ID:(12098, 0)
Echte thermohaline Zirkulation
Beschreibung 
Messungen haben gezeigt, dass die thermohaline Zirkulation ein integriertes System ist, das den gesamten Globus umspannt. Es gibt mindestens zwei Punkte, die als Quellen betrachtet werden können, und ihr Verlauf erstreckt sich über alle Ozeane.
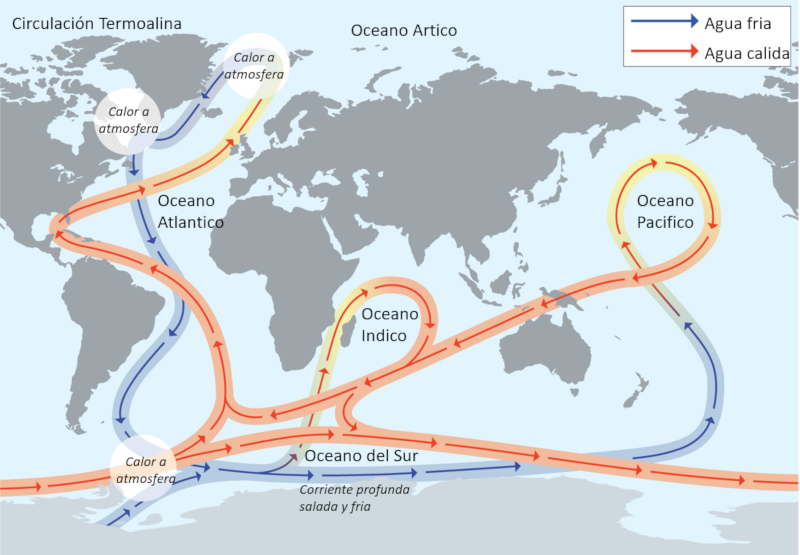
ID:(12097, 0)
Untersuchung des möglichen Zusammenbruchs der Tiefenströmung
Beschreibung 
Durch mehrere Simulationen werden die Auswirkungen der polaren Eisschmelze auf das Absinken und dessen Einfluss auf die Tiefenzirkulation untersucht. Es gibt Anzeichen dafür, dass die Zirkulation bereits rückläufig ist. Ein Zusammenbruch der Tiefenzirkulation bedeutet jedoch nicht zwangsläufig dasselbe für die Oberflächenzirkulation, die durch Winde angetrieben wird. Was passieren könnte, ist eine Verschiebung in der Oberflächenzirkulation, was zu einer Verringerung des Beitrags des Golfstroms an warmem Wasser für Nordeuropa führt.
Das folgende Diagramm zeigt Variationen im Fluss in Einheiten von Sv (Sverdrup), was etwa $10^6,m^3/s$ entspricht:
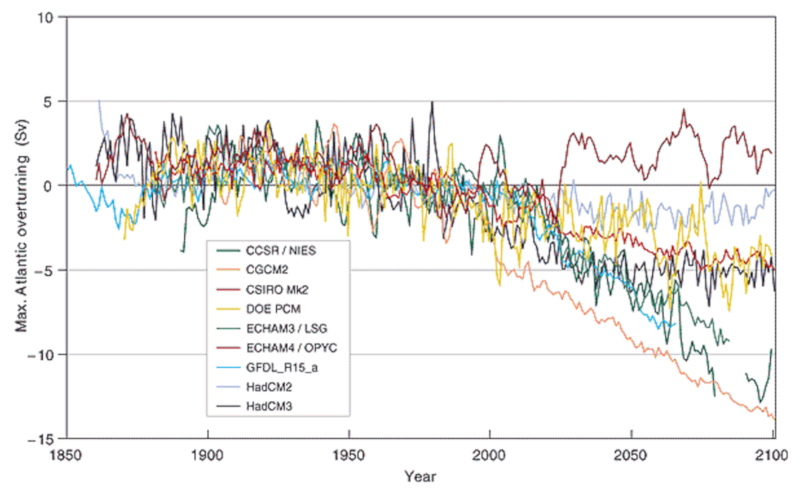
Unter der Annahme einer Absinkrate von etwa 20 Sv lässt sich schlussfolgern, dass in einigen Simulationen die Tiefenzirkulation zum Stillstand kommt. Diese Variationen sind mit verschiedenen zukünftigen Szenarien menschlicher Aktivitäten und Überlegungen zu Aspekten verbunden, bei denen es weniger Gewissheit über ihr Eintreten gibt. Detailliertere Informationen finden sich in den Berichten des Intergovernmental Panel on Climate Change (IPCC).
ID:(13430, 0)
Tiefe Zirkulationsströme
Modell 
Es gibt mehrere Punkte, an denen Strömungen von der ozeanischen Oberfläche in größere Tiefen führen und so eine tiefgehende Zirkulation erzeugen. Diese Zirkulation unterliegt der Corioliskraft, was zu Abweichungen und einigen Strömungen zur Oberfläche (Auftrieb) führt, die mit Oberflächenströmungen verbunden sind. Das klassische Modell für diese Strömungen ist das von Stommel und Arons, das, obwohl einfach, die beobachteten unterschiedlichen Tiefenströmungen erklärt. [1] Ocean Circulation Theory, Joseph Pedlosky, Springer 1998 (7.3 Stommel-Arons Theory: Abyssal Flow on the Sphere)
Variablen
Berechnungen
Berechnungen
Gleichungen
Da die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) aus die Winkelgeschwindigkeit des Planeten ($\omega$), die Breitengrad ($\varphi$), die Geschwindigkeit y des Objekt ($v_y$) und die Geschwindigkeit z des Objekt ($v_z$) besteht:
| $ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$ |
und die Definition von der Coriolis-Faktor ($f$) lautet:
| $ f = 2 \omega \sin \varphi $ |
zus tzlich zur Einschr nkung der Bewegung auf der Oberfl che, wo:
$v_z = 0$
ergibt sich, dass die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$) ist:
| $ a_{c,x} = f v_y $ |
(ID 11698)
Da die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$) aus die Winkelgeschwindigkeit des Planeten ($\omega$), die Geschwindigkeit x des Objekt ($v_x$) und die Breitengrad ($\varphi$) besteht:
| $ a_{c,y} = -2 \omega v_x \sin \varphi$ |
und die Definition von der Coriolis-Faktor ($f$) lautet:
| $ f = 2 \omega \sin \varphi $ |
zus tzlich zur Einschr nkung der Bewegung auf der Oberfl che, wo gilt:
$v_z = 0$
f hrt dies dazu, dass die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$) folgenderma en ist:
| $ a_{c,y} = - f v_x $ |
(ID 11699)
(ID 12083)
(ID 12084)
Wenn wir typische Zeitskalen f r jede Dimension einf hren, k nnen wir die Coriolis-Beschleunigungen als Geschwindigkeiten geteilt durch ihre typischen Zeitskalen absch tzen, n mlich:
$v_i =a_i \Delta t_i$
mit
| $ a_{cz} = R \beta v_x $ |
Somit erhalten wir:
$v_z=\beta R v_x\Delta t_z$
Auf der anderen Seite haben wir mit der Gleichung f r die
$v_x=\displaystyle\frac{v_y}{f\Delta t_y}$
Durch Ersetzen von
| $ v_z =\displaystyle\frac{ \beta }{ f }\displaystyle\frac{ \Delta t_z }{ \Delta t_y } R v_y $ |
(ID 12089)
(ID 12093)
Bei einer Bewegung in Richtung x (Ost-West) entsteht die Coriolis-Beschleunigung in z-Richtung ($a_{c,z}$) mit die Geschwindigkeit x des Objekt ($v_x$), die Winkelgeschwindigkeit des Planeten ($\omega$) und die Breitengrad ($\varphi$):
| $ a_{c,z} = 2 \omega v_x \cos \varphi$ |
Dies wird erg nzt durch die Coriolis-Beschleunigung an der Oberfläche in x-Richtung ($a_{c,x}$) (Ost-West) mit der Coriolis-Faktor ($f$) und die Geschwindigkeit y des Objekt ($v_y$):
| $ a_{c,x} = f v_y $ |
und die Coriolis-Beschleunigung an der Oberfläche in y-Richtung ($a_{c,y}$) (Nord-S d) mit der Coriolis-Faktor ($f$) und die Geschwindigkeit x des Objekt ($v_x$), das definiert ist als:
| $ a_{c,y} = - f v_x $ |
Wo der Coriolis-Faktor ($f$) definiert ist als:
| $ f = 2 \omega \sin \varphi $ |
Deshalb k nnen wir der Coriolis-Beta-Faktor ($\beta$) einf hren, definiert als:
| $ \beta =\displaystyle\frac{ 2 \omega \cos \varphi }{ R }$ |
Dadurch erhalten wir:
| $ a_{cz} = R \beta v_x $ |
(ID 12104)
In Analogie zu der Coriolis-Faktor ($f$), definiert mit die Breitengrad ($\varphi$) und die Winkelgeschwindigkeit des Planeten ($\omega$) als:
| $ f = 2 \omega \sin \varphi $ |
variiert der Faktor im Bogen $R\theta$, mit der Planetenradio ($R$) und die Breitengrad ($\varphi$) als Breitengrad, gem :
$\displaystyle\frac{\partial f}{\partial (R\varphi) }=\displaystyle\frac{ 2\omega\cos\varphi }{R}$
deshalb kann der Coriolis-Beta-Faktor ($\beta$) definiert werden als:
| $ \beta =\displaystyle\frac{ 2 \omega \cos \varphi }{ R }$ |
(ID 12105)
(ID 16211)
Beispiele
(ID 15584)
Die tiefere Zirkulation wird als thermohaline Zirkulation (THC) bezeichnet, da ihre Bewegung mit Variationen der Temperatur (thermo) und Salinit t (halin) verbunden ist. Um zu verstehen, wie dies geschieht, m ssen wir zun chst die Struktur des Systems beschreiben.
In vereinfachter Form kann der Ozean als ein System mit drei Schichten modelliert werden:
- Eine obere Schicht, in der die Wasserbewegung durch luftgetriebene Str mungen erzeugt wird.
- Eine mittlere Schicht, deren Bewegung durch Dichteunterschiede im Ozean verursacht wird, die auf Unterschiede in Temperatur und Salinit t zur ckzuf hren sind (thermohalin).
- Eine tiefe Schicht, die als ruhend angenommen werden kann.
Der Anstieg der Dichte in Richtung der Pole, wo das Wasser k lter ist, f hrt dazu, dass das Wasser buchst blich absinkt und eine Subduktion unterhalb der oberen Schicht erzeugt. Das folgende Diagramm fasst den beschriebenen Prozess zusammen:

(ID 12095)
Wenn wir den Globus betrachten, entsteht die thermohaline Zirkulation in der N he eines der Pole (Nord oder S d) durch Wasser, das aufgrund einer h heren Salinit t und niedrigeren Temperaturen zu sinken beginnt. Der Fluss dieser Zirkulation geht in Richtung des quators und erzeugt eine Aufw rtsbewegung, bei der Wasser teilweise aufsteigt und in Richtung des Pols flie t, um das absteigende Wasser zu ersetzen.

Darstellung des Nordatlantiks im Stommel- und Arons-Modell [1], [2]
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. ( ber die abyssale Zirkulation des Weltmeeres - I. Station re planetare Str mungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. ( ber die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
(ID 12096)
Das Modell von Stommel und Arons [1], [2] betrachtet den Ozean als eine zweidimensionale Box mit Koordinaten auf den Achsen x und y. Speziell:
- Koordinaten auf der x-Achse: $x_w$ (Westen) und $x_e$ (Osten).
- Koordinaten auf der y-Achse: $y_s$ (S den) und $y_n$ (Norden).
Diese Koordinaten sind in folgender Grafik dargestellt:

Atlantic-Box-Modell [1], [2].
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. ( ber die abyssale Zirkulation des Weltmeeres - I. Station re planetare Str mungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. ( ber die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
(ID 12082)
Jeder Schritt ist mit einer charakteristischen Zeit verbunden:
- Reisezeit mit dem Haupt-Fluss $\Delta t_y$
- Ablenkungszeit mit dem Verlust-Fluss $\Delta t_x$
- Auftriebszeit $\Delta t_z$

(ID 13426)
Jede charakteristische Zeit wird mit Geschwindigkeiten und Beschleunigungen entlang des zur ckgelegten Weges assoziiert:
- Mit dem Hauptfluss $v_y, a_y$.
- Mit dem Verlustfluss $v_x, a_x$.
- Mit der Aufw rtsbewegung $v_z, a_z$.
Im Allgemeinen l st die Anfangsgeschwindigkeit (

(ID 13427)
Der Verlustfluss ist nicht gleichm ig und verteilt sich entlang der Breitengrade, daher wird er entsprechend seines Abstands zur n rdlichsten Position modelliert. Somit ist er in n rdlichen Breitengraden null und maximal am s dlichen Rand des Rechtecks, in dem die Zirkulation modelliert wird:

(ID 13428)
Da der Verlustfluss nicht gleichm ig ist, ist auch die Auftriebsstr mung nicht gleichm ig. Innerhalb des gleichen Modells wird angenommen, dass die Auftriebsstr mung am stlichen Rand des Rechtecks, in dem die Zirkulation modelliert wird, maximal ist. hnlich wie beim Verlust wird eine lineare Beziehung angenommen:

(ID 13429)
In der Modellierung des Tiefenflusses sind vier Str mungen zu ber cksichtigen:
Der Hauptfluss $F_w$, der sich entlang des Meeresbodens bewegt.
Der Verlustfluss $F_i$, der aufgrund der Corioliskraft abgelenkt wird.
Der Auftriebsfluss $U_x$, der dem Anteil des Verlustflusses entspricht, der die Oberfl che erreicht.
Der Sinkfluss $S_0$, der aus den Oberfl chenstr mungen stammt und auch die zur ckgesunkenen Verluste einschlie t.

(ID 13425)
Die sogenannte Coriolis-Kraft spielt eine wesentliche Rolle in der Dynamik des Wassers an den Polen und beeinflusst, wie Wassermassen aufgrund von Temperatur- und Salinit tsunterschieden absteigen.

Bei der Analyse des Atlantischen Ozeans kann man eine Bewegung des Wassers vom Pol zum quator beobachten, die nach Westen abgelenkt wird. Dieses Ph nomen wird durch die Verz gerung im Vergleich zur Rotation des Planeten verursacht, wenn man von einer Zone geringerer Geschwindigkeit entlang der Breitengrade zu einer Zone h herer Geschwindigkeit bergeht. Dieses Verhalten kann mit der Coriolis-Gleichung f r die x-Richtung modelliert werden, die durch coriolis-Beschleunigung an der Oberfläche in x-Richtung $m/s^2$, coriolis-Faktor $rad/s$ und geschwindigkeit im Meridian $m/s$ gegeben ist:
| $ a_{c,x} = f v_y $ |
In dieser Gleichung ist der Coriolis-Faktor
Die geografische Kontur des Kontinents erm glicht eine Bewegung in der x-Richtung (L ngengrad), was zu einer Beschleunigung in der y-Richtung (Breitengrad) f hrt. Diese kann mit coriolis-Beschleunigung an der Oberfläche in y-Richtung $m/s^2$, coriolis-Faktor $rad/s$ und parallelgeschwindigkeit $m/s$ berechnet werden:
| $ a_{c,y} = - f v_x $ |
Diese Berechnung zeigt, dass in der N he des quators Verschiebungen auftreten, bei denen Wasser von der Hauptstr mung weg und nach Norden bewegt wird. Wenn wir die Beschleunigung in der z-Richtung (Tiefe) betrachten und ber cksichtigen, dass
| $ a_{cz} = R \beta v_x $ |
.
(ID 12122)
Am Ende l sen Stommel und Arons [1], [2] das Modell und zeigen die wichtigsten Tiefenstr mungen, die weltweit existieren:

[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. ( ber die abyssale Zirkulation des Weltmeeres - I. Station re planetare Str mungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. ( ber die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
(ID 12099)
Als Stommel und Arons [1], [2] ihr erstes Modell der thermohalinen Zirkulation entwickelten, unterteilten sie die verschiedenen Ozeane in Zonen mit definierter Auftriebsstr mung (nach oben zeigende Pfeile) und zwei Quellen, eine in der Arktis und eine andere in der Antarktis:

Globales Zirkulationsmodell in Sv (Sverdrup) ($10^6 m^3/s$) [2].
[1] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanI. Stationary planetary flow patterns on a sphere. ( ber die abyssale Zirkulation des Weltmeeres - I. Station re planetare Str mungsmuster auf einer Kugel.) Deep Sea Research (1953), 6(2), 140-154.[2] Stommel, H., & Arons, A. B. (1960). On the abyssal circulation of the world oceanII. An idealized model of the circulation pattern and amplitude in oceanic basins. ( ber die abyssale Zirkulation des Weltmeeres - II. Ein ideales Modell des Musters und der Amplitude der Zirkulation in ozeanischen Becken.) Deep Sea Research (1953), 6(3), 217-233.
(ID 12098)
Messungen haben gezeigt, dass die thermohaline Zirkulation ein integriertes System ist, das den gesamten Globus umspannt. Es gibt mindestens zwei Punkte, die als Quellen betrachtet werden k nnen, und ihr Verlauf erstreckt sich ber alle Ozeane.

(ID 12097)
Durch mehrere Simulationen werden die Auswirkungen der polaren Eisschmelze auf das Absinken und dessen Einfluss auf die Tiefenzirkulation untersucht. Es gibt Anzeichen daf r, dass die Zirkulation bereits r ckl ufig ist. Ein Zusammenbruch der Tiefenzirkulation bedeutet jedoch nicht zwangsl ufig dasselbe f r die Oberfl chenzirkulation, die durch Winde angetrieben wird. Was passieren k nnte, ist eine Verschiebung in der Oberfl chenzirkulation, was zu einer Verringerung des Beitrags des Golfstroms an warmem Wasser f r Nordeuropa f hrt.
Das folgende Diagramm zeigt Variationen im Fluss in Einheiten von Sv (Sverdrup), was etwa $10^6,m^3/s$ entspricht:

Unter der Annahme einer Absinkrate von etwa 20 Sv l sst sich schlussfolgern, dass in einigen Simulationen die Tiefenzirkulation zum Stillstand kommt. Diese Variationen sind mit verschiedenen zuk nftigen Szenarien menschlicher Aktivit ten und berlegungen zu Aspekten verbunden, bei denen es weniger Gewissheit ber ihr Eintreten gibt. Detailliertere Informationen finden sich in den Berichten des Intergovernmental Panel on Climate Change (IPCC).
(ID 13430)
(ID 15585)
ID:(1623, 0)
