Guía para el caso
Storyboard 
El caso busca que se logre interpretar una señal compleja de una medición de ultrasonido identificando el tipo de tejido y el año de las distintas capas de la muestra.
ID:(515, 0)
Generación de la señal a estudiar
Definición 
Como primer paso se debe ingresar al simulador para generar la señal que se va a estudiar. Una vez ingresado al simulador se ejecuta este con el botón simular tras lo cual en la pestaña 'gráfica':

En la imagen se observan lineas de color azul y rojas que corresponden a los ecos de una señal inicial de amplitud 1 en las distintas capas de la muestra. El objetivo del caso es lograr identificar los tipos de materiales y el grosor de las distintas capas.
Una vez generada la información se debe proceder a traspasar la información al caso lo que se hace oprimiendo el botón 'por defecto'. Una vez ejecutado dicho botón los datos para analizar no son modificados a menos que se borre el caso por completo.
ID:(4131, 0)
Datos a analizar en el caso
Imagen 
Una vez ejecutada la simulación y cargados los datos, estos reemplazan los campos en que hasta aquí se observaba una pequeña pantalla de computador:
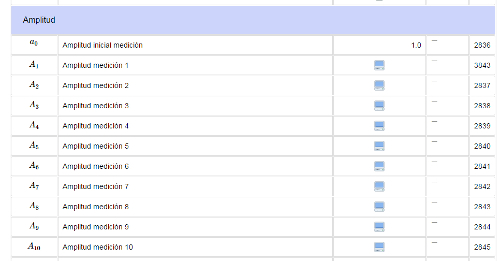
Existen dos grupos de datos,
- los tiempos, que corresponden a los valores de los picos rojos en el eje de las abscisas, y
- las amplitudes que corresponden a los valores en las ordenadas
Muchos de los picos de tiempos
ID:(4136, 0)
Ingreso de impedancias conocidas
Nota 
Tanto el primer como el ultimo, el quinto, medio son conocidos. En el primer caso se trata del gel que se usa como contacto entre el cuerpo y el transductor. El ultimo medio se asume como aire y corresponde a lo que esta detrás del objeto a estudiar. Los datos de estos medios se pueden obtener de la hoja 'Impedancias' del simulador:
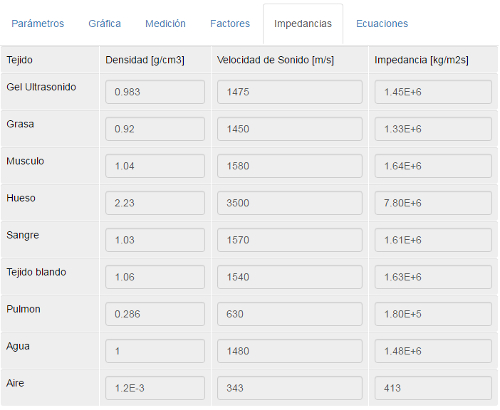
Los datos de densidad y velocidad de sonido deben ser ingresados manualmente al caso mientras que el valor de la impedancia debe ser calculado. La ecuación para el calculo de la impedancia se encuentra en la ultima pestaña del simulador.
ID:(9061, 0)
Determinar la impedancia de la capa en contacto con el gel
Cita 
La primera linea de la gráfica de la señal de ultrasonido presenta una amplitud que corresponde al reflejo en la interface entre el primer y segundo medio
con lo que se puede determinar el factor de reflexión. Una vez se ha calculado este valor se pude determinar la impedancia de la segunda capa ya que
Al determinar la impedancia
Una vez que se tiene la velocidad de sonido en el segundo medio es posible estimar el grosor de esta en función del correspondiente eco. En este caso el segundo pico de la señal de ultrasonido corresponde a este eco por lo que se puede directamente trabajar con
ID:(9062, 0)
Determinación de impedancias
Ejercicio 
En la medida que se logre trabajar solo con señales que sufren una única reflexión es posible estimar el factor de reflexión de la interface en que la onda es relejada. Para ello basta conocer la amplitud inicial, las impedancias de las capas que antecedan a la capa en que ocurre la reflexión y la amplitud que se mide en el transductor.
Un ejemplo es la medición del factor de reflexión en una tercera capa en que se conoce la impedancia de la primera
que despejando nos da el valor del factor de reflexión
Este proceso se puede realizar para cualquier número de capas ya que siempre se pueden calcular los respectivos factores de transmisión de las capas anteriores.
Una vez determinado el factor de resistencia se puede calcular la impedancia del medio en que se reflejo la onda sonora ya que
Una vez se ha reconocido por la impedancia el tipo de material que se esta observando se puede estimar la velocidad de propagación y con ello determinar el grosor de la capa.
ID:(4134, 0)
Problemática de los múltiples ecos
Ecuación 
Para estimar la impedancia de un medio es necesario poder reconocer la onda sonora que se reflejo en este. Un problema para lograr esto son los múltiples ecos que pueden ocurrir en las capas anteriores por las que cruza el haz.
Para evitar este problema se pueden usar los datos de las capas anteriores (grosor y velocidad del sonido) para estimar los posibles ecos y descartar de los ecos aquellos que provienen de ondas que han sufrido mutiples ecos.
El método es considerar cada uno de los posibles caminos. Si estos se describen indicando el número del medio y luego con un signo '+' si se viaja alejándose del transductor y '-' hacia este. De esta forma
la señal que atraviesa el gel (1+), se refleja y vuelve por el mismo medio (1-) sería
- 1+1-
En el caso de que la señal viaja por el primero (1+) y segundo medio (2+), se refleja y vuelve por el segundo (2-) y luego primer medio (1-) es
- 1+2+2-1-
Las próximas dos lineas mono-eco son en esta forma
- 1+2+3+3-2-1-
- 1+2+3+4+4-3-2-1-
Por ello el mecanismo de calculo en que se procede a
- reconocer el pico que corresponde a una señal de un solo eco (mono-eco)
- estimar la amplitud de la señal
- calcular la transmisión de la señal tanto de ida como vuelta atreves de las capas anteriores
- calcular el factor de reflexión de la interface
- calcular la impedancia de la próxima capa
- reconoce el medio y determina velocidad de sonido y la densidad
- calcular el grosor de la capa con la diferencia del tiempo de eco y la velocidad de sonido
Para determinar las lineas correcta y evitar lineas de múltiple eco el simulador genera la lista de tiempos, amplitudes y rutas en la pestaña 'medición'. En esta se deben identificar aquellas lineas que son de mono eco:

ID:(4135, 0)
Guía para el caso
Storyboard 
El caso busca que se logre interpretar una señal compleja de una medición de ultrasonido identificando el tipo de tejido y el año de las distintas capas de la muestra.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Como primer paso se debe ingresar al simulador para generar la se al que se va a estudiar. Una vez ingresado al simulador se ejecuta este con el bot n simular tras lo cual en la pesta a 'gr fica':
En la imagen se observan lineas de color azul y rojas que corresponden a los ecos de una se al inicial de amplitud 1 en las distintas capas de la muestra. El objetivo del caso es lograr identificar los tipos de materiales y el grosor de las distintas capas.
Una vez generada la informaci n se debe proceder a traspasar la informaci n al caso lo que se hace oprimiendo el bot n 'por defecto'. Una vez ejecutado dicho bot n los datos para analizar no son modificados a menos que se borre el caso por completo.
Una vez ejecutada la simulaci n y cargados los datos, estos reemplazan los campos en que hasta aqu se observaba una peque a pantalla de computador:
Existen dos grupos de datos,
- los tiempos, que corresponden a los valores de los picos rojos en el eje de las abscisas, y
- las amplitudes que corresponden a los valores en las ordenadas
Muchos de los picos de tiempos
Tanto el primer como el ultimo, el quinto, medio son conocidos. En el primer caso se trata del gel que se usa como contacto entre el cuerpo y el transductor. El ultimo medio se asume como aire y corresponde a lo que esta detr s del objeto a estudiar. Los datos de estos medios se pueden obtener de la hoja 'Impedancias' del simulador:
Los datos de densidad y velocidad de sonido deben ser ingresados manualmente al caso mientras que el valor de la impedancia debe ser calculado. La ecuaci n para el calculo de la impedancia se encuentra en la ultima pesta a del simulador.
El primer paso en el an lisis es aprovechar el conocimiento de las propiedades de la primera capa para determinar su grosor. Esto se puede dado que se conoce tanto la velocidad de sonido en el medio como el tiempo de eco que se observa como el primer pico de la gr fica de la se al ultrasonido.
Si la onda sonora viaja con una velocidad
La se al recibida despu s del tiempo
El factor 2 se debe a que el sonido recorre dos veces la distancia
La primera linea de la gr fica de la se al de ultrasonido presenta una amplitud que corresponde al reflejo en la interface entre el primer y segundo medio
con lo que se puede determinar el factor de reflexi n. Una vez se ha calculado este valor se pude determinar la impedancia de la segunda capa ya que
Al determinar la impedancia
Una vez que se tiene la velocidad de sonido en el segundo medio es posible estimar el grosor de esta en funci n del correspondiente eco. En este caso el segundo pico de la se al de ultrasonido corresponde a este eco por lo que se puede directamente trabajar con
Si la onda sonora viaja por la
Esto es solo valido en la medida que tanto el tiempo de eco
En la medida que se logre trabajar solo con se ales que sufren una nica reflexi n es posible estimar el factor de reflexi n de la interface en que la onda es relejada. Para ello basta conocer la amplitud inicial, las impedancias de las capas que antecedan a la capa en que ocurre la reflexi n y la amplitud que se mide en el transductor.
Un ejemplo es la medici n del factor de reflexi n en una tercera capa en que se conoce la impedancia de la primera
que despejando nos da el valor del factor de reflexi n
Este proceso se puede realizar para cualquier n mero de capas ya que siempre se pueden calcular los respectivos factores de transmisi n de las capas anteriores.
Una vez determinado el factor de resistencia se puede calcular la impedancia del medio en que se reflejo la onda sonora ya que
Una vez se ha reconocido por la impedancia el tipo de material que se esta observando se puede estimar la velocidad de propagaci n y con ello determinar el grosor de la capa.
Para estimar la impedancia de un medio es necesario poder reconocer la onda sonora que se reflejo en este. Un problema para lograr esto son los m ltiples ecos que pueden ocurrir en las capas anteriores por las que cruza el haz.
Para evitar este problema se pueden usar los datos de las capas anteriores (grosor y velocidad del sonido) para estimar los posibles ecos y descartar de los ecos aquellos que provienen de ondas que han sufrido mutiples ecos.
El m todo es considerar cada uno de los posibles caminos. Si estos se describen indicando el n mero del medio y luego con un signo '+' si se viaja alej ndose del transductor y '-' hacia este. De esta forma
la se al que atraviesa el gel (1+), se refleja y vuelve por el mismo medio (1-) ser a
- 1+1-
En el caso de que la se al viaja por el primero (1+) y segundo medio (2+), se refleja y vuelve por el segundo (2-) y luego primer medio (1-) es
- 1+2+2-1-
Las pr ximas dos lineas mono-eco son en esta forma
- 1+2+3+3-2-1-
- 1+2+3+4+4-3-2-1-
Por ello el mecanismo de calculo en que se procede a
- reconocer el pico que corresponde a una se al de un solo eco (mono-eco)
- estimar la amplitud de la se al
- calcular la transmisi n de la se al tanto de ida como vuelta atreves de las capas anteriores
- calcular el factor de reflexi n de la interface
- calcular la impedancia de la pr xima capa
- reconoce el medio y determina velocidad de sonido y la densidad
- calcular el grosor de la capa con la diferencia del tiempo de eco y la velocidad de sonido
Para determinar las lineas correcta y evitar lineas de m ltiple eco el simulador genera la lista de tiempos, amplitudes y rutas en la pesta a 'medici n'. En esta se deben identificar aquellas lineas que son de mono eco:
Si el pulso se refleja en la interface entre el segundo y el tercer medio el pulso:
es transmitido del medio
es reflejado en el interface entre el medio
es transmitido del medio
el factor de reflexi n del sistema es:
reflejo y transmisi n.
Si el pulso se refleja en la interface entre el segundo y el tercer medio el pulso:
es transmitido del medio
es reflejado en el interface entre el medio
es transmitido del medio
el factor de reflexi n del sistema es en funci n de las impedancias
reflejo y transmisi n.
Si el pulso se refleja en la interface entre el tercero y el cuarto medio el pulso:
es transmitido del medio
es transmitido del medio
es reflejado en el interface entre el medio
es transmitido del medio
es transmitido del medio
el factor de reflexi n del sistema es:
reflejo y transmisi n
Si el pulso se refleja en la interface entre el tercer y el cuarto medio el pulso:
es transmitido del medio
es transmitido del medio
es reflejado en el interface entre el medio
es transmitido del medio
es transmitido del medio
el factor de reflexi n del sistema es en funci n de las impedancias
reflejo y transmisi n
Si el pulso se refleja en la interface entre el cuarto y el quinto medio el pulso:
es transmitido del medio
es transmitido del medio
es transmitido del medio
es reflejado en el interface entre el medio
es transmitido del medio
es transmitido del medio
es transmitido del medio
el factor de reflexi n del sistema es:
reflejo y transmisi n
Si el pulso se refleja en la interface entre el cuarto y el quinto medio el pulso:
es transmitido del medio
es transmitido del medio
es transmitido del medio
es reflejado en el interface entre el medio
es transmitido del medio
es transmitido del medio
es transmitido del medio
el factor de reflexi n del sistema es en funci n de las impedancias
reflejo y transmisi n
ID:(515, 0)
