Nos basamos en el modelo de 24 compartimientos. Los Q representan el flujo sangu neo y se miden en ml/min. Salvo excepciones indicadas, el indice indica el compartimiento del que procede. El n mero en los compartimiento indica el volumen en ml de estos.

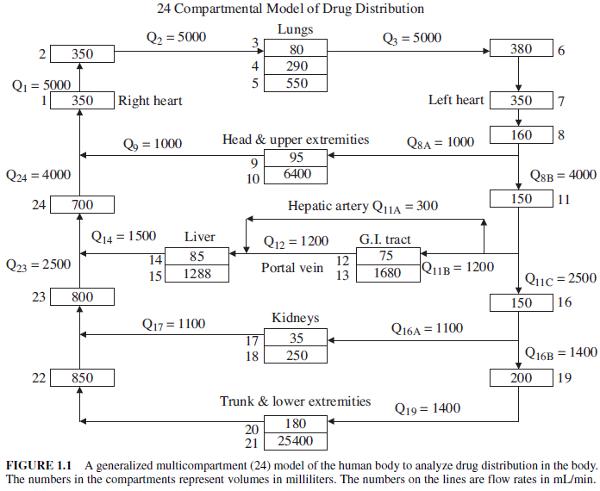
Los compartimientos que est n dentro del flujo corresponden a arterias y venas mientras que los compartimientos adyacentes a la red de capilares. Estos ltimos act an mas bien como elementos que son capaces de difundir el f rmaco desde o hacia el torrente sanguino. Por este motivo los describiremos como 'difusores'.

Notas: El significado de cada compartimiento se listan en la pr xima p gina. Los valores Indicados en la imagen no corresponden a los valores que tiene cada caso.

(ID 906)

Lo segundo a definir los los flujos en los distintos segmentos entre vol menes. En la mayor a se observa el flujo del torrente sangu neo (5 ltrs/min) mientras que en algunas partes se observan bifurcaciones o concentraciones. Dichos valores deben ser determinados de modo de que el volumen de la sangre se conserve, es decir se mantenga constante por todo el sistema.

(ID 907)

Las constantes de difusi n entre vol menes $K$ y hacia afuera del sistema $R$ se pueden estimar en base al articulo 'The Permeability of Capillaries in Various Organs as Determined by Use of the 'Indicator Diffusion' Method' de Christian Crone aparecido en el Acta Physiologica Scandinavica, 1963, Vol 58, p g. 292-305. Para ello deben localizarse las curvas de concentraci n por rgano y estimar el tiempo en que estas bajan a la mitad. El inverso de estos tiempos es del orden de las constantes de difusi n del mas interfaces entre vol menes y exterior.

Al existir varias constantes se puede asumir para la primera dicho valor y para las dem s valores tal que le sea mas f cil difundir. De esta forma sera la primera interfaces la que caracteriza la permeabilidad. As tampoco se debiesen dar flujos inversos, es decir desde afuera hacia adentro.

Nota: no use los valores incluidos en el simulador, estime sus propios valores indicando en la validaci n para que tipo de sustancia aplican (ver paper).

(ID 919)

Para modelar la dosis se debe determinar el volumen y el tiempo durante el cual se administrara.

Con el volumen total del f rmaco y el volumen de la sangre que circula se puede determinar la concentraci n promedio que llegar a a existir en la medida que no difunda hacia afuera el f rmaco.

Adicionalmente se pide estimar, en base a la simulaci n el valor m ximo de la concentraci n que llego a existir en el volumen en que se aplico la dosis. Este es mayor al valor medio por el hecho que el f rmaco administrado se desplaza inicialmente en forma concentrada y solo a media que va siendo fraccionado por las bifurcaciones se homogeneiza llegando a una distribuci n mas pareja.

(ID 908)

En el caso del intestino e h gado la estructura es mas compleja. Por ello se debe primero determinar la fracci n que termina yendo directo al h gado. Esto se logra estimando el volumen total que sale de intestino, que es igual a lo que llega menos lo que se difunde S_{12}-S_{13} y rest ndoselo al total que llega al h gado que es S_{14}:

(ID 2045)

En cada elemento se considera tanto el flujo que ingresa como el que sale. Esto puede llevar a que, fuera de que una cantidad ingrese multiples veces via la circulaci n, existan flujos en la direcci n inversa. Esto dificulta poder estimar el real flujo por las distintas bifurcaciones.

Sin embargo, como se puede tomar un tiempo suficientemente largo, se puede estimar el total que termina ingresando a cada elemento con lo que se pueden establecer relaciones de proporcionalidad. Si se estima el flujo que ingresa a un elemento como el flujo de sangre Q_i que sale de los elementos con concentraci n c_i anteriores al elemento en estudio se tendr que ser

s=\sum_ic_iQ_i

Por ello el total del f rmaco que entre a uno de los volumen es

S(t)=\sum_i\int_0^{t}dt'Q_ic_i(t')

Como el flujo de la sangre se puede suponer como constante se tiene finalmente que el ingreso total de f rmaco a un volumen es

Para obtener el total que ingreso basta considerar un tiempo suficientemente largo. Hay que tener presente que en general este volumen tambi n abandona el elemento, o sea no puede ser usado para estimar concentraciones que existieron en este.

(ID 3043)

En el caso del difusor se introduce la constante K que multiplicada por el volumen de origen V permite conocer con la concentraci n C el flujo que entra a uno de estos elementos

s(t)=KVC(t)

Al integrar en el tiempo se obtiene en el lado izquierdo el volumen del f rmaco en el difusor mientras que en el lado derecho un valor proporcional al volumen de f rmaco que entra al volumen que antecede. Por ello se tiene que

S=KVS_0

o sea que

(ID 9088)

Como la suma de f rmaco que ingresa a un volumen S_i es proporcional al flujo sangu neo Q_i que ingresa a este y como se conoce el flujo que ingresa a la bifurcaci n es Q se puede por continuidad asumir que

(ID 9085)

En caso de que la bifurcaci n sea a dos elementos, la ecuaci n general

se reduce a

(ID 9086)

En caso de que la bifurcaci n sea a tres elementos, la ecuaci n general

se reduce a

(ID 9087)

El siguiente es el simulador del sistema de circulaci n en que se puede introducir un f rmaco y observar como se distribuye:

(ID 9734)

La p gina flujo del simulador entrega los datos definidos al resolver el caso:

(ID 9735)

La p gina flujo del simulador entrega los volumenes definidos al resolver el caso:

(ID 9736)

La p gina flujo del simulador entrega las cantidades definidos al resolver el caso:

(ID 9737)

La p gina flujo del simulador entrega las gr ficas G1 definidos al resolver el caso:

(ID 9738)

La p gina flujo del simulador entrega las gr ficas G2 definidos al resolver el caso:

(ID 9739)

La p gina flujo del simulador entrega las gr ficas G3 definidos al resolver el caso:

(ID 9740)

La p gina flujo del simulador entrega las gr ficas G4 definidos al resolver el caso:

(ID 9741)

La p gina flujo del simulador entrega las gr ficas G5 definidos al resolver el caso:

(ID 9742)

La p gina flujo del simulador entrega las gr ficas G6 definidos al resolver el caso:

(ID 9743)