Aufbau des Ohrs
Bild 
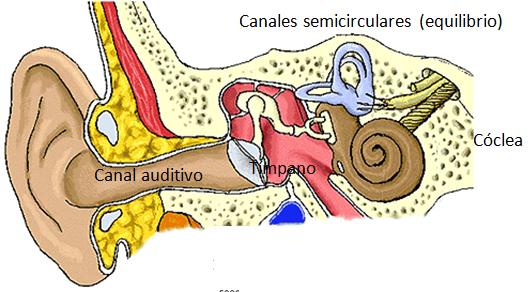
El oído está conformado por el canal auditivo, el tímpano, el yunque y la cóclea. El canal permite que el sonido alcance el tímpano que es una membrana capaz de oscilar y traspasar el movimiento amplificado por el yunque hasta la cloquea. Esta última funciona como un analizador de frecuencias que reporta al celebró la estructura del sonido recepcionado.
ID:(1674, 0)
Struktur der Coclea
Zitat 
La cóclea tiene la forma de un caracol que se vuelve cada vez mas estrecho. Consta de dos cámaras separadas por una membrana que se extienden por todo el largo de la cóclea. El sonido penetra por el canal y la membrana entra en resonancia en una profundidad que depende del largo de onda. De esta forma se desglosa la señal en sus componentes según la frecuencia.

ID:(1866, 0)
Höhr Kapazität des menschlichen Ohres
Gleichung 
El oído humano puede captar sonidos con frecuencias entre 20 Hz y 20 kHz. Dicha capacidad se documenta con el numero de decibeles que se amortigua el sonido por frequencia:

De la gráfica se ve que la menor amortiguación es entre 200 Hz y 8 kHz.
ID:(1874, 0)
Capacidad de Escuchar
Beschreibung 
Variablen
Berechnungen
Berechnungen
Gleichungen
(ID 3408)
Beispiele
(ID 514)
El o do est conformado por el canal auditivo, el t mpano, el yunque y la c clea. El canal permite que el sonido alcance el t mpano que es una membrana capaz de oscilar y traspasar el movimiento amplificado por el yunque hasta la cloquea. Esta ltima funciona como un analizador de frecuencias que reporta al celebr la estructura del sonido recepcionado.

(ID 1674)
(ID 538)
La c clea tiene la forma de un caracol que se vuelve cada vez mas estrecho. Consta de dos c maras separadas por una membrana que se extienden por todo el largo de la c clea. El sonido penetra por el canal y la membrana entra en resonancia en una profundidad que depende del largo de onda. De esta forma se desglosa la se al en sus componentes seg n la frecuencia.

(ID 1866)
(ID 1867)
$v_2=fv_1$
(ID 3408)
El o do humano puede captar sonidos con frecuencias entre 20 Hz y 20 kHz. Dicha capacidad se documenta con el numero de decibeles que se amortigua el sonido por frequencia:

De la gr fica se ve que la menor amortiguaci n es entre 200 Hz y 8 kHz.
(ID 1874)
Wie in anderen menschlichen Wahrnehmungssystemen ist unser Geh r in der Lage, Druckschwankungen in einem weiten Bereich wahrzunehmen $(10^{-5}-10^2 Pa)$. Wenn wir jedoch ein Signal verdoppeln, entspricht dies nicht dem doppelten Druck oder Schallintensit t, sondern vielmehr dem Quadrat dieser Gr en. Mit anderen Worten: Unsere F higkeit, Signale wahrzunehmen, arbeitet auf einer logarithmischen und nichtlinearen Skala.
Daher wird der Geräuschpegel ($L$) nicht in die Schallintensität ($I$) oder die Referenz Intensity ($I_{ref}$) angegeben, sondern im Zehnerlogarithmus dieser Gr en. Insbesondere nehmen wir die niedrigste Schallintensit t wahr, die wir wahrnehmen k nnen, die Referenz Intensity ($I_{ref}$)
, und verwenden sie als Referenz. Die neue Skala wird mit wie folgt definiert:
| $ L = 10 log_{10}\left(\displaystyle\frac{ I }{ I_{ref} }\right)$ |
(ID 3194)
Der Geräuschpegel ($L$) umfasst einen weiten Bereich von die Schalldruck ($p_s$), was es sinnvoll macht, eine Skala zu definieren, die diese Schwierigkeit mildert. Daf r k nnen wir mit dem Logarithmus des Drucks arbeiten, der durch einen Wert normalisiert ist, der null auf dieser Skala entspricht. Wenn wir den minimalen Druck nehmen, den eine Person wahrnehmen kann, definiert als die Referenzdruck ($p_{ref}$), k nnen wir eine Skala definieren mittels:
| $ L = 20 \log_{10}\left(\displaystyle\frac{ p_s }{ p_{ref} }\right)$ |
die im h rbaren Bereich bei 0 beginnt. Im Fall von Luft betr gt die Referenzdruck ($p_{ref}$) $20 \mu Pa$.
(ID 3407)
Der Schalldruck, den wir mit unserem Ohr wahrnehmen k nnen und der mit die Referenzdruck, Wasser ($p_{ref}$) bezeichnet wird, betr gt $2 \times 10^{-5} , Pa$.
Da die Schallintensität ($I$) mit die Schalldruck ($p_s$), die Mittlere Dichte ($\rho$) und die Speed of Sound ($c$) gleich ist
| $ I =\displaystyle\frac{ p ^2}{2 \rho c }$ |
kann ein Wert von die Referenz Intensity ($I_{ref}$) basierend auf dem Wert von die Referenzdruck, Wasser ($p_{ref}$) berechnet werden:
| $ I_{ref} =\displaystyle\frac{ p_{ref} ^2}{2 \rho c }$ |
Dies wird mit einer Dichte von $1.27 , kg/m^3$ und einer Schallgeschwindigkeit von $331 , m/s$ erreicht, was $9.5 \times 10^{-13} , W/m^2$ entspricht.
(ID 3409)
$L=L_0 -40\log_{10}\left(\displaystyle\frac{r}{r_0}\right)$
(ID 3410)
(ID 133)
ID:(303, 0)
