Forma de propagación de sonido en un teatro
Definición 
En el diseño del teatro se implementan distintas medidas de reflexión y de absorción de modo de lograr una acústica amplificando con la estructura misma:

ID:(1868, 0)
Intensidad sonora en la recepción
Imagen 
Como conocemos las distancias podemos calcular con que intensidad sonora llega el sonido directo
Con esta información podemos calcular la intensidad total que esta captando el receptor
ID:(537, 0)
Intensidad sonora de la cantante
Nota 
El sonido se desplaza por la laringe llegando a ser emitido de la boca con una intensidad similar a la que se origina a la altura de las cuerdas vocales
La intensidad total
ID:(535, 0)
Propagación del sonido en el auditorio
Ejercicio 
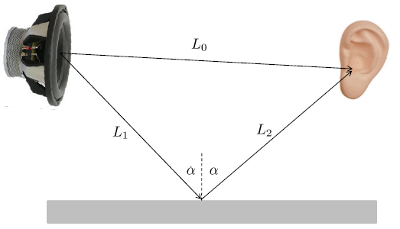
Una vez el sonido es emitido puede recorrer varios caminos hasta el auditor.

Por un lado está el haz directo, cuya distancia recorrida se puede calcular de la distancia horizontal y diferencia de la aturas entre cantante y receptor.
Existe una segunda contribución vía el techo que se encuentra a una altura sobre la cantante. En este caso es necesario determinar el punto en que se refleja el sonido en el techo.
Algo similar ocurre con el sonido reflejado en la pared detrás de la cantante. En este caso es necesario conocer la distancia entre cantante y pared y también determinar donde se refleja el sonido.
Con los tres caminos podemos calcular con qué desfase de tiempo llega el sonido al receptor y así asegurar que no se está produciendo eco.
ID:(536, 0)
Acustica de Salas
Storyboard 
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
En el dise o del teatro se implementan distintas medidas de reflexi n y de absorci n de modo de lograr una ac stica amplificando con la estructura misma:
Si conocemos la distancia entre fuente y receptor en forma directa
donde
Si se asume una velocidad del sonido de
Si el sonido viaja una distancia en la horizontal
Como conocemos las distancias podemos calcular con que intensidad sonora llega el sonido directo
Con esta informaci n podemos calcular la intensidad total que esta captando el receptor
Si
En un intervalo de tiempo
El sonido se desplaza por la laringe llegando a ser emitido de la boca con una intensidad similar a la que se origina a la altura de las cuerdas vocales
La intensidad total
Formaci n de eco
Si el sonido viaja una distancia inicial
Una vez el sonido es emitido puede recorrer varios caminos hasta el auditor.
Por un lado est el haz directo, cuya distancia recorrida se puede calcular de la distancia horizontal y diferencia de la aturas entre cantante y receptor.
Existe una segunda contribuci n v a el techo que se encuentra a una altura sobre la cantante. En este caso es necesario determinar el punto en que se refleja el sonido en el techo.
Algo similar ocurre con el sonido reflejado en la pared detr s de la cantante. En este caso es necesario conocer la distancia entre cantante y pared y tambi n determinar donde se refleja el sonido.
Con los tres caminos podemos calcular con qu desfase de tiempo llega el sonido al receptor y as asegurar que no se est produciendo eco.
El coeficiente de absorci n de paredes se calcula como el promedio ponderado de los coeficientes de absorci n de cada tipo de pared multiplicado por la fracci n de pared de este tipo:
Los coeficientes de los distintos tipos de elementos son funciones de las frecuencias y se resumen a continuaci n:
Elementos | 125 Hz | 250 Hz | 500 Hz | 1000 Hz | 2000 Hz | 4000 Hz
:---------------|:-----:|:-----:|:-----:|:-----:|:-----:|:-----:
Enyesado liso en mamposter a u hormig n | 0.01 | 0.01 | 0.02 | 0.02 | 0.03 | 0.04
Suspendido placas de yeso lisas | 0.25 | 0.20 | 0.10 | 0.05 | 0.05 | 0.10
Paneles de pared de madera o tableros de fibra de listones | 0.40 | 0.30 | 0.20 | 0.10 | 0.10 | 0.20
Pisos cobertor encolado | 0.02 | 0.03 | 0.04 | 0.05 | 0.05 | 0.10
Parqu , etc. en subsuelo | 0.20 | 0.15 | 0.10 | 0.10 | 0.05 | 0.10
Alfombras de espesor medio | 0.05 | 0.08 | 0.20 | 0.30 | 0.35 | 0.40
Cortinas | 0.10 | 0.15 | 0.30 | 0.40 | 0.50 | 0.60
Panel ac stico, 2 cm pegados | 0.10 | 0.15 | 0.40 | 0.60 | 0.70 | 0.70
Panel ac stico, de 2 cm, de rejilla | 0.20 | 0.30 | 0.60 | 0.70 | 0.70 | 0.70
Ventana cerrada | 0.10 | 0.04 | 0.04 | 0.02 | 0.02 | 0.02
Con los oyentes, orquestas, coros rea ocupada | 0.60 | 0.74 | 0.88 | 0.96 | 0.93 | 0.85
rea del asiento (tapizado con funda de tela) sin oyentes | 0.49 | 0.66 | 0.80 | 0.88 | 0.82 | 0.70
rea del asiento (tapizados con cuero) sin oyentes | 0.44 | 0.54 | 0.60 | 0.62 | 0.58 | 0.50
Audiencia (/ persona m2) de pie o en sillas de madera | 0.15 | 0.30 | 0.50 | 0.55 | 0.60 | 0.50
Audiencia (/ persona m2) de pie o en asientos tapizados | 0.20 | 0.40 | 0.55 | 0.60 | 0.60 | 0.50
Orquesta con instrumentos en el podio / persona | 0.40 | 0.80 | 1.00 | 1.40 | 1.30 | 1.20
Madera de estar solos | 0.01 | 0.01 | 0.02 | 0.03 | 0.05 | 0.05
De asientos tapizados solas con revestimiento de tela | 0.10 | 0.30 | 0.35 | 0.45 | 0.50 | 0.40
De estar solo tapizados con cuero | 0.10 | 0.25 | 0.35 | 0.35 | 0.20 | 0.10
ID:(306, 0)