Modelos Epidemiológicos
Imagen 
Un ejemplo en que se puede estudiar como se desarrollan modelos matemáticos son los modelos epidemiológicos del tipo SIR (susceptibles - infectados - recuperados).

ID:(8142, 0)
Modelo de Infección
Imagen 
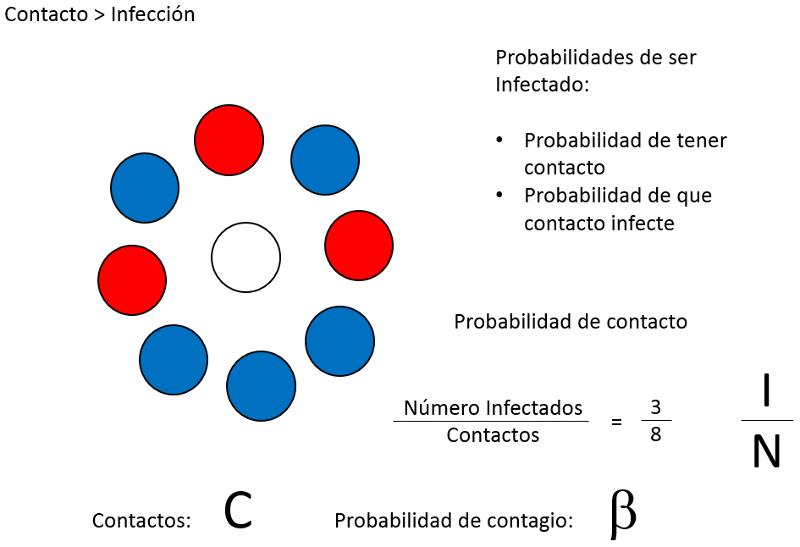
Para modelar el proceso de infección de una persona se debe primero estimar el numero de contactos que este tiene (C). Después se debe estimar la probabilidad que alguno de estos este infectado lo que se calcula como el número de infectados por el número de personas (I/N). Finalmente debe considerarse la probabilidad de que por unidad de tiempo el contacto lleve realmente a un contagio (\beta):
ID:(8143, 0)
Tasa de Contagio
Imagen 
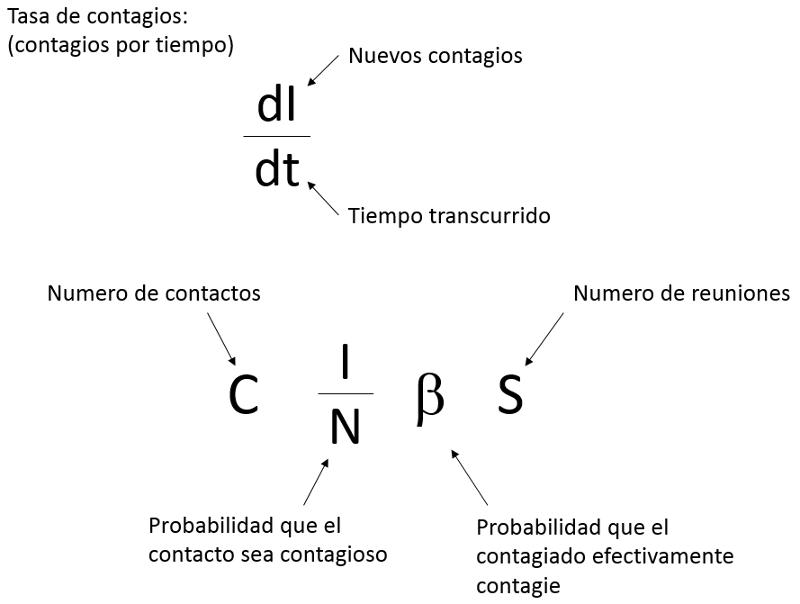
Para calcular la tasa con que se infectan las personas, debemos multiplicar el numero medio de personas que se relacionan (C), por la probabilidad de que uno de estos este infectado (I/N), la probabilidad de que el contacto con un infectado lleve a la infección (\beta) y el numero de sanos (S).
ID:(8144, 0)
Ecuación y su Análisis
Imagen 
Una vez estimada la tasa de infección sabemos como el numero de estos se incrementara. Sin embargo existe la posibilidad de que los infectados se recuperen o mueran lo que va a llevar a una reducción. Por ello debemos considerar fuera del incremento por contagio la reducción por recuperación/muerte que debe ser proporcional al numero de infectados:
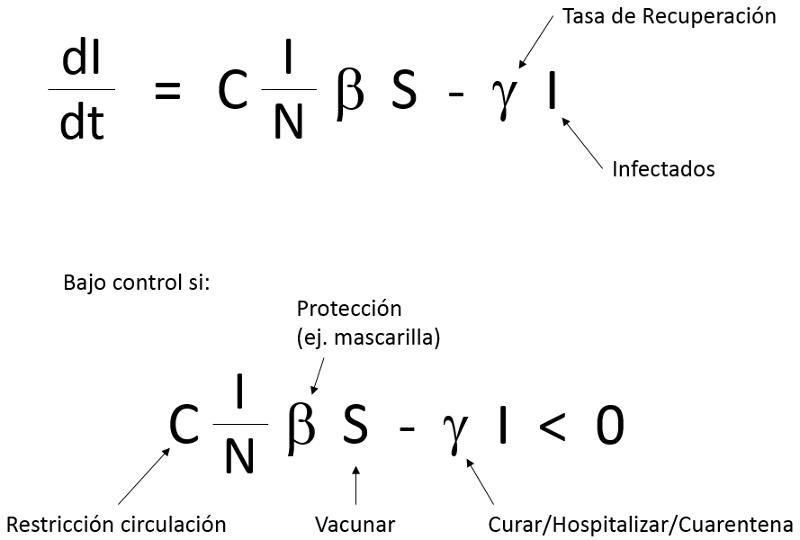
Como una tasa positiva significa que la enfermedad se esta propagando mientras que si es negativa se resta reduciendo se debe lograr que el lado derecho de la ecuación sea menor que cero.
Para modificar la situación y lograr esto, la ecuación nos indica que se debe:
* reducir los contactos C, lo que se puede hacer restringiendo la circulación de las personas
* reducir la probabilidad de contagio si llega a existir contacto \beta, lo que se puede hacer por ejemplo (según el tipo de enfermedad) con mascarillas, condones u otras protecciones
* reducir los susceptibles S, lo que se puede hacer con vacunación preventiva
* aumentar el retiro de infectados \gamma, lo que se puede hacer curando, hospitalizando o poniendo en cuarentena
ID:(8145, 0)
Simulador de Contagios
Html 
El modelo tipo SIR tiene finalmente tres ecuaciones, una para los susceptibles S,
\displaystyle\frac{dS}{dt}=-\beta C \displaystyle\frac{I}{N}S
otra para los infectados
\displaystyle\frac{dI}{dt}=\beta C\left(\displaystyle\frac{S}{N}-\displaystyle\frac{\gamma}{\beta C}\right)I
y una ultima para los recuperados
\displaystyle\frac{dR}{dt}=\gamma I
lo que permite estructurar un simulador.
ID:(8146, 0)
Simulador de Propagación
Html 
Modelos simples de propagación se pueden desarrollar en base a definir una red de contactos. Sobre esta red de marca una persona inicial (punto rojo) y este comienza a contagiar con una probabilidad p a sus vecinos.
Según se seleccione un valor para la probabilidad p las redes son o pequeñas o de un tamaño no menor. El limite esta en este caso en que la probabilidad de contagio sea inferior (redes pequeñas limitadas) o mayor (redes que pueden ser bastante grandes) a 1/2.
ID:(8147, 0)
Criticidad del Efecto
Imagen 
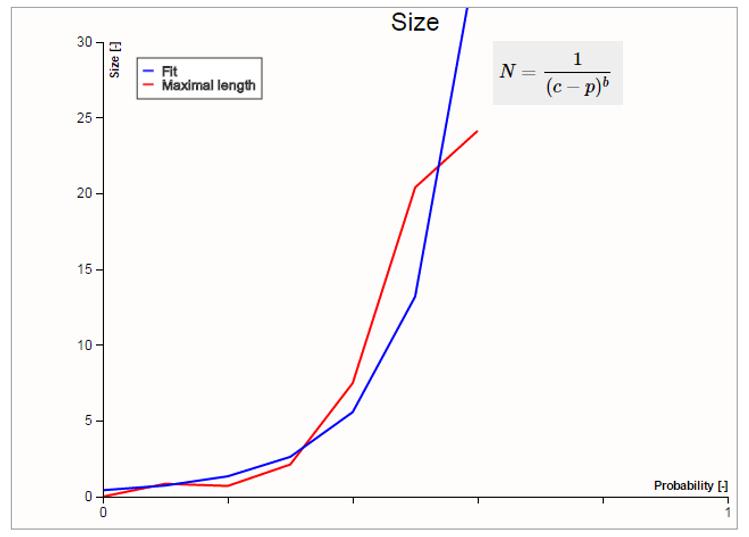
El efecto es bastante dramático. Si se calcula el radio medio que alcanza la figura según la probabilidad p. Si el valor es menor a 1/2 la tendencia es de tener redes pequeñas y acotadas. Si el valor es superior a p tienden a ser extendidas pudiendo llegar a ser infinitas.
ID:(8148, 0)
