La Otra Física: métodos
Storyboard 
Para entender mejor como se trabaja se explica como se aplica a un tema de actualidad como lo es el COVID19 (nota coronavirus es una familia de virus, COVID19 es un coronavirus en particular que se presento a fines de 2019). Se explica como se
• obtiene la información,
• como se forman modelos,
• usa modelos ya existente,
• adecua los modelos a la situación
• analizar los problemas con los datos que se pueden obtener
• adecuar modelo para usar datos con problemas
• calcular factores claves del modelo
• integrar comportamiento de personas y autoridades
• usar el modelos para buscar mejor estrategia
ID:(1604, 0)
Un caso práctico: Covid19
Imagen 
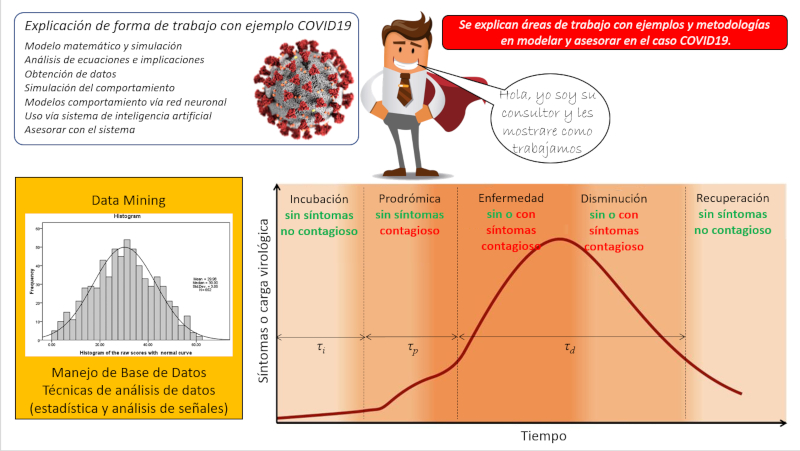
Para mostrar como se trabaja en esta otra física se muestra en forma simplificada como se estructura un modelo para estudiar la pandemia del COVID19 y como el trabajo se usa para asesorar en la toma de decisiones. También se explica las dificultades que se van teniendo y como estas se pueden ir abordando.
ID:(11929, 0)
Documentación COVID19
Video 
El siguiente video muestra como el virus se contagia, como penetra en la célula y como se replica para volver atacar otras células.
Datos para modelar se pueden obtener de:
Datos generales a nivel mundial sobre infectados, muertos, tests, medidas, etc.
Datos de Chile (MINSAL)
Datos por estado y comuna en Estados Unidos:
Datos de movilidad de Google:
COVID-19 Community Mobility Reports
ID:(11945, 0)
Construir un modelo
Imagen 
El primer paso es conocer el tema mediante
• leer información genérica para tener una visión general
• contactar expertos que pueden contribuir a una primera visión del tema
• busca de información mas detallada en los temas claves para el modelo
• buscar modelos existentes
• generar un modelo propio que cumple los requisitos de la información a obtener
• revisar el modelo con expertos que pueden señalar posibles errores conceptuales y/o de parámetros
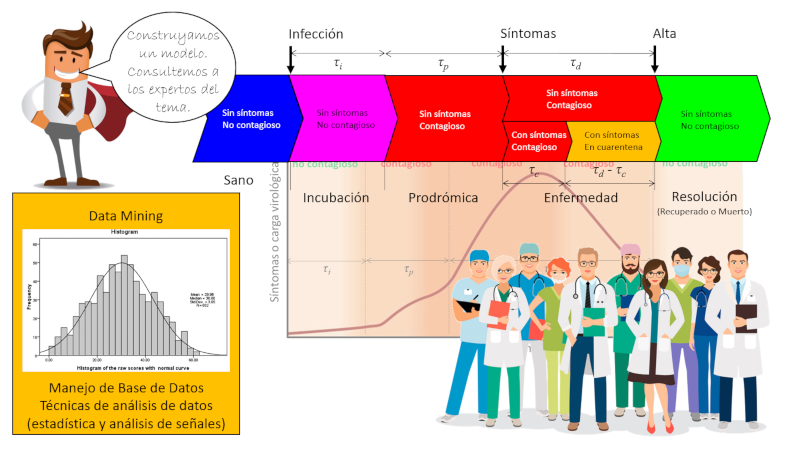
En este caso en particular existen dos temas claves que se deben modelar:
• los tiempos que demoran las distintas faces y la posibilidad de que la persona pueda contagiar a otros
• los mecanismos y la probabilidad de contagio por día
ID:(11930, 0)
Mecanismo de contagio
Imagen 
En el caso del COVID19 el principal contagio es por droplets (gotas que llevan el virus) que son expulsadas por el contagiado. Dependiendo del tamaño de las gotas estas caen a diferente velocidad al suelo. Esto se puede modelar con la ley de Stokes para el desplazamiento de esferas en un medio viscoso siendo la velocidad asintótica (la máxima que alcanza al caer) igual a\\n\\n
v=\displaystyle\frac{2\rho}{9\eta}a^2
donde
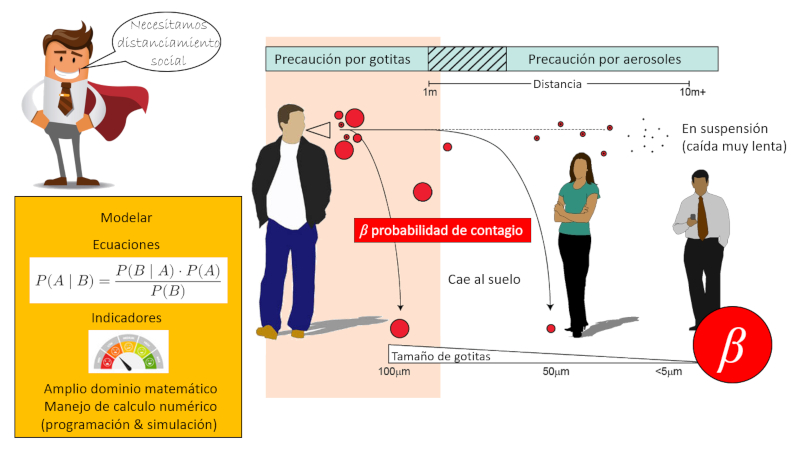
Si se asume que la gota es expulsada a una altura de 1.5 m se puede calcular con la velocidad de caída el tiempo de caída. Con una velocidad de expulsión de las gotas de 0.1 m/s y el tiempo de caída se puede calcular el alcance si no existieran procesos de difusión. Como si existe difusión se puede asumir que los rangos de gotas chicas están totalmente sobrestimados.
Si se consultan la literatura se vera que los droplets que se generan al hablar están entre 2 y 100 um con una mayor concentración entre 4 y 8 um (The size and the duration of air-carriage of respiratory droplets and droplet-nuclei, J. P. Duguid, J. Hyg. (Lond.) 44, 471-479 (1946)). Por ello las recomendaciones actuales de 1 metro son demasiado limitadas. Si se estudia con mayor detalle se vera que los droplets pasan a un modo de difusión que es de un rango mas limitado que el indicado. Por ello asumir una distancia de 2 metros es mas realista y se considerar que el las gotas permanecen varios minutos e incluso horas en el aire.
ID:(11931, 0)
Prevención de contagio
Imagen 
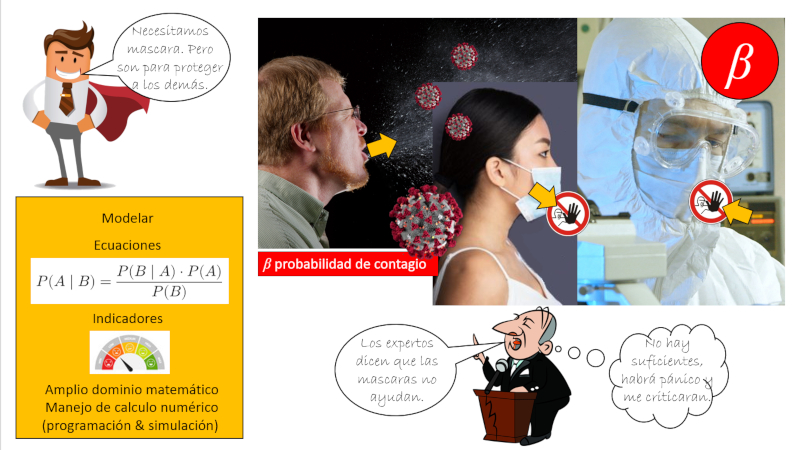
Al ver lo limitado que es el uso del distanciamiento social el uso de mascarilla se vuelve clave. Las mascarillas comunes capta una buena parte de los droplets emitidos por el portador de la mascara y por ello son una protección para los demás y no para el portador de la mascara. Como la porosidad no es menor no protegen contra aspirar droplets que ya estan en el ambiente.
Si se necesita una protección real debe usar una mascara del tipo N95 que tiene poros de un tamaño entre 65-125nm y por ello deja pasar solo pocos droplets. Por otro lado existe el peligro que los droplets alcancen alguna de las mucosas (zonas húmedas) del cuerpo por lo que es útil un protector para ojos (visor). Ademas se exige no tocarse boca, nariz o ojos ya que se pueden tener viruses en las manos y de esta forma llegar a mucosas. Personal en hospital ademas usa trajes de modo de que no se queden viruses adheridos a la vestimenta. Por ultimo esta el lavado que requiere de unos 20 segundos para que los jabone logren disolver la capa externa del virus y con ello destruirlo.
ID:(11932, 0)
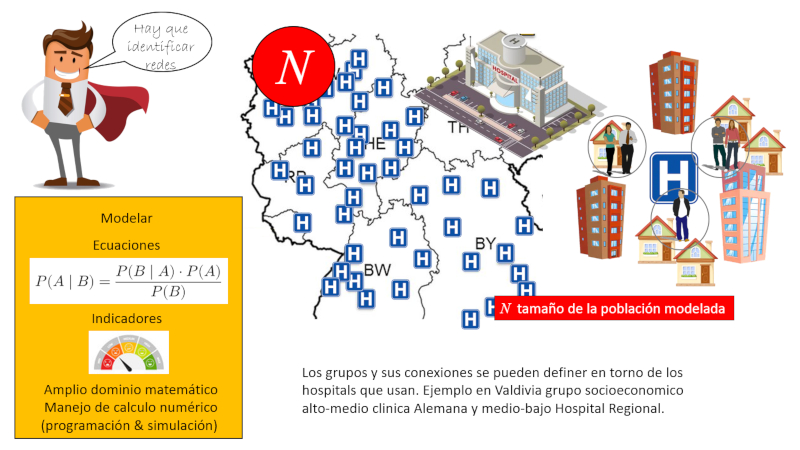
Tamaño de la comunidad
Imagen 
Una vez sabemos la probabilidad de contagiar debemos estimar el numero de infectados con los que nos contactamos y con ello tenemos la posibilidad de contagiarnos. Aquí debemos distinguir entre el numero de contactos diarios
En el caso de Valdivia se tiene aproximadamente unos 170 mil habitantes y dos clínicas con camas UTI (la Clínica Alemana y el Hospital Regional). En ese sentido se puede dividir Valdivia en dos grupos o comunidades que forma redes por la que se puede propagar la pandemia: la clase media a alta que tiende a usar los servicios de la Clínica Alemana y el segundo grupo que usa los servicios del Hospital Regional con un
ID:(11934, 0)
Número de infectados
Imagen 
Dentro de la comunidad con que habitualmente tenemos contactos están aquellas personas que en el momento están infectadas y en forma activa contagiando
Para estimar el numero de infectados activos es necesario medir osea diagnosticar la población. Esto puede hacerse tratando de cubrir la mayoría o vía muestreo y extrapolando a la comunidad completa. Por ello es necesario siempre saber el numero de testeo realizado de modo de que la proporción de caso positivos dividido por el numero de diagnósticos da una estimación del numero total de infectados. Por ello la frase que se escucha 'si se mide mas se encuentra mas y por ello no tiene sentido' ya que se debe siempre comprar el numero de positivos con el numero medido con lo que el aumento de mediciones solo aumenta la precisión.
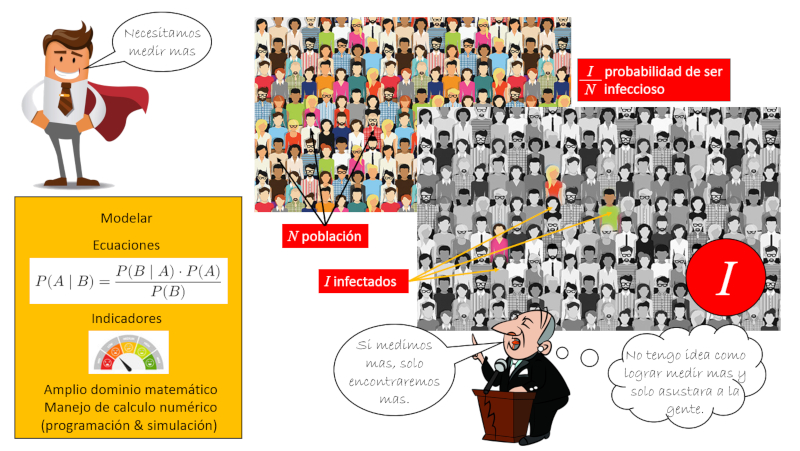
Nota: si se desea mantener bajo control un brote puede ser necesario buscar en forma sistemática los infectado para ponerlo bajo cuarentena. En estos casos la diagnostican de todas las personas y múltiple veces.
ID:(11933, 0)
Contactos diarios
Imagen 
Al día uno se reúne con un pequeños grupos de personas que denominamos contactos
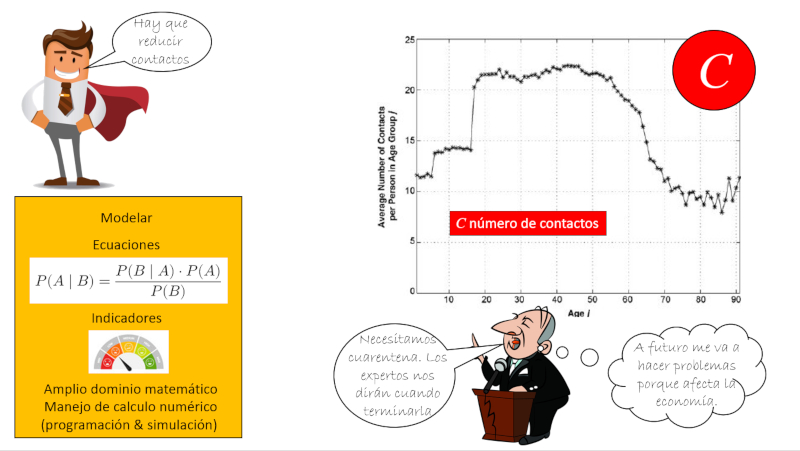
Grafica de 'Mixing patterns between age groups in social networks', S.Y. Del Valle a, J.M. Hyman b, H.W. Hethcote c, S.G. Eubank, Social Networks 29 (2007) 539-554
ID:(11935, 0)
Probabilidad de contagio diario
Imagen 
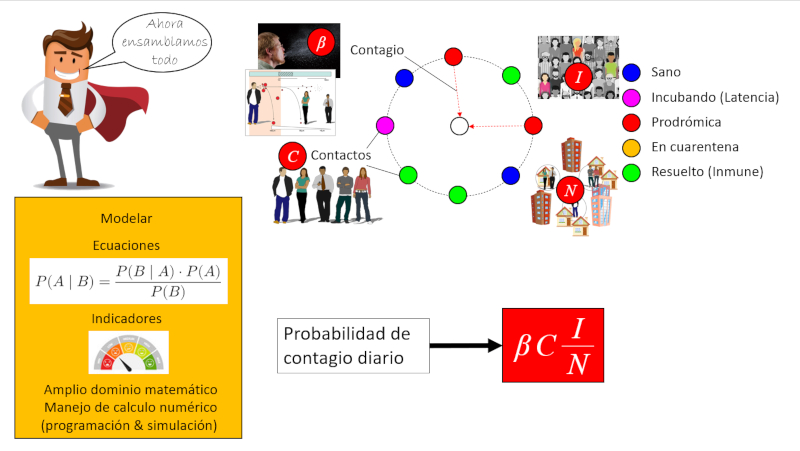
La probabilidad de que una persona se contagie se puede por ello estimar si se considera\\n\\n- todos los contactos C que se tiene por día\\n\\nSi se multiplica los contactos con la probabilidad de que una persona sea un contagiado activo
\beta C \displaystyle\frac{I}{N}
ID:(11936, 0)
Modelo SIR y su modificación
Imagen 
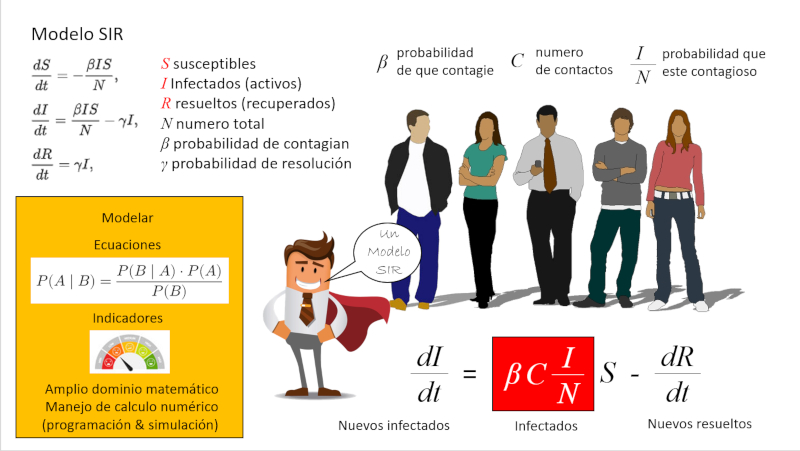
Para calcular la forma como se propaga la enfermedad podemos usar los modelos epidemiologicos del tipo SIR (susceptibles, infectados, recuperado o resuelto). En este se estima primero como varia el numero susceptibles
\displaystyle\frac{dS}{dt}=-\beta C\displaystyle\frac{I}{N} S
\\n\\nEl signo negativo refleja de que el numero susceptible se va reduciendo por efecto de la infección. En segundo lugar se debe considerar la población recuperada
\displaystyle\frac{dR}{dt}=\gamma I
\\n\\ncon lo que la variación de los infectados se calcula sumando los nuevos infectados y restando los resueltos\\n\\n
\displaystyle\frac{dI}{dt}=\beta C\displaystyle\frac{I}{N} S-\gamma I
\\n\\nEl problema en el modelo SIR es que los resueltos se sacas al azar de los infectados lo que no corresponde al proceso real en que existe una proceso de generación de síntomas, desarrollo de la enfermedad y finalmente recuperación o resolución con tiempos medios característicos. Por ello trabajaremos con una expresión alternativa\\n\\n
\displaystyle\frac{dI}{dt}=\beta C\displaystyle\frac{I}{N} S-\displaystyle\frac{dR}{dt}
ID:(11937, 0)
El problema en Chile
Imagen 
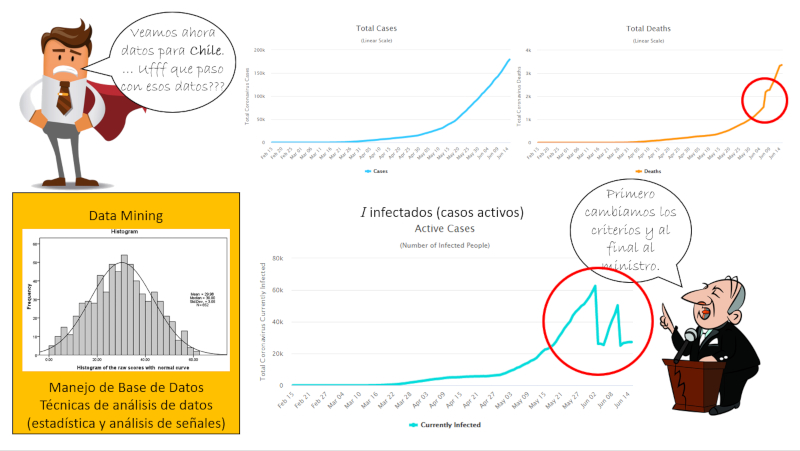
Si tratamos de aplicar el modelo para el caso chileno, vemos que los datos locales presenta anomalías graves:
• en los infectados diarios existen dos saltos que no pueden ser situación reales y de hecho si se estudia la información asociada se nota que en dos situación se cambio el criterio
• existe un salto de muertes adicionales que también proviene de un cambio de la fuente de información de datos compilados por hospitales al del registro civil
El problema de estos cambios se origino cuando Chile estudio los muertos en exceso o sea la cantidad de muertos que se observan este años con respecto de la tendencia que se tiene del año anterior. De ahí se determino que no se estaba registrando todos los muertos por COVID19 que estaban ocurriendo porque existían muertos que ocurría en las casas y no en los hospitales. Por ello se paso de reportes de hospitales a aquellos del registro civil. Por otro lado se reconoció de que había muerto por otras razones en que COVID19 había contribuido indirectamente. Con ello se ajusto los criterios para identificar los muertos.
El problema de estos cambios es que hace cuestionable la información histórica con lo que se pierde las condiciones iniciales en la solución de la ecuación del modelo a aplicar.
ID:(11938, 0)
La gravedad del problema
Imagen 
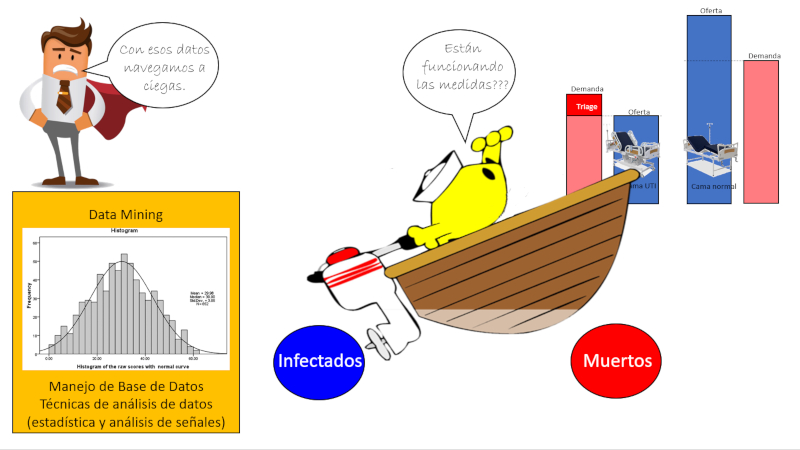
La gravedad de los problemas con los datos medios en Chile es que no permite estimar en forma confiable la necesidad hospitalaria que se presentara a futuro. En caso de no existir suficiente respiradores se llega a la situación en que hay que decidir a que paciente atender y aquel que literalmente hay que dejar morir por no existir suficiente infraestructura. En estos casos se evalúa la probabilidad de sobrevivencia y se da prioridad a los pacientes que tienen mejor pronostico (variante del tradicional triage).
El problema es que como la consecuencia de la infección se demora unos 14 días, toda acción que tomemos hoy se demorara este tiempo en tener efecto. Por ello es clave tener modelos que nos permitan evaluar de como la situación actual evolucionara frente a posible acciones que tomemos hoy de modo de seleccionar la que probablemente sea la mas adecuada.
Es como pilotear un bote desde una posición en la popa tratando de ver que la proa vaya por el camino correcto.
ID:(11939, 0)
Factor de reproducción
Imagen 
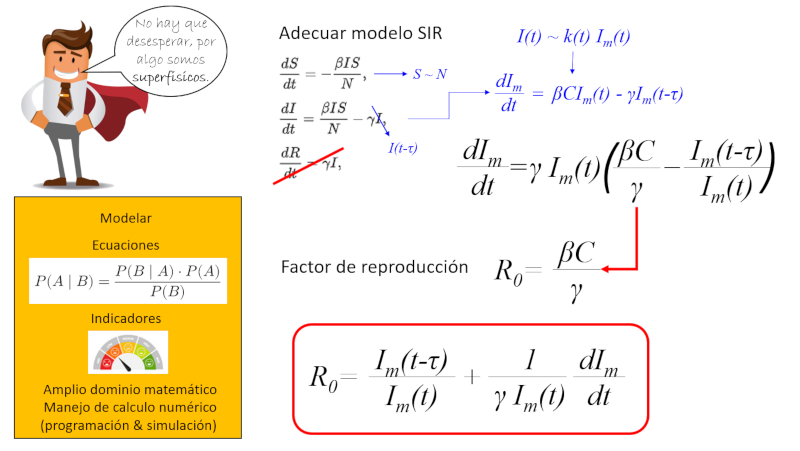
Desde la física se puede resolver la problemática. Como primer paso, con los muertos en exceso y los saltos de la curva se puede estimar un factor corrección
I(t) = k(t) I_m(t)
\\n\\nPor otro lado la reducción de infectado por resolución se puede estimar mediante el numero de infectados que reducimos hoy es similar a los infectados que se generaron hace un tiempo igual que la duración de la enfermedad. Como el tiempo de superar la enfermedad
\displaystyle\frac{dR}{dt} = \gamma I_m(t-\tau)
\\n\\nDe esta forma se puede reescribir la ecuación como\\n\\n
\displaystyle\frac{dI_m}{dt} = \gamma I_m(t)\left(\displaystyle\frac{\beta C}{\gamma}-\displaystyle\frac{I_m(t-\tau)}{I_m(t)}\right)
\\n\\nen donde se asumió que nos encontramos al comienzo de la pandemia y el numero de susceptible
S\sim N
\\n\\nEl factor\\n\\n
R_0=\displaystyle\frac{\beta C}{\gamma}
\\n\\nse denomina el factor de reproducción y caracteriza como se esta propagando la enfermedad dado que compara como se propaga
R_0=\displaystyle\frac{I_m(t-\tau)}{I_m(t)}+\displaystyle\frac{1}{\gamma I_m(t)}\displaystyle\frac{dI_m}{dt}
ID:(11940, 0)
Asociando comportamiento social y propagación del COVID19
Imagen 
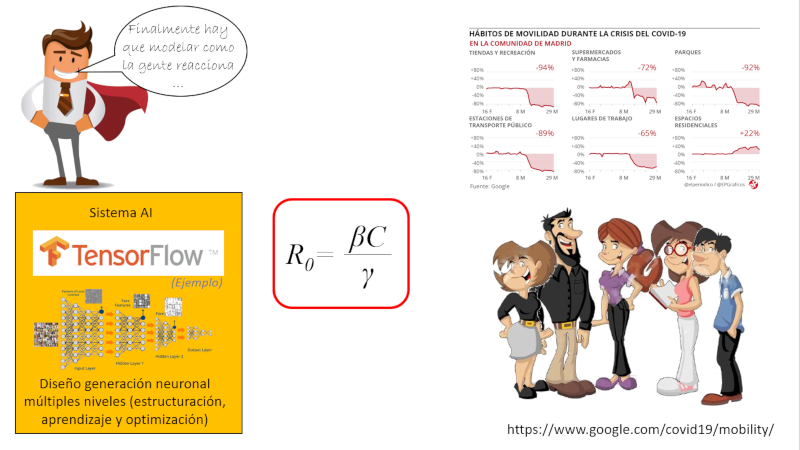
Una vez se tiene el factor de reproducción se puede asociar con factores que describen como los países reaccionaron a nivel de personas. Uno de los parámetros que permite hacer esto es los factores de movilidad que genera google y que muestra como el internet presenta menos búsquedas en algunos conceptos y mayor en otro.
Con un modelo de este tipo se puede cada vez desde el comportamiento de las personas inferir la propagación y con ello como se propaga y eventualmente se logra controlar la pandemia.
ID:(11941, 0)
Asociando medidas con comportamiento social
Imagen 
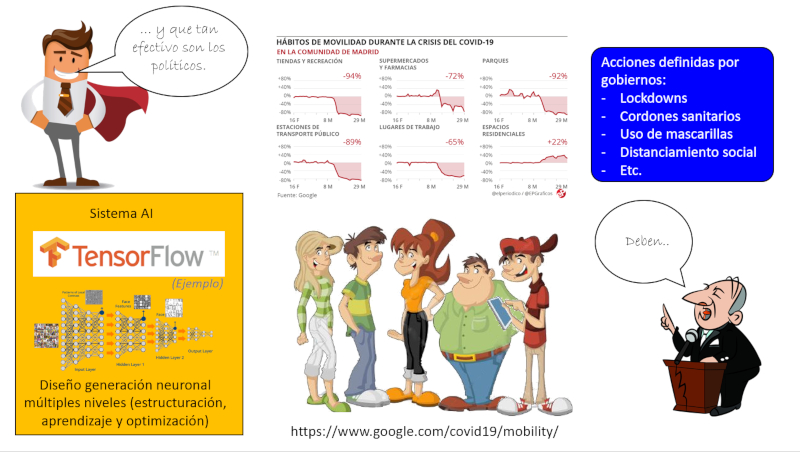
Una vez se tiene la relación entre como la comunidad se comporta y con ello como afecta la propagación de la pandemia se debe estudiar que tan efectivas son la medida de los gobiernos. Para ello se puede usar la información para construir un sistema de IA que nos entrega comportamiento ante acciones del gobiernos.
Con ello se tiene un sistema en que se puede usar para predecir como las acciones de los gobernantes influencia a las personas y como estas actúan en función de la propagación de la pandemia.
ID:(11942, 0)
Motivación final
Imagen 
Solo queda dejar tres mensajes para el camino:
• Sea curioso con datos. Cada vez que encuentra alguno, explore si contiene alguna información interesante. En particular vea si lo sorprende y habría esperado otro tipo de comportamiento. Si se da una discrepancia, a que se debe eso?, que supuso que no es tal?
• Cada vez que ve un proceso interesante piense como lo modelaría. Cuales variables usarías? Que relaciones asumirá?
• Programe. Conozca biblioteca que le permitan armar herramientas potentes con poco esfuerzo y tiempo. Como podría acceder a los datos en forma masiva? Con que algoritmo solucionaría los modelos con que trabaja? Como estructuraría un sistema de IA? como lo entrenaría? chequearías? y finalmente usaría'

ID:(11943, 0)
0
Video
Video: La Otra Física: métodos
