Zellularen Automaten
Bild 
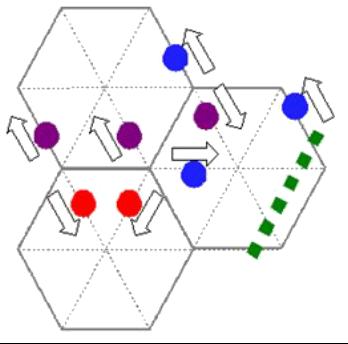
Die zellularen Automaten sind Modelle, die die Raumzeit diskretisieren und Automaten in jedem Punkt (Zelle) des Netzwerks definieren, die in der Funktion dessen arbeiten, was ihre Nachbarn tun (Automaten, weil sie eine definierte Form der Reaktion haben). Ein Beispiel ist eine sechseckige Struktur:
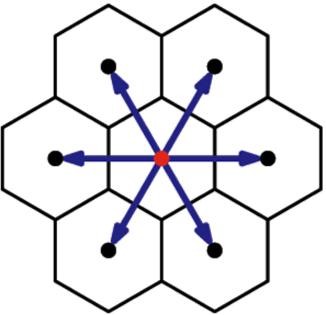
Modell D2Q7 (zwei Dimensionen und 7 Elemente pro Zelle - 6 Seiten und 1 Mitte)
Im Fall, dass es auf ein teilchenförmiges Gas angewendet wird, kann jeder Knoten (Zustände 0 und 1) ein Teilchen enthalten, das nur Geschwindigkeiten mit den Richtungen haben kann, die zwischen den Zellen verknüpfen.
In der Simulation mit Modellen wie zellularen Automaten gibt es zwei Phasen:
- Zelle wirkt auf die anderen
- Zelle verarbeitet Aktionen der Umwelt
Im speziellen Fall der Modellierung eines Gases entspricht der erste Schritt dem Fliessen (Streaming), während der zweite zur Kollision (Kollision).
Die mathematische Beschreibung erfolgt durch die Partikelverteilungsfunktion
| f_i(\vec{x},t)=w_if(\vec{x},\vec{v}_i,t) |
ID:(8494, 0)
D2Q9 Modelle (zweidimensionale, 9 Punkte)
Bild 
El modelo D2Q9 es un modelo bidimensional (D2) en que se se conecta el nodo (punto central) en nodos a lo largo de los ejes cartesianos\\n\\nen el origen\\n\\n
\vec{e}_0=(0,0)
\\n\\nen las esquinas\\n\\n
\vec{e}_1=(1,0)
(E),\\n
\vec{e}_2=(0,1)
(N), \\n
\vec{e}_3=(-1,0)
(W) y \\n
\vec{e}_4=(0,-1)
(S)\\n\\ny en las diagonales\\n\\n
\vec{e}_5=(1,1)
(NE), \\n
\vec{e}_6=(-1,1)
(SE), \\n
\vec{e}_7=(-1,-1)
(SW) y \\n
\vec{e}_8=(1,-1)
(NW)
lo que se representa en la siguiente gráfica:
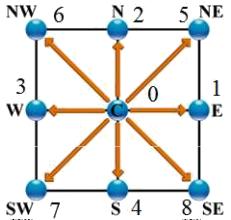
ID:(8496, 0)
Distribuciones D2Q9 (2 dimensiones, 9 puntos)
Gleichung 
El modelo D2Q9 la distribución en equilibrio se describe mediante la ecuación
| f_i^{eq}=\rho\omega_i\left[1+3\vec{e}_i\cdot\vec{u}+\displaystyle\frac{9}{2}(\vec{e}_i\cdot\vec{u})^2-\displaystyle\frac{3}{2}\mid\vec{u}|^2\right] |
\\n\\nen donde los pesos de la probabilidad son\\n\\n
\omega_0=\displaystyle\frac{4}{9}
\\n\\n
\omega_1=\omega_2=\omega_3=\omega_4=\displaystyle\frac{1}{9}
\\n\\n
\omega_5=\omega_6=\omega_7=\omega_8=\displaystyle\frac{1}{36}
ID:(8705, 0)
Calculo nueva Distribuciones D2Q9
Gleichung 
El modelo D2Q9 la distribución se recalcula por efecto de las colisiones mediante
| f_i^{new}=f_i^{old}+\displaystyle\frac{1}{\tau}(f_i^{eq}-f_i^{old}) |
ID:(8706, 0)
D3Q15 Modelle (dreidimensionale, 15 Punkte)
Bild 
Das D3Q15 Modell ist ein zweidimensionales Modell (D3), in dem der Knoten (Punkt center) Knoten entlang der kartesischen Achsen verbindet\\n\\n
(1,0,0), (-1,0,0), (0,1,0), (0,-1,0), (0,0,1) (0,0,-1)
\\n\\nund in den Ecken des Würfels\\n\\n
(1,0,1), (-1,0,1), (0,1,1) , (0,-1,1), (1,0,-1), (-1,0,-1), (0,1,-1) , (0,-1,-1)
was es in der folgenden Grafik dargestellt ist:
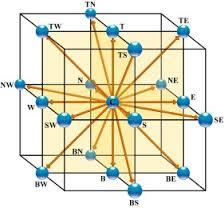
Es ist relativ einfach Modelle zu bauen vom Typ D3Q19 (einschließlich der Hälften der Seitenkanten ) oder D3Q27 (alle möglichen Punkte).
ID:(8497, 0)
Streaming
Bild 
En la etapa de steraming (flujo) se transportan las partículas de una celda según la dirección de la velocidad que tengan hacia el nodo correspondiente:
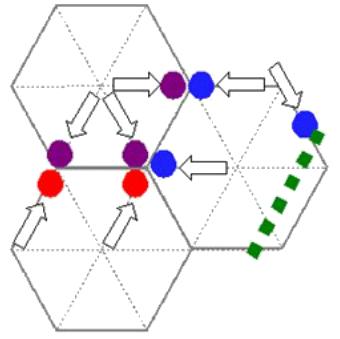
\\n\\nEn el caso del streaming se re calculan las funciones distribución en el sentido de que se re calculan sus componentes:\\n\\n
f_i(\vec{x}+\vec{e}_i\delta t,t+\delta t)=f_i(\vec{x},t)
En este punto también se incluye el efecto de los bordes que en el caso estático reflejan la velocidad (rebote) y en el caso que se estén moviendo la modifican.
ID:(8498, 0)
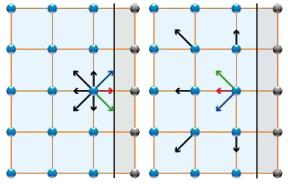
Collision
Bild 
En la etapa de colisiones se reasignan partículas de una dirección de velocidad a otra:
\\n\\nPara ello es necesario modelar la colisión que finalmente depende de la distribución misma y del tipo de interacción que exista. El resultado es que la nueva función distribución será:\\n\\n
f_i(\vec{x},t+\delta t)=f_i(\vec{x},t)+C(f)
ID:(8495, 0)
Borde simple
Bild 
El borde mas simple es una pared paralela a la red misma de modo que las partículas pueden rebotar en forma simple:
\\n\\nEn estos casos la función distribución se deja fácilmente calcular simplemente invirtiendo la velocidad en la distribución en la posición simétrica al punto de rebote:\\n\\n
f(\vec{x},e_i,t+\delta t)=f(\vec{x},-e_i,t)
ID:(8501, 0)
Rückprall in Wänden orthogonal zu dem Netzwerk
Bild 
Wenn der Rückprall nicht an einem Punkt des Netzes sondern in einem Abstand
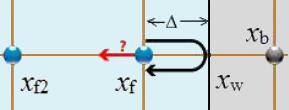
\\n\\ndann sollte die Funktion die Beiträge der Abweichungen berücksichtigen\\n\\n
f_i(x_f,t+\delta t)=\displaystyle\frac{(1-\Delta)f_{-i}(x_f,t)+\Delta(f_{-i}(x_b,t)+f_{-i}(x_{f2},t)}{1+\Delta}
ID:(8499, 0)
Rückprall bei geneigte Wände
Bild 
Wenn die Wand eine Neigung haben bezüglich des Netzwerk es in einer komplexere Modellierung notwendig:
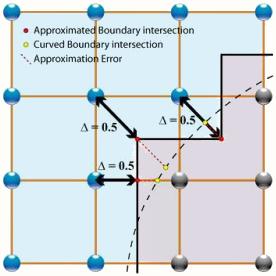
Allgemeine Umrandung
Zunächst muss eine ungefähre Grenze festgelegt werden um dann die entsprechende Gleichungen definiert werden. Diese wird dann innerhalb des Streamng Prozess angewandt.
ID:(8500, 0)
Rebote en paredes con Angulo
Beschreibung 
Si la pare se encuentra en movimiento a una velocidad \vec{U} debe considerarse que puede incrementar o frenar a las partículas. En general se tendrá que\\n\\n
f_i(\vec{e}_i,t+\delta t)=f_{-i}(\vec{e}_i)+G(\vec{e}_i,\vec{U})+G(-\vec{e}_i,-\vec{U})
\\n\\nque se puede simplificar a \\n\\n
f_i(e_i,t+\delta t)=f_{-i}(e_i)+\displaystyle\frac{6}{c^2}(\omega_im\vec{U}\cdot\vec{e}_i)
ID:(8502, 0)
