Changes in albedo
Storyboard 
The variation of the albedos is based on the variation of their own surfaces. In this sense, the total albedo can increase or decrease as long as low albedo surfaces become high albedo or vice versa. Typical examples are, for example, afforestation in which an area with vegetation (albedo of the order of 0.15) passes to have scarce vegetation (albedo of the order of 0.30). A reverse example occurs with the melting of glaciers (albedo of the order of 0.6) become deforested areas (0.30) or ocean (albedo of the order of 0.06).
ID:(577, 0)
Albedo of the earth\'s surface
Description 
Albedo is a measure of the reflectivity of a surface, that is, the amount of solar radiation that is reflected by that surface. Different types of soils, coverings, and vegetation have different reflective properties, resulting in variations in albedo.
For example, surfaces covered in snow tend to have a high albedo because snow is highly reflective and reflects a large amount of solar radiation. On the other hand, areas with dense vegetation may have a lower albedo as plants absorb some of the solar radiation for photosynthesis.
Additionally, the state of vegetation can also influence albedo. During the growing season, when plants are in full foliage, the albedo may be lower due to higher absorption of solar radiation. However, during times of drought or when leaves fall in autumn, the albedo can increase due to reduced absorption of radiation.
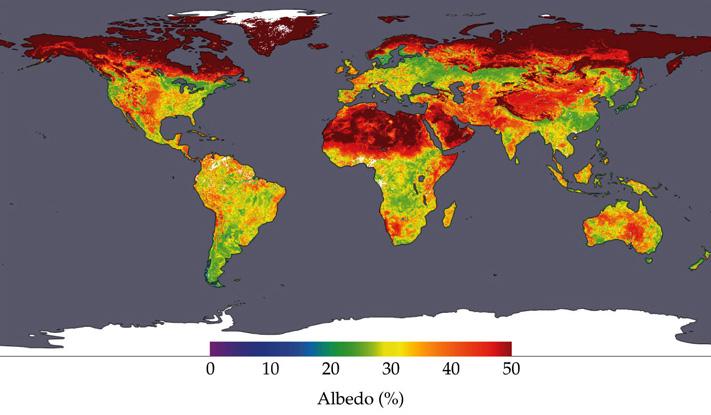
Albedo de la Superficie
ID:(7329, 0)
Albedo variations
Equation 
The Earth\'s albedo, represented by the symbol \alpha, is the fraction of solar radiation reflected by the Earth. Changes in albedo can have a significant impact on the Earth\'s energy balance and global climate. Factors such as cloud cover, ice, vegetation, and land surface influence the albedo.
By modifying the Earth\'s albedo, either through natural changes or human activities, the amount of solar radiation absorbed or reflected by the Earth can be altered, thereby affecting the climate and climate patterns. It is important to understand and monitor these changes in albedo to assess their impact on the climate system and global temperature.
These variations will occur based on changes in albedo and coverage factors:
a_e\rightarrow a_e + \delta a_e
Therefore, the new Earth\'s albedo will be:
ID:(88, 0)
Suma de Superficies de la Tierra
Equation 
Las superficies total terrestre S_i se obtiene de las suma de las superficies individuales
S_e=\sum_iS_{e,i}
ID:(7501, 0)
Calculo del Albedo Terrestre
Equation 
Si la superficie del planeta esta compuesta de zonas si con albedo ai, el albedo total sera
a_e =\displaystyle\frac{\sum_is_ia_{e,i}}{\sum_is_i}
ID:(7438, 0)
Variación de la Superficie de la Tierra
Equation 
La variación de la superficies total terrestre debe ser nula si la superficie se conserva:
\sum_i\delta S_{e,i}=0
ID:(7503, 0)
Calculation of terrestrial albedo variations
Equation 
The variation in the albedo of Earth\'s surface is due to changes in its composition and characteristics. For example, forests can be deforested, resulting in a decrease in albedo due to the exposure of dark soil. Conversely, areas can be reforested, increasing the albedo by reintroducing vegetation. Additionally, the albedo can vary due to the accumulation or melting of snow, which creates areas with different albedos.
If we consider that the planet\'s surface is composed of different zones, each with a specific albedo denoted as a_i, then the total albedo is calculated by summing the contribution of each zone. This can be expressed using the following equation:
| a_e =\displaystyle\sum_i s_{e,i} a_{e,i} |
Where the summation is performed over all the zones present on the Earth\'s surface.
The variation in the surface with a particular albedo leads to changes in the fractions of the different zones. This implies that changes in the surface affect the proportion of each zone relative to the total area. This relationship can be expressed using the following equation:
Where a_i represents the albedo of zone i, and the summation is performed over all the zones present.
The variation in the total albedo due to changes in the surface can be calculated using Kyon, which represents the relative difference between two albedo values:
It is important to note that these equations are general and simplified representations of the phenomena related to the variation in Earth\'s surface albedo. The reality is much more complex, as multiple factors and processes influence the albedo, such as the presence of clouds, atmospheric aerosols, and other elements.
ID:(7320, 0)
